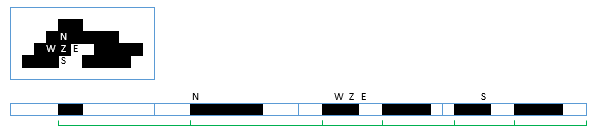
Контур цифровой формы с длиной серий
Цифровая форма - это набор связанных пикселей в двоичном изображении (BLOB-объект).
Он может быть компактно представлен с помощью кодирования длин серий, то есть группировки пикселей по горизонтальным отрезкам и сохранения координат начальной конечной точки и длин. Обычно представление RLC хранит прогоны в растровом порядке, то есть строка за строкой и направленная вправо.
Для гладких форм требования к хранению снижаются с O(N²) до O(N).
Контур фигуры представляет собой замкнутую цепочку пикселей, которая восстанавливает фигуру, когда ее внутренняя часть заполнена (с помощью алгоритма заливки). Это также O (N) представление. Когда форма доступна в виде растрового изображения, контур может быть получен с помощью контурного алгоритма.
Я ищу алгоритм, который непосредственно вычисляет контур фигуры с учетом ее представления RLC, не рисуя его в промежуточном растровом изображении. Ожидается, что алгоритм будет работать во времени, линейном по количеству прогонов.
Вы сталкивались с решением?
3 ответа
Пиксель - это граничный пиксель, если он заполнен, но примыкает к пикселю, который не заполнен. Учитывая RLE-кодирование для каждой строки заполненных пикселей, мы можем работать с тремя смежными строками, чтобы вычислить RLE-версию граничных пикселей, а затем декодировать ее.
По сути, у нас есть алгоритм стреловидности. С тремя рядами, как
*********** ****
************************
**** ******
мы получаем очки событий (^) из РЛЭ:
*********** ****
************************
**** ******
^ ^^ ^ ^ ^ ^^ ^
Первое, что нужно сделать, это обозначить пиксели со средним заполнением, у которых пустые пиксели выше или ниже, в качестве границы. (Если вам нужно руководство, алгоритмы для установки разности в списке интервалов очень похожи.)
*********** ****
BBB***BBBBBBBBBBB***BBBB
**** ******
Затем для интервалов, которые заполнены, но не известны как границы, проверьте, имеет ли левая конечная точка место слева и есть ли у правой конечной точки пространство справа. Если так (соответственно), они границы.
Подсказка:
Как сказано в других ответах, выдача списка пикселей контура может быть реализована как процесс развертки, во время которого исследуются окрестности 3х3 конечных точек прогона.
Эта процедура будет излучать пиксели в зашифрованном виде в виде последовательности прямых и обратных дуг, которые необходимо сохранить и переупорядочить.
Альтернатива может быть основана на идее реализации стандартного алгоритма Соседства Мура, который имеет преимущество для перечисления контурных пикселей в желаемом порядке.
Для этой процедуры требуется знать конфигурацию с 8 соседями вокруг текущего пикселя, и идея состоит в том, чтобы обновлять эту окрестность при каждом перемещении к другому пикселю: мы поддерживаем индексы для прогона, который содержит текущий пиксель, и для двух встречных трасс в строках над и под.
При каждом переходе к другому пикселю нам нужно обновлять эти три индекса, что будет включать короткие последовательные поиски в списке отсортированных прогонов. Это можно рассматривать как механизм псевдослучайного доступа к пикселям, принимая во внимание, что последовательные обращения строго локальны и могут быть как бы кэшированы.
Обновление:
В представлении с кодированием длины серии, которое я использую, только черные серии кодируются как тройки (X, Y, L), Трассы сортируются по строкам сверху вниз, а затем слева направо подряд.
Для удобства мы можем переключиться на схему "линейной адресации", как если бы все строки изображения были добавлены друг за другом, и каждый пиксель обозначен одним числом Z = X + Y.Nx (где Nx ширина изображения).
Таким образом, у нас есть список черных трасс, и белые трассы неявно находятся между двумя последовательными черными.
Во время обработки мы можем всегда помнить индекс запуска, который начинается непосредственно перед или на текущем пикселе (R[I].Z <= Z < R[I+1].Z). Мы можем определить цвет пикселя, проверив, находимся ли мы внутри пробега или между ним и следующим (Z < R[I].Z + R[I].L).
Если мы переместимся на одну позицию влево, Z уменьшается на 1 и нам, возможно, придется выбрать предыдущий прогон (I--).
Если мы переместимся на одну позицию вверх, Z уменьшается на Nx и нам, возможно, придется вернуться на несколько прогонов (I-- до тех пор R[I].Z <= Z снова).
На рисунке показан текущий пиксель и его 4-х соседей, а также "зоны влияния" черных трасс. Мы можем обрабатывать все восемь направлений смещения одинаково.
Как мы видим, каждое движение требует в худшем случае количества операций, равного количеству прогонов подряд, что считается небольшим значением. Используя эту концепцию, мы можем пройти представление RLC по произвольному пути по разумной цене, не восстанавливая всю битовую карту.
Поскольку алгоритм Соседства Мура занимает время, линейное по длине контура, реализация, основанная на этой линейной адресации прогонов, также потребует линейного времени (для ограниченного числа прогонов в строке).
Примечание. В этом ответе предполагается, что "не очерченный" означает "окруженный 4 соседями", поэтому результат будет немного отличаться от вашего примера (1 пиксель зеленого цвета вместо синего).
Все контурные пиксели являются пикселями, в которых установлены не все 4 "соседних пикселя" (слева, справа, сверху, снизу от пикселя).
При декодировании RLC сверху вниз вы можете получить контурные пиксели с помощью следующего алгоритма псевдокода:
For the first line
All decoded pixels are outline pixels
For the subsequent lines
Leftmost and rightmost pixels of each RLC run are outline pixels
All other pixels are outline pixels if:
The pixel above isn't set (case A)
The pixel below isn't set (case B)
Случаи A и B означают, что вам придется смотреть на пиксели выше / ниже текущего пикселя, поэтому алгоритм должен быть отчасти конвейерным / смотреть вперед на одну строку, потому что случай B не сможет быть обнаружен до следующей строки был расшифрован.
РЕДАКТИРОВАТЬ: для сортировки пикселей по часовой стрелке впоследствии, вы можете использовать тот факт, что ваш контур представляет собой диагонально соединенную линию шириной в один пиксель. Выбрав один из пикселей в верхней строке, у вас будет два возможных следующих пикселя, следуйте за тем, который справа, ниже или справа и ниже текущего пикселя. После этого просто следите за соседними пикселями, которые вы еще не посетили, пока не будет соседнего пикселя. Пример:
/----- First pixel you pick, A and B are neighbour candidates, A is the "correct" one
v
xAxxx
B x
x x xxx
x xxxxxx x
xx x
xxxxxxxxxxx
s0123 Result after following the neighbours (s = start, e = end),
e 4 numbers from 0-9 show order of traversal
1 5 234
0 678901 5
98 6
76543210987