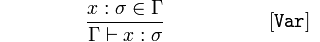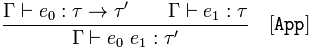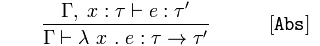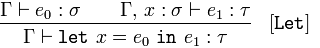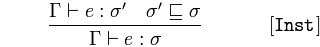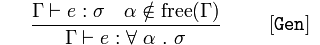"Какую часть Хиндли-Мильнера ты не понимаешь?"
Клянусь, раньше продавалась футболка с бессмертными словами:
Какая часть
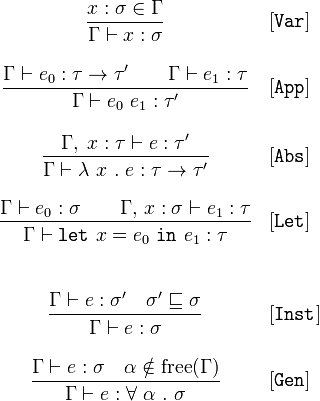
ты не понимаешь?
В моем случае ответ будет... все это!
В частности, я часто вижу подобные обозначения в документах на Haskell, но я понятия не имею, что это означает. Я понятия не имею, какой отраслью математики она должна быть.
Разумеется, я распознаю буквы греческого алфавита и такие символы, как "∉" (что обычно означает, что что-то не является элементом набора).
С другой стороны, я никогда раньше не видел "⊢" ( Википедия утверждает, что это может означать "раздел"). Я также незнаком с использованием винкулюма здесь. (Обычно это обозначает дробь, но здесь это не так.)
Если кто-нибудь хотя бы скажет мне, с чего начать, чтобы понять, что означает это море символов, это было бы полезно.
6 ответов
- Горизонтальная полоса означает, что "[выше] подразумевает [ниже]".
- Если в [выше] есть несколько выражений, то рассмотрите их как объединенные; все [выше] должно быть верно, чтобы гарантировать [ниже].
:значит имеет тип∈значит в. (Точно так же∉означает "не в".)Γобычно используется для обозначения среды или контекста; в этом случае его можно рассматривать как набор аннотаций типов, связывающих идентификатор с его типом. Следовательноx : σ ∈ Γозначает, что средаΓвключает в себя тот факт, чтоxимеет типσ,⊢может быть прочитано как доказывает или определяет.Γ ⊢ x : σозначает, что средаΓопределяет, чтоxимеет типσ,,это способ включения конкретных дополнительных допущений в окружающую средуΓ,
Следовательно,Γ, x : τ ⊢ e : τ'означает, что средаΓс дополнительным, преобладающим предположением, чтоxимеет типτ, доказывает чтоeимеет типτ',
По запросу: приоритет оператора, от высшего к низшему:
- Специфичные для языка операторы инфикса и миксфикса, такие как
λ x . e,∀ α . σ, а такжеτ → τ',let x = e0 in e1и пробелы для применения функции. :∈а также∉,(Левоассоциативные)⊢- пробел, разделяющий несколько предложений (ассоциативный)
- турник
Этот синтаксис, хотя и может показаться сложным, на самом деле довольно прост. Основная идея исходит из формальной логики: все выражение является следствием, причем верхняя половина является предположениями, а нижняя половина - результатом. То есть, если вы знаете, что верхние выражения верны, вы можете сделать вывод, что нижние выражения также верны.
Символы
Следует также помнить, что некоторые буквы имеют традиционное значение; в частности, Γ представляет "контекст", в котором вы находитесь, то есть типы других вещей, которые вы видели. Так что-то вроде Γ ⊢ ... означает "выражение ... когда вы знаете типы каждого выражения в Γ,
⊢ Символ по сути означает, что вы можете что-то доказать. Так Γ ⊢ ... это утверждение, говорящее "Я могу доказать ... в контексте Γ, Эти утверждения также называются суждениями типа.
Еще одна вещь, которую нужно иметь в виду: в математике, как ML и Scala, x : σ Значит это x имеет тип σ, Вы можете прочитать это так же, как у Хаскелла x :: σ,
Что означает каждое правило
Итак, зная это, первое выражение становится легко понять: если мы знаем, что x : σ ∈ Γ (то есть, x имеет какой-то тип σ в каком-то контексте Γ), то мы знаем, что Γ ⊢ x : σ (то есть в Γ, x имеет тип σ). Так что на самом деле, это не говорит вам ничего супер-интересного; это просто говорит вам, как использовать ваш контекст.
Другие правила также просты. Например, взять [App], Это правило имеет два условия: e₀ это функция из некоторого типа τ к какому-то типу τ' а также e₁ это значение типа τ, Теперь вы знаете, какой тип вы получите, подав заявку e₀ в e₁! Надеюсь, это не удивительно:).
Следующее правило имеет еще один новый синтаксис. В частности, Γ, x : τ просто означает, что контекст состоит из Γ и суждение x : τ, Итак, если мы знаем, что переменная x имеет тип τ и выражение e имеет тип τ'мы также знаем тип функции, которая принимает x и возвращается e, Это просто говорит нам, что делать, если мы выяснили, какой тип принимает функция и какой тип она возвращает, поэтому это тоже не должно удивлять.
Следующий просто говорит вам, как справиться let заявления. Если вы знаете, что какое-то выражение e₁ имеет тип τ пока x имеет тип σ, затем let выражение, которое локально связывает x к значению типа σ сделаю e₁ иметь тип τ, На самом деле, это просто говорит о том, что оператор let по существу позволяет расширять контекст с помощью новой привязки, а это именно то, что let делает!
[Inst] правило имеет дело с подтипом. Это говорит о том, что если у вас есть значение типа σ' и это подтип σ (⊑ представляет отношение частичного порядка), то это выражение также имеет тип σ,
Последнее правило касается обобщающих типов. Небольшое отступление: свободная переменная - это переменная, которая не вводится оператором let или лямбда-выражением внутри некоторого выражения; это выражение теперь зависит от значения свободной переменной из ее контекста. Правило гласит, что если есть какая-то переменная α который не является "свободным" ни в чем в вашем контексте, тогда можно с уверенностью сказать, что любое выражение, тип которого вы знаете e : σ будет иметь этот тип для любого значения α,
Как пользоваться правилами
Итак, теперь, когда вы понимаете символы, что вы делаете с этими правилами? Ну, вы можете использовать эти правила, чтобы выяснить тип различных значений. Чтобы сделать это, посмотрите на ваше выражение (скажем, f x y) и найдите правило, в котором есть заключение (нижняя часть), соответствующее вашему утверждению. Давайте назовем то, что вы пытаетесь найти своей "целью". В этом случае вы бы посмотрели на правило, которое заканчивается в e₀ e₁, Когда вы нашли это, теперь вы должны найти правила, доказывающие все, что находится выше линии этого правила. Эти вещи, как правило, соответствуют типам подвыражений, так что вы по существу повторяете части выражения. Вы просто делаете это, пока не закончите свое дерево доказательств, которое дает вам подтверждение типа вашего выражения.
Таким образом, все эти правила указывают точно - и в обычной математически педантичной детализации:P - как выяснить типы выражений.
Теперь, это должно звучать знакомо, если вы когда-либо использовали Пролог - вы по сути вычисляете дерево доказательств, как человеческий интерпретатор Пролога. Есть причина, по которой Пролог называют "логическим программированием"! Это также важно, так как я впервые познакомился с алгоритмом логического вывода HM, реализовав его в Прологе. Это на самом деле удивительно просто и проясняет происходящее. Вы должны обязательно попробовать это.
Примечание: я, вероятно, допустил некоторые ошибки в этом объяснении и был бы рад, если бы кто-то на них указал. На самом деле я расскажу об этом в классе через пару недель, поэтому я буду более уверенным в этом:P.
если бы кто-нибудь мог хотя бы сказать мне, где начать искать, чтобы понять, что означает это море символов
См. " Практические основы языков программирования ", главы 2 и 3, о стиле логики через суждения и выводы. Вся книга теперь доступна на Amazon.
Глава 2
Индуктивные определения
Индуктивные определения являются незаменимым инструментом в изучении языков программирования. В этой главе мы разработаем основные рамки индуктивных определений и приведем несколько примеров их использования. Индуктивное определение состоит из набора правил для выведения суждений или утверждений различных форм. Суждения - это утверждения об одном или нескольких синтаксических объектах указанного вида. Правила определяют необходимые и достаточные условия для действительности решения и, следовательно, полностью определяют его значение.
2.1 Суждения
Мы начнем с понятия суждения или утверждения о синтаксическом объекте. Мы будем использовать многие формы суждения, включая такие примеры:
- n nat - n натуральное число
- n = n1 + n2 - n это сумма n1 и n2
- тип τ - тип τ
- e: τ - выражение e имеет тип τ
- e ⇓ v - выражение e имеет значение v
Суждение гласит, что один или несколько синтаксических объектов имеют свойство или стоят в некотором отношении друг к другу. Само свойство или отношение называется формой суждения, а суждение о том, что объект или объекты обладают этим свойством или позицией в этом отношении, называется экземпляром этой формы суждения. Форма суждения также называется предикатом, а объекты, составляющие экземпляр, являются его субъектами. Мы пишем J для суждения, утверждающего, что J держит a. Когда не важно подчеркнуть предмет решения (текст обрывается здесь)
Как я понимаю правила Хиндли-Милнера?
Хиндли-Милнер - это набор правил в форме последовательного исчисления (не естественного вычитания), который говорит, что вы можете вывести (наиболее общий) тип программы из конструкции программы без явных объявлений типов.
Символы и обозначения
Во-первых, давайте объясним символы
- это идентификатор (неофициально, имя переменной).
- : средство - это тип (неофициально, экземпляр или "is-a").
- (сигма) - это выражение, которое является либо переменной, либо функцией.
- ∈ означает элемент
- (Гамма) это среда.
- ⊦ (знак утверждения) означает, что утверждает (или доказывает, но в контексте "утверждает" читается лучше.)
- ⊦ : Таким образом, читает утверждает,
- фактический экземпляр (элемент) типа ,
- (Тау) является типом: либо основной, переменная (), функциональный → ', или продукт ×'
- → ' - это функциональный тип, где и ' являются типами.
- , средства (лямбда) является анонимной функцией, которая принимает аргумент, и возвращает выражение, ,
- позволять = ₀ в ₁ означает в выражении, ₁, заменить ₀ где бы появляется.
- ⊑ означает, что предыдущий элемент является подтипом (неофициально - подклассом) последнего элемента.
- переменная типа
- ∀ . является типом, ∀ (для всех) переменных аргумента, , возвращаясь выражение
- ∉ free () означает не элемент переменных свободного типа, определенных во внешнем контексте. (Связанные переменные являются заменяемыми.)
Все выше линии - предпосылка, все ниже - заключение ( Пер Мартин-Лёф)
Далее следует английская интерпретация логических утверждений с последующим объяснением.
переменная
Данный тип (сигма), элемент (гамма),
Заключить утверждает, что.
Это в основном тавтология - имя идентификатора - это переменная или функция.
Применение функции
Данные утверждения ₀ являются функциональным типом, а утверждения ₁ являются
сделать вывод, применяя функцию ₀ к ₁ типу
Это означает, что если мы знаем, что функция возвращает тип, и мы применяем его к аргументу, результатом будет экземпляр типа, который мы знаем, что он возвращает.
Функция Абстракция
Данный и типа утверждает, является типом, '
В заключении утверждается, что анонимная функция с возвращаемым выражением имеет тип →'.
Это означает, что если мы знаем, что это тип и, следовательно, выражение имеет тип ', то функция возвращающего выражения имеет тип →'.
Пусть объявление переменной
Даны утверждения ₀ типа и, и, типа, утверждения ₁ типа
сделать выводlet= ₀in₁ типа
Это означает, что если у нас есть выражение ₀, которое является (являющимся переменной или функцией), и какое-то имя, также a, и выражение type типа, то мы можем заменить ₀ на то, где оно появляется внутри ₁.
Конкретизация
Данные утверждения типа 'и' являются подтипом
сделать вывод, что имеет тип
Это говорит о том, что если экземпляр имеет тип, который является подтипом другого типа, он также является экземпляром этого супертипа.
Это позволяет нам использовать создание экземпляров в более общем смысле, что выражение может возвращать более конкретный тип.
Обобщение
Данные утверждения являются и не являются элементом свободных переменных
завершение утверждает, введите для всех аргументов выражений, возвращающих выражение
Это означает, что мы можем обобщить программу, чтобы она принимала все типы для аргументов, которые еще не связаны в содержащей области (переменные, которые не являются нелокальными). Эти связанные переменные являются заменяемыми.
Заключение
Объединение этих правил позволяет нам доказать наиболее общий тип утвержденной программы, не требуя аннотаций типов, что позволяет правильно принимать различные типы в качестве входных данных (параметрический полиморфизм).
Обозначение происходит от естественного вывода.
⊢ символ называется турникет.
6 правил очень просты.
Var Правило является довольно тривиальным правилом - оно говорит, что если тип для идентификатора уже присутствует в вашей среде типов, то для вывода типа вы просто берете его из среды как есть.
App Правило гласит, что если у вас есть два идентификатора e0 а также e1 и можете вывести их типы, то вы можете сделать вывод о типе приложения e0 e1, Правило звучит так, если вы знаете, что e0 :: t0 -> t1 а также e1 :: t0 (то же самое t0!), тогда приложение хорошо напечатано и тип t1,
Abs а также Let являются правилами для вывода типов для лямбда-абстракции и ввода.
Inst Правило говорит, что вы можете заменить тип на менее общий.
Есть два способа думать о е: σ. Одним из них является "выражение e имеет тип σ", другим является "упорядоченная пара выражения e и тип σ".
Рассматривайте Γ как знания о типах выражений, реализованные как набор пар выражений и типов, e: σ.
Турникет ⊢ означает, что из знания слева мы можем сделать вывод, что справа.
Таким образом, первое правило [Var] можно прочитать:
Если наше знание Γ содержит пару e: σ, то мы можем вывести из Γ, что e имеет тип σ.
Второе правило [App] можно прочитать:
Если мы из Γ можем вывести, что e_0 имеет тип τ → τ', и мы из Γ можем вывести, что e_1 имеет тип τ, то мы из Γ можем сделать вывод, что e_0 e_1 имеет тип τ'.
Обычно пишут Γ, e: σ вместо Γ ∪ {e: σ}.
Таким образом, третье правило [Abs] можно прочитать:
Если мы из Γ, расширенного с помощью x: τ, можем вывести, что e имеет тип τ ', то мы из Γ можем сделать вывод, что λx.e имеет тип τ → τ'.
Четвертое правило [Позвольте] оставлено в качестве упражнения.:-)
Пятое правило [Inst] можно прочитать:
Если мы из Γ можем вывести, что e имеет тип σ', а σ' является подтипом σ, то мы из Γ можем вывести, что e имеет тип σ.
Шестое и последнее правило [Gen] можно прочитать:
Если мы из Γ можем вывести, что e имеет тип σ, и α не является переменной свободного типа ни в одном из типов в Γ, то мы из Γ можем сделать вывод, что e имеет тип ∀α σ.