Когда пространство гипотезы содержит целевую концепцию

Question

Что это означает, когда написано, что пространство гипотез содержит целевое понятие? Если возможно с примером.

Answer 1

TLDR: это означает, что вы можете учиться без ошибок.

---

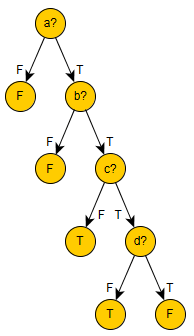
Вот пример того, что это значит: Предположим, концепция: f(a,b,c,d) = a & b & (!c | !d) (входные данные находятся в логическом домене).

Эта концепция в задаче ML обычно представлена ​​данными, поэтому вы получаете набор данных:

a | b | c | d = f
--+---+---+---+---
T   T   T   T = F
T   T   T   F = T
T   T   F   T = T
   ... etc ...

И ваша гипотеза пространства - деревья решений. В этом случае ваше пространство гипотез содержит целевую концепцию, как вы можете сделать (например, есть больше возможностей):

Можно доказать, что любая двоичная формула (концепция) может быть изучена как дерево решений. Таким образом, общие двоичные формулы являются подмножеством деревьев решений. Это означает, что когда вы знаете, что концепция является бинарной формулой (которую вы даже можете не знать), вы сможете изучить ее с помощью дерева решений (с достаточным количеством примеров) с нулевой ошибкой.

С другой стороны, если вы хотите изучить примерную концепцию с помощью монотонных союзов, вы не сможете этого сделать, потому что бинарные формулы не являются подмножеством монотонных союзов.

(Под подмножествами я подразумеваю в терминах возможных концепций. А из отношения подмножеств можно сделать заявления о содержании целевого концепта в пространстве гипотез.)

Монотонная конъюнкция - это совокупность конъюнкций, в которых переменные не отменяются. И у вас их больше, когда любое из соединений истинно, выход также истинен. Это подмножество DNF, где вы не можете использовать отрицания.

Некоторые понятия могут быть изучены с помощью монтонных союзов, но вы не можете изучить общие понятия бинарных формул по ним. Это означает, что вы не сможете учиться с нулевой ошибкой, общие бинарные формулы не являются подмножеством монотонных соединений.

Вот хороший PDF из Принстона по основам ML: http://www.cs.princeton.edu/courses/archive/spr06/cos511/scribe_notes/0209.pdf