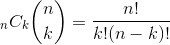Подсчет N вхождений в потолочном диапазоне матрицы за строкой

Question

Я хотел бы подсчитывать каждый раз, когда значение находится в заданном диапазоне в матрице за строкой, а затем суммировать эти логические результаты, чтобы получить "меру согласованности" для каждой строки.

Воспроизводимый пример:

m1 <- matrix(c(1,2,1,6,3,7,4,2,6,8,11,15), ncol=4, byrow = TRUE)


# expected outcome, given a range of +/-1 either side

exp.outcome<-matrix(c(TRUE,TRUE,TRUE,FALSE,
                          TRUE,FALSE,TRUE,TRUE,
                          FALSE,FALSE,FALSE,FALSE), 
                          ncol=4, byrow=TRUE)

Выше я указал ожидаемый результат, в случае, когда каждое значение находится в пределах +/- 1 диапазона любых других значений в этой строке.

В первом ряду m1 первое значение (1) находится в пределах +/- 1 от любого другого значения в этой строке, следовательно, равно TRUE, и так далее.

Напротив, ни одно из значений в строке 4 m1 находятся в пределах одной цифры значения друг друга, и, следовательно, каждому назначается FALSE,

Любые указатели будут высоко оценены?

Обновить:

Благодаря предоставленной помощи я могу теперь подсчитать уникальные пары значений, которые соответствуют критериям потолка для любой произвольно большой матрицы (используя биномиальный коэффициент, k извлекается из n без замены).

Answer 1

Прежде чем перейти к ответу, я просто хотел уточнить, что в своем вопросе вы сказали:

В первом ряду m1 первое значение (1) находится в пределах +/-1 от любого другого значения в этой строке, следовательно, равно TRUE, и так далее.

Тем не мение,

>> m1[1,4]
[1] 6

6 не в пределах +/-1 от 1, и есть FALSE Значение как правильный результат в вашем ответе.

Решение

Это решение должно привести вас к желаемым результатам:

t(apply(
    X = m1,
    # Take each row from the matrix
    MARGIN = 1,
    FUN = function(x) {
        sapply(
            X = x,
            # Now go through each element of that row
            FUN = function(y) {
                # Your conditions
                y %in% c(x - 1) | y %in% c(x + 1)
            }
        )
    }
))

Результаты

      [,1]  [,2]  [,3]  [,4]
[1,]  TRUE  TRUE  TRUE FALSE
[2,]  TRUE FALSE  TRUE  TRUE
[3,] FALSE FALSE FALSE FALSE

Проверьте

Для результатов хранятся как res ,

>> identical(res, exp.outcome)
[1] TRUE

Answer 2

Вот тип аккуратного базового метода R, который использует массив:

Первые две строки - это настройки, которые хранят трехмерный массив допустимых значений и матрицу, которая будет хранить желаемый результат. Структура массива следующая: столбцы соответствуют допустимым значениям матричного элемента в одном столбце. Третье измерение соответствует строкам матрицы.

Предварительное распределение таким образом должно сократить повторные вычисления.

# construct array of all +1/-1 values
valueArray <- sapply(1:nrow(m1), function(i) rbind(m1[i,]-1, m1[i,], m1[i,]+1),
                     simplify="array")

# get logical matrix of correct dimensions
exp.outcome <- matrix(TRUE, nrow(m1), ncol(m1))

# get desired values
for(i in 1:nrow(m1)) {
  exp.outcome[i, ] <- sapply(1:ncol(m1), function(j) m1[i, j] %in% c(valueArray[, -j, i]))
}

Который возвращается

exp.outcome
      [,1]  [,2]  [,3]  [,4]
[1,]  TRUE  TRUE  TRUE FALSE
[2,]  TRUE FALSE  TRUE  TRUE
[3,] FALSE FALSE FALSE FALSE