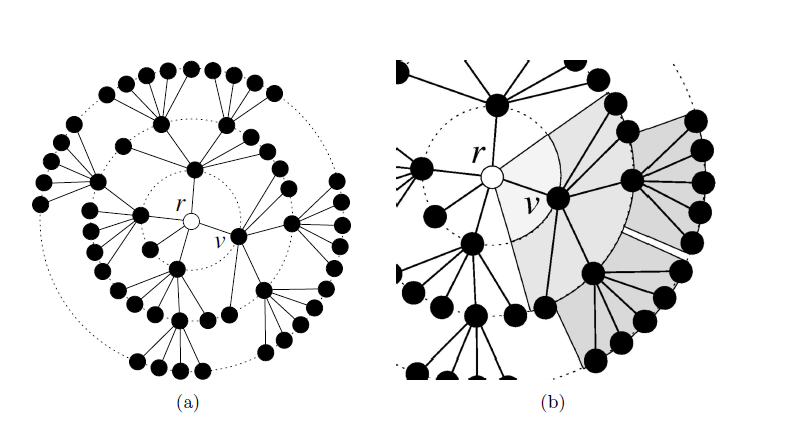
Почему алгоритм рисования макета радиального дерева создает скрещенные ребра?

Question

Я реализую алгоритм рисования радиального макета, согласно публикации г-на Энди Павло, ссылка [страница 18]

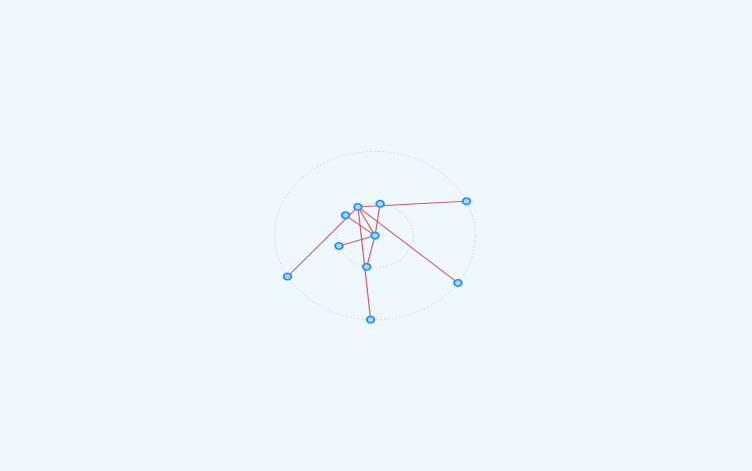
Проблема в том, что мой результат содержит скрещенные ребра. Что является чем-то недопустимым. Я нашел какое-то решение, похожее на проблему, но не смог реализовать их в этом алгоритме (мне пришлось бы изменить весь подход к решению). Кроме того, алгоритм мистера Энди Павло должен быть в состоянии решить эту проблему. Когда мы смотрим на результат его алгоритма, здесь нет скрещенных ребер. Что я делаю неправильно? Я что-то пропустил? Заранее спасибо.

Mr.Pavlo псевдокод алгоритма

Моя реализация алгоритма

        public void RadialPositions(Tree<string> rootedTree, Node<string> vertex, double alfa, double beta,
        List<RadialPoint<string>> outputGraph)
    {
        //check if vertex is root of rootedTree
        if (vertex.IsRoot)
        {
            vertex.Point.X = 0;
            vertex.Point.Y = 0;
            outputGraph.Add(new RadialPoint<string>
            {
                Node = vertex,
                Point = new Point
                {
                    X = 0,
                    Y = 0
                },
                ParentPoint = null
            });

        }
        //Depth of vertex starting from 0
        int depthOfVertex = vertex.Depth;
        double theta = alfa;
        double radius = Constants.CircleRadius + (Constants.Delta * depthOfVertex);

        //Leaves number in the subtree rooted at v
        int leavesNumber = BFS.BreatFirstSearch(vertex);
        foreach (var child in vertex.Children)
        {
            //Leaves number in the subtree rooted at child
            int lambda = BFS.BreatFirstSearch(child);
            double mi = theta + ((double)lambda / leavesNumber * (beta - alfa));

            double x = radius * Math.Cos((theta + mi) / 2.0);
            double y = radius * Math.Sin((theta + mi) / 2.0);

            //setting x and y
            child.Point.X = x;
            child.Point.Y = y;

            outputGraph.Add(new RadialPoint<string>
            {
                Node = child,
                Point = new Point
                {
                    X = x,
                    Y = y,
                    Radius = radius
                },
                ParentPoint = vertex.Point

            });

            if (child.Children.Count > 0)
            {
                child.Point.Y = y;
                child.Point.X = x;
                RadialPositions(rootedTree, child, theta, mi, outputGraph);
            }
            theta = mi;
        }

    }

BFS алгоритм получения листьев

    public static int BreatFirstSearch<T>(Node<T> root)
    {
        var visited = new List<Node<T>>();
        var queue = new Queue<Node<T>>();
        int leaves = 0;

        visited.Add(root);
        queue.Enqueue(root);

        while (queue.Count != 0)
        {
            var current = queue.Dequeue();
            if (current.Children.Count == 0)
                leaves++;
            foreach (var node in current.Children)
            {
                if (!visited.Contains(node))
                {
                    visited.Add(node);
                    queue.Enqueue(node);
                }
            }
        }

        return leaves;
    }

Начальный звонок

        var outputPoints = new List<RadialPoint<string>>();
        alg.RadialPositions(tree, tree.Root,0, 360, outputPoints);

результат mr.Pavlo

Мой результат на простом образце

Answer 1

Math.Cos а также Sin ожидайте, что входной угол будет в радианах, а не в градусах. В вашем первоначальном вызове метода ваш верхний предел угла (beta) должно быть 2 * Math.PIне 360, Это гарантирует, что все углы, которые вы вычисляете, будут в радианах, а не в градусах.