Временная сложность N Queen с помощью возврата?

Question

#include<stdio.h>
#include<math.h>

void printboard(int n);
void fourQueen(int k,int n);
int place(int k,int i);
int x[100];

void NQueen(int k,int n)
{
  int i;
  for(i=1;i<=n;i++)
  {
    if(place(k,i)==1)
    {     x[k]=i;
            if(k==n)
            {
                printf("Solution\n");
                printboard(n);
            }
            else
                NQueen(k+1,n);
    }
  }
}

int place(int k,int i)
{
  int j;
  for(j=1;j<k;j++)
  {
    if((x[j]==i)||abs(x[j]-i)==abs(j-k))
        return 0;
  }
  return 1;
}

void printboard(int n)
{
  int i;
  for(i=1;i<=n;i++)
    printf("%d  ",x[i]);
}

void main()
{
    int n;
    printf("Enter Value of N:");
    scanf("%d",&n);
    NQueen(1,n);
}

Я думаю, что это имеет временную сложность: O(n^n), так как функция NQueen рекурсивно вызывается, но существует ли какая-либо более жесткая граница, возможная для этой программы? как насчет лучшего случая, и наихудшего случая сложности времени. Меня также смущает функция place (), которая называется O(k) и вызывается из NQueen().

Answer 1

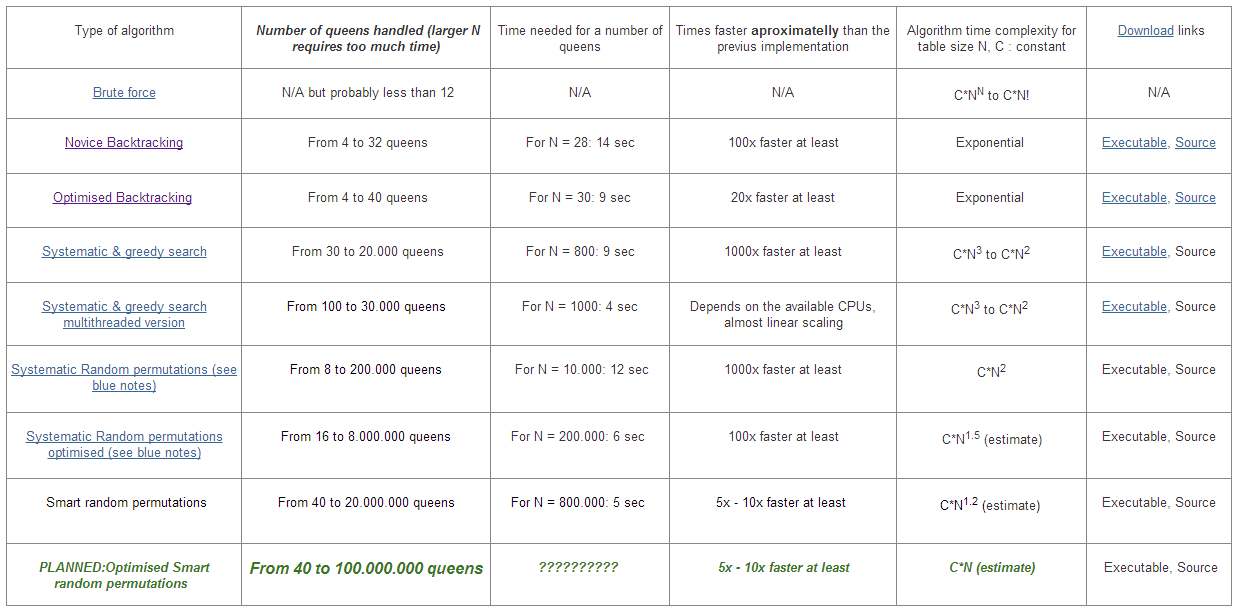
Существует много оптимизаций, которые могут улучшить временную сложность алгоритма.

В этих ссылках есть больше информации:

1. https://sites.google.com/site/nqueensolver/home/algorithm-results

2. https://sites.google.com/site/nqueensolver/home/algorithms/2backtracking-algorithm

Answer 2

Для вашей функции T(n) = n*T(n-1) + O(n^2) что переводится как O(N!) временная сложность в среднем.

Answer 3

ВРЕМЕННАЯ СЛОЖНОСТЬ ПРОБЛЕМЫ N-КОРОЛЕВЫ

> O(N!)

Объяснение: Если мы сложим все это и определим время выполнения как T (N). Тогда T(N) = O(N2) + N*T(N-1). Если вы нарисуете дерево рекурсии, используя это повторение, последний член будет выглядеть примерно так: n3+ n!O(1). По определению Big O, это может быть уменьшено до O(n!) Времени работы.

Answer 4

O(n^n) определенно является верхней границей при решении n-ферзей с использованием возврата. Я предполагаю, что вы решаете это, назначая королеву по столбцам. Однако учтите это: когда вы назначаете местоположение ферзя в первом столбце, у вас есть n опций, после этого у вас есть только n-1 опций, так как вы не можете ферзя в той же строке, что и первая королева, затем н-2 и тд. Таким образом, сложность в худшем случае все еще ограничена сверху O(n!).

Надеюсь, что это отвечает на ваш вопрос, хотя я почти на 4 года опоздал!

Answer 5

Будем считать, что у нас ферзь ладья, то есть нам не нужно заботиться о диагональных конфликтах.

Временная сложность в этом случае будет O(N!)в худшем случае, если бы мы были на охоте, чтобы проверить, существует ли какое-либо решение или нет. Вот простое объяснение.

Возьмем пример, когда N=4.

Предположим, мы хотим заполнить двумерную матрицу. X представляет собой вакантную должность, а 1 представляет собой занятую позицию.

Вначале матрица ответов (которую нам нужно заполнить) выглядит так:

X X X X
X X X X
X X X X
X X X X

Давайте заполним это поле по строкам, то есть выберем одно место в каждой строке, а затем перейдем к следующей строке.

Для первой строки, поскольку в матрице в целом ничего не заполнено, имеем 4 options. Для второй строки имеем3 optionsпоскольку одна строка уже снята. Аналогично для третьей строки имеем2 options и для последней строки у нас остается только 1 option.

Всего вариантов = 4*3*2*1 = 24 (4!)

Так было, если бы у нас ферзь был ладьей, но у нас больше ограничений в случае ферзя. Сложность должна быть меньшеO(N!) по фактическому количеству операций.

Answer 6

Сложность n^n и вот объяснение

Здесь n представляет количество ферзей и останется одинаковым для каждого вызова функции. K - номер строки, и функция будет вызываться до тех пор, пока k не достигнет значения n. Там, если n=8, у нас будет n строк и n ферзей.

T (n) = n (n + t (максимум k - 1))=n^max для k=n^n, так как максимум для k равен n.

Примечание: функция имеет два параметра. В цикле n не уменьшается, для каждого вызова функции оно остается одним и тем же. Но количество вызовов функции уменьшается, так что рекурсия может завершиться.

Answer 7

Сложность (n+1)!n^n начинается с T(i)=O(niT(i+1)), T(n)=n^3. Итак, T(1)=nT(2)=2n^2T(3)=...=(n-1)n^(n-1)!T(n)=(n+1)