MDS-графики двоичных данных: контринтуитивная кластеризация

Question

Скажем, у меня есть следующий двоичный кадр данных, df,

structure(list(a = c(0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0), b = c(0, 
0, 0, 0, 0, 0, 1, 0, 1, 0, 1), c = c(0, 0, 0, 0, 1, 0, 0, 1, 
0, 1, 0), d = c(1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0), e = c(0, 0, 
1, 0, 0, 0, 0, 0, 0, 0, 1), f = c(0, 0, 1, 0, 0, 0, 0, 0, 0, 
0, 1), g = c(0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0), h = c(1, 0, 0, 
0, 0, 0, 0, 1, 1, 0, 0), i = c(0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 
0)), class = "data.frame", row.names = c(NA, -11L), .Names = c("a", 
"b", "c", "d", "e", "f", "g", "h", "i"))

> df
   a b c d e f g h i
1  0 0 0 1 0 0 0 1 0
2  0 0 0 0 0 0 1 0 0
3  0 0 0 0 1 1 1 0 0
4  0 0 0 0 0 0 1 0 0
5  1 0 1 0 0 0 0 0 0
6  0 0 0 0 0 0 0 0 1
7  0 1 0 1 0 0 0 0 0
8  1 0 1 0 0 0 0 1 0
9  0 1 0 0 0 0 0 1 1
10 0 0 1 1 0 0 0 0 1
11 0 1 0 0 1 1 0 0 0

Я хочу изучить сходство между строками и, следовательно, использовать график MDS. Я выполняю классическое масштабирование MDS, используя binary (то есть, Jaccard) метод в dist,

# Load libraries
library(dplyr)
library(ggplot2)
library(magrittr)

# Perform MDS scaling using binary method
mds_df <- df %>% 
  dist(method = "binary") %>% 
  cmdscale 

Затем я помечаю свои столбцы, привязываю их к исходному фрейму данных и добавляю номера строк, которые будут использоваться в качестве меток на моем графике.

# Name columns
colnames(mds_df) <- c("mds_x", "mds_y")

# Bind to original data frame
df %<>% 
  cbind(mds_df) %>% 
  mutate(tags = row_number())

Наконец, я строю свои результаты с ggplot2,

g <- ggplot(df) + geom_point(aes(x = mds_x, y = mds_y), size = 5)
g <- g + geom_text(aes(x = mds_x, y = mds_y, label = tags), position = position_jitter(width = 0.05, height = 0.05))
g <- g + xlab("Coordinate 1") + ylab("Coordinate 2")
print(g)

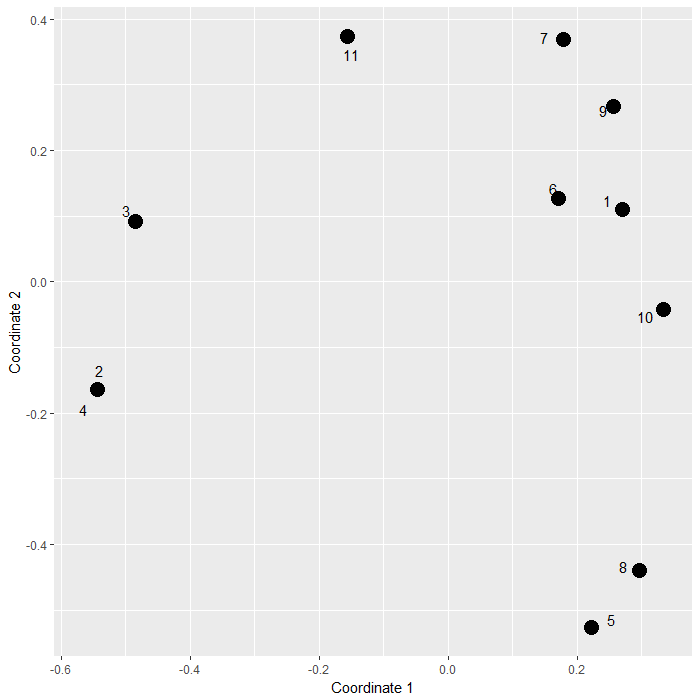
Теперь обратите внимание, что строки 2 и 4 в матрице абсолютно одинаковы. На рисунке они падают прямо друг на друга. Большой! Имеет смысл. Далее посмотрите на строки 6 и 7. Они не имеют общего 1 значения еще падают довольно близко друг к другу. Хм. Что еще хуже, ряды 3 и 11 имеют два 1общие, но расположены гораздо дальше друг от друга. Weird.

Я понимаю, что подход Жакара сравнивает эти общие элементы с общим количеством элементов в обоих наборах (т. Е. Пересекаются через объединение), но строки 6 и 7 имеют три не общих и ни одного общих элемента, тогда как 3 и 11 содержат два элемента в общие и две не общие. Интуитивно я чувствую, что 3 и 11 должны быть ближе друг к другу, чем 6 и 7. Это из-за неправильного выбора метрики расстояния или недостатка в моем коде / логике? Есть ли другой способ построения графиков, который бы показывал эти результаты более интуитивным способом?

Answer 1

Поскольку у вас есть 9 переменных, вы строите 11 наблюдений в 9-мерном пространстве. При сжатии до двухмерного пространства детали теряются. Если вы бежите cmdscale() с eig=TRUE Вы получите больше информации об окончательном решении. GOF ценность - это соответствие формы 1.0. У вас есть.52, поэтому вы отображаете около 52% пространственной информации в 9 измерениях в 2 измерениях. Это хорошо, но не замечательно. Если вы увеличите до 3-х измерений, вы получите GOF значение 0,68. cmdscale() Функция вычисляет метрическое многомерное масштабирование (так называемый анализ главных координат).

Поскольку вы загрузили пакет vegan, у вас есть возможность попробовать неметрическое многомерное (NMDS) масштабирование с monoMDS() или же metaMDS(), Проблема с NMDS состоит в том, что решение может найти локальный минимум, поэтому лучше всего попробовать несколько прогонов и выбрать лучший. Что это metaMDS() делает. По умолчанию он пробует 20 случайных стартовых конфигураций. Если 2 из них по существу идентичны, они сходятся. Ваши данные не находят 2 одинаковых решения, поэтому я просто строю лучшее из 20. trymax=100Я наконец получил конвергентные решения, но это решение не заметно отличается от того, которое использует стандартные 20 попыток:

df.dst <- dist(df, method="binary")
df.meta <- metaMDS(df.dst)
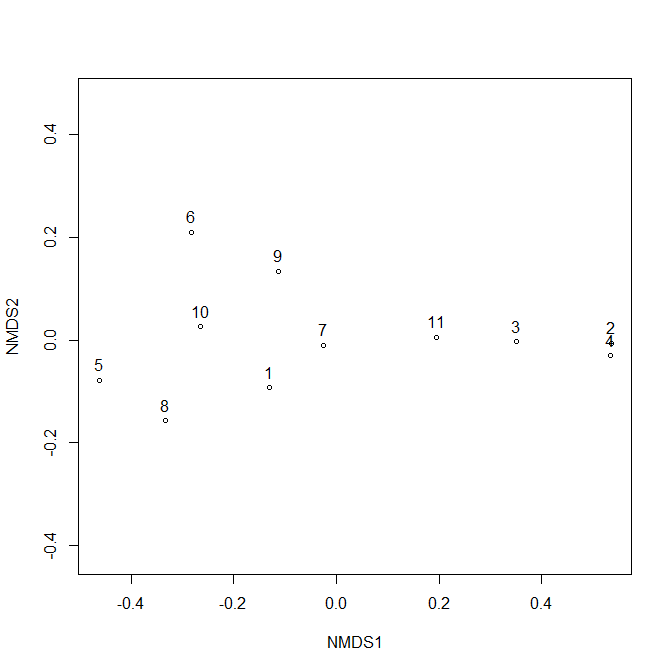
plot(df.meta, "sites")
text(df.meta, "sites", pos=3)

Я думаю, что расстояния немного лучше представлены на этом графике. Конечно, 11 и 3 ближе, чем 6 и 7.