Определить, являются ли два класса линейно разделимыми (алгоритмически в 2D)
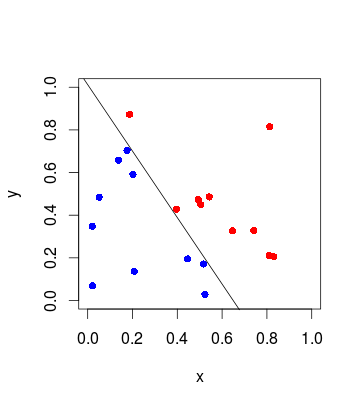
Существует два класса, назовем их X и O. Ряд элементов, принадлежащих этим классам, расположен в плоскости xy. Вот пример, где два класса не являются линейно разделимыми. Невозможно нарисовать прямую линию, которая идеально разделяет X и O на каждой стороне линии.
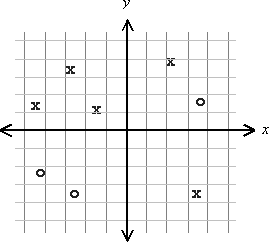
Как вообще определить, являются ли два класса линейно разделимыми?, Меня интересует алгоритм, в котором не делается никаких предположений относительно количества элементов или их распределения. Конечно, алгоритм с наименьшей вычислительной сложностью предпочтителен.
8 ответов
Если вы нашли выпуклый корпус для обоих X точки и O По отдельности (т.е. на этом этапе у вас есть два отдельных выпуклых корпуса), вам нужно будет просто проверить, пересекались ли какие-либо сегменты корпусов и не был ли один корпус закрыт другим.
Если бы было обнаружено, что две оболочки полностью не пересекаются, два набора данных будут геометрически разделены.
Поскольку по определению корпуса являются выпуклыми, любой разделитель будет прямой линией.
Существуют эффективные алгоритмы, которые могут использоваться как для поиска выпуклой оболочки (алгоритм qhull основан на O(nlog(n)) быстрый подход, я думаю), и выполнить тесты пересечения линия-линия для набора сегментов ( линия разметки в O(nlog(n))), поэтому в целом кажется, что эффективный O(nlog(n)) алгоритм должен быть возможным.
Этот тип подхода должен также распространяться на общие k-way разделительные тесты (где у вас есть k групп объектов) путем формирования выпуклой оболочки и проведения испытаний на пересечение для каждой группы.
Он также должен работать в более высоких измерениях, хотя испытания на пересечение станут более сложными...
Надеюсь это поможет.
В вычислительном отношении наиболее эффективный способ определить, являются ли два набора точек линейно разделимыми, - это применение линейного программирования. GLTK идеально подходит для этой цели, и почти каждый язык высокого уровня предлагает интерфейс для него - R, Python, Octave, Julia и т. Д.
Допустим, у вас есть набор точек A и B:
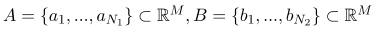
Затем вы должны минимизировать 0 для следующих условий:
(А ниже - это матрица, а не набор точек сверху)
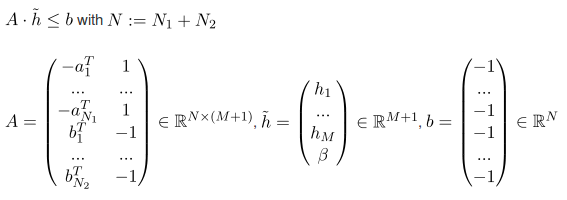
"Минимизация 0" фактически означает, что вам не нужно на самом деле оптимизировать целевую функцию, потому что нет необходимости выяснять, являются ли множества линейно разделимыми.
В конце (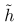
) определяет разделительную плоскость.
Если вас интересует рабочий пример по R или математическим деталям, проверьте это.
Вот наивный алгоритм, который, я уверен, сработает (и, если так, показывает, что проблема не является NP-полной, как утверждает другой пост), но я не удивлюсь, если это можно будет сделать более эффективно: Если разделительная линия существует, ее можно будет перемещать и вращать до тех пор, пока она не достигнет двух из X или одного X и одного O. Поэтому мы можем просто посмотреть на все возможные линии, которые пересекают два X или один X и один O, и посмотрите, являются ли какие-либо из них разделительными линиями. Таким образом, для каждой из пар O(n^2) выполните итерацию по всем n-2 другим элементам, чтобы увидеть, находятся ли все X на одной стороне и все O на другой. Общая сложность времени: O (n ^ 3).
Вычисление линейного SVM с последующим определением, на какой стороне вычисляемой плоскости находятся оптимальные маргинальные точки каждой точки, будет указано, являются ли эти точки линейно разделимыми.
Это излишне, но если вам нужно быстрое одноразовое решение, есть много существующих библиотек SVM, которые сделают это за вас.
Вы, вероятно, можете применить линейное программирование к этой проблеме. Я не уверен в его вычислительной сложности в формальном выражении, но метод успешно применяется для очень больших задач, охватывающих широкий спектр областей.
Линейный персептрон гарантированно найдет такое разделение, если оно существует.
Смотрите: http://en.wikipedia.org/wiki/Perceptron.
Как упоминает ElKamina, линейный персептрон гарантированно найдет решение, если оно существует. Этот подход не эффективен для больших размеров. В вычислительном отношении наиболее эффективный способ определить, являются ли два набора точек линейно разделимыми, - это применение линейного программирования.
Код с примером, чтобы решить, используя Perceptron в Matlab здесь
Что ж, и Perceptron, и SVM (машины опорных векторов) могут сказать, разделимы ли два набора данных линейно, но SVM может найти оптимальную гиперплоскость разделимости. Кроме того, он может работать с n-мерными векторами, а не только с точками.
Он используется в таких приложениях, как распознавание лиц. Рекомендую углубиться в эту тему.
В общем, эта проблема NP-трудна, но есть хорошие приближенные решения, такие как K-средних.