Евклидово расстояние между изображениями
 У меня есть два изображения, скажем
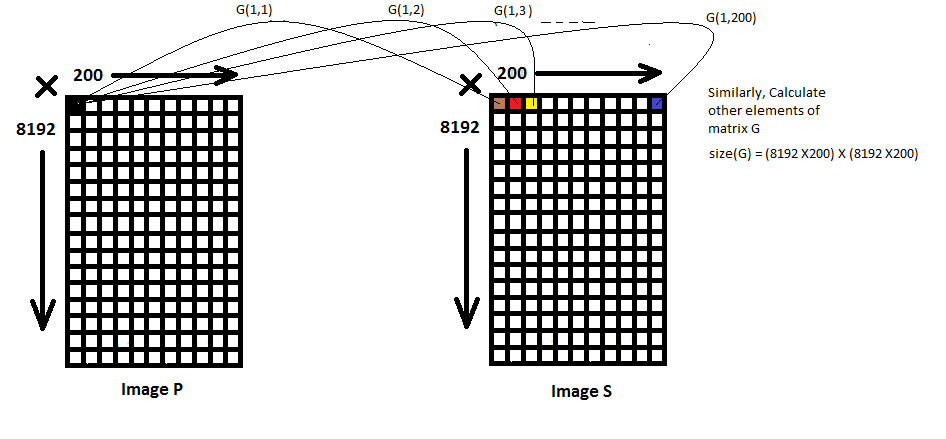
У меня есть два изображения, скажем P а также Sразмером 8192×200, и я хочу вычислить пользовательское "евклидово расстояние" между ними. В настоящее время я использую следующие шаги:
Преобразуйте изображения в пару векторов столбцов и строк:
Ip = Ip(:).'; Is = Is(:);Рассчитать метрическую матрицу,
G, чьи записи задаются по формулеG(i,j) = 1/(2*pi*r*r) * exp((-d*d)/(2*r*r));где
rэто глобальный параметр, который варьируется от 0 до 20, скажем, иdэто расстояние между пикселямиiи пиксельj, Например, если пиксельiявляется(k,l)и пиксельjявляется(k1,l1), затемd = sqrt((k-k1)^2 + (l-l1)^2);, Пиксель 1 будет(1,1)Пиксель 2 будет(1,2), и так далее. Следовательно, размер матрицыGбудет1638400×1638400,Вычислить окончательное (скалярное) евклидово расстояние между двумя изображениями, используя:
ImEuDist = sqrt( (Ip-Is) * G * (Ip-Is).' );
Я уже написал некоторый код с использованием функции mex, но это займет слишком много времени, прежде чем дать результаты (5-6 часов) - см. Этот SO вопрос для кода и дополнительные обсуждения по этому вопросу.
Пожалуйста, помогите мне оптимизировать это; В идеале мне бы хотелось, чтобы он работал в считанные секунды. Обратите внимание, что меня не интересуют решения с участием графического процессора.
1 ответ
Если я правильно понял, вы должны быть в состоянии сделать следующее, и он запустится до 2s:
Пример данных:
s1 = 8192; s2 = 200;
img_a = rand(s1, s2);
img_b = rand(s1, s2);
r = 2;
и сам расчет:
img_diff = img_a - img_b;
kernel = bsxfun(@plus, (-s1:s1).^2.', (-s2:s2).^2);
kernel = 1/(2/pi/r^2) * exp(-kernel/ (2*r*2));
g = conv2(img_diff, kernel, 'same');
res = g(:)' * img_diff(:);
res = sqrt(res);
Выше занимает около 25 с. Чтобы опуститься до 2с, нужно заменить стандартную conv2 с более быстрой сверткой на основе БПФ. Смотрите это и это:
function c = conv2fft(X, Y)
% ignoring small floating-point differences, this is equivalent
% to the inbuilt Matlab conv2(X, Y, 'same')
X1 = [X zeros(size(X,1), size(Y,2)-1);
zeros(size(Y,1)-1, size(X,2)+size(Y,2)-1)];
Y1 = zeros(size(X1));
Y1(1:size(Y,1), 1:size(Y,2)) = Y;
c = ifft2(fft2(X1).*fft2(Y1));
c = c(size(X,1)+1:size(X,1)+size(X,1), size(X,2)+1:size(X,2)+size(X,2));
end
Кстати, если вы все еще хотите, чтобы он шел быстрее, вы могли бы использовать тот факт, что exp(-d^2/r^2) становится очень близко к нулю для довольно маленького d: так что вы можете фактически обрезать свое ядро до крошечного прямоугольника, а не из огромной вещи, предложенной выше. Меньшее ядро означает conv2fft (или особенно conv2) будет работать быстрее.