Получить вершины эллипса на эллиптическом ковариационном графике (создан `car::ellipse`)

Question

Следуя этому посту, можно нарисовать эллипс с заданной матрицей формы (A):

library(car)
A <- matrix(c(20.43, -8.59,-8.59, 24.03), nrow = 2)
ellipse(c(-0.05, 0.09), shape=A, radius=1.44, col="red", lty=2, asp = 1)

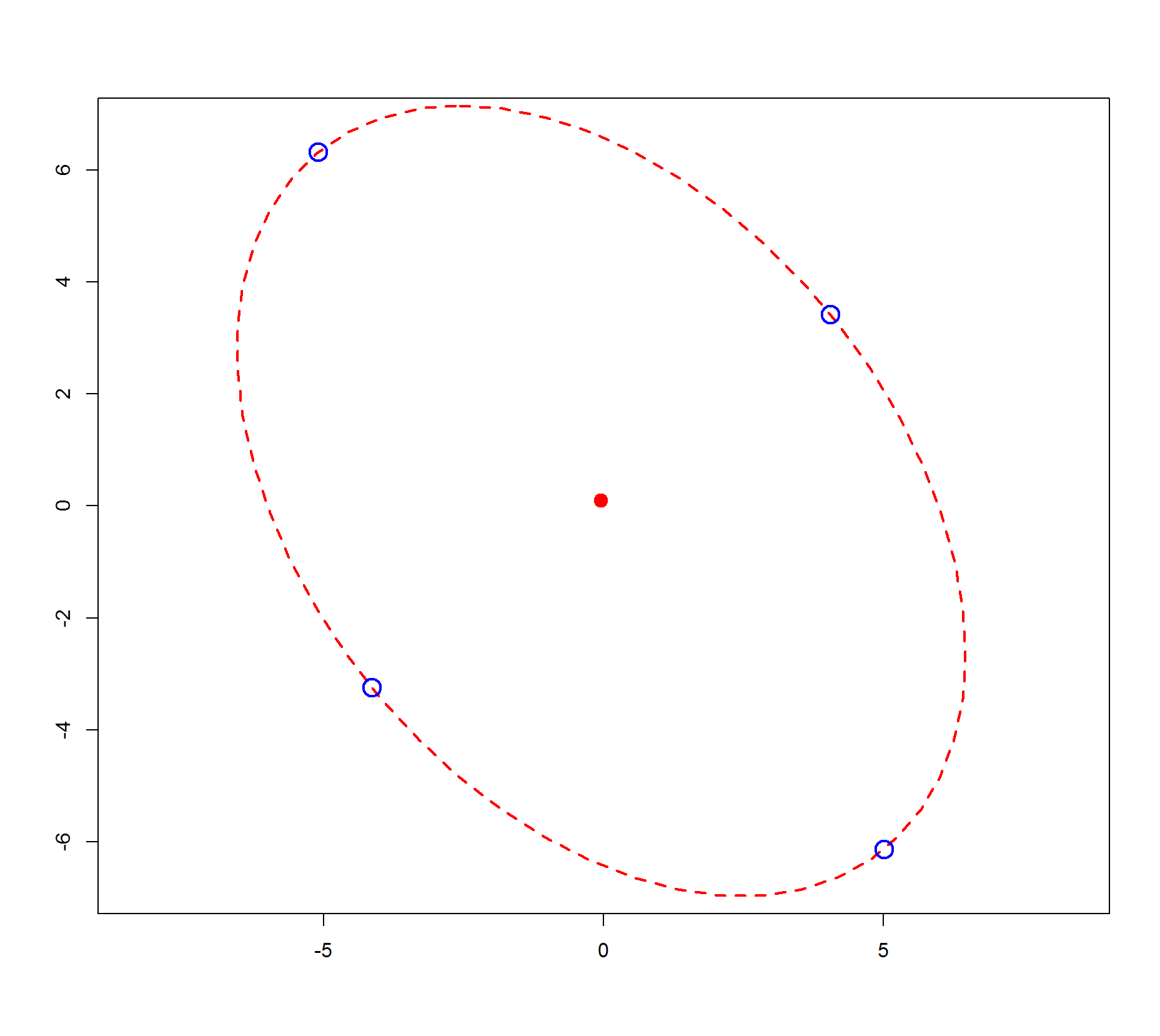
Теперь, как получить главные / второстепенные (пара точек пересечения большой / малой оси и эллипса) вершины этого эллипса?

Answer 1

Для практических целей ответ @Tensibai, вероятно, достаточно хорош. Просто используйте достаточно большое значение для segments аргумент, так что точки дают хорошее приближение к истинным вершинам.

Если вы хотите что-то более строгое, вы можете выбрать местоположение вдоль эллипса, которое максимизирует / минимизирует расстояние от центра, параметризованное углом. Это сложнее, чем просто angle={0, pi/2, pi, 3pi/2} из-за наличия матрицы формы. Но это не так уж сложно

# location along the ellipse
# linear algebra lifted from the code for ellipse()
ellipse.loc <- function(theta, center, shape, radius)
{
    vert <- cbind(cos(theta), sin(theta))
    Q <- chol(shape, pivot=TRUE)
    ord <- order(attr(Q, "pivot"))
    t(center + radius*t(vert %*% Q[, ord]))
}

# distance from this location on the ellipse to the center 
ellipse.rad <- function(theta, center, shape, radius)
{
    loc <- ellipse.loc(theta, center, shape, radius)
    (loc[,1] - center[1])^2 + (loc[,2] - center[2])^2
}

# ellipse parameters
center <- c(-0.05, 0.09)
A <- matrix(c(20.43, -8.59, -8.59, 24.03), nrow=2)
radius <- 1.44

# solve for the maximum distance in one hemisphere (hemi-ellipse?)
t1 <- optimize(ellipse.rad, c(0, pi - 1e-5), center=center, shape=A, radius=radius, maximum=TRUE)$m
l1 <- ellipse.loc(t1, center, A, radius)

# solve for the minimum distance
t2 <- optimize(ellipse.rad, c(0, pi - 1e-5), center=center, shape=A, radius=radius)$m
l2 <- ellipse.loc(t2, center, A, radius)

# other points obtained by symmetry
t3 <- pi + t1
l3 <- ellipse.loc(t3, center, A, radius)

t4 <- pi + t2
l4 <- ellipse.loc(t4, center, A, radius)

# plot everything
MASS::eqscplot(center[1], center[2], xlim=c(-7, 7), ylim=c(-7, 7), xlab="", ylab="")
ellipse(center, A, radius, col="red", lty=2)
points(rbind(l1, l2, l3, l4), cex=2, col="blue", lwd=2)

Answer 2

Я знаю, что этот вопрос был сочтен решенным, но на самом деле есть очень элегантное решение, всего лишь в нескольких строках. Такое вычисление является точным, без какой-либо числовой оптимизации.

## target covariance matrix
A <- matrix(c(20.43, -8.59,-8.59, 24.03), nrow = 2)

E <- eigen(A, symmetric = TRUE)  ## symmetric eigen decomposition
U <- E[[2]]  ## eigen vectors, i.e., rotation matrix
D <- sqrt(E[[1]])  ## root eigen values, i.e., scaling factor

r <- 1.44  ## radius of original circle
Z <- rbind(c(r, 0), c(0, r), c(-r, 0), c(0, -r))  ## original vertices on major / minor axes
Z <- tcrossprod(Z * rep(D, each = 4), U)  ## transformed vertices on major / minor axes

#          [,1]      [,2]
#[1,] -5.055136  6.224212
#[2,] -4.099908 -3.329834
#[3,]  5.055136 -6.224212
#[4,]  4.099908  3.329834

C0 <- c(-0.05, 0.09)  ## new centre
Z <- Z + rep(C0, each = 4)  ## shift to new centre

#          [,1]      [,2]
#[1,] -5.105136  6.314212
#[2,] -4.149908 -3.239834
#[3,]  5.005136 -6.134212
#[4,]  4.049908  3.419834

Чтобы объяснить математику, я собираюсь сделать 3 шага:

1. Откуда этот Эллипс?
2. Метод разложения Холецкого и его недостатки.
3. Метод собственных разложений и его естественная интерпретация.

---

Откуда этот эллипс?

На практике этот эллипс можно получить путем некоторого линейного преобразования в единичный круг x ^ 2 + y ^ 2 = 1,

---

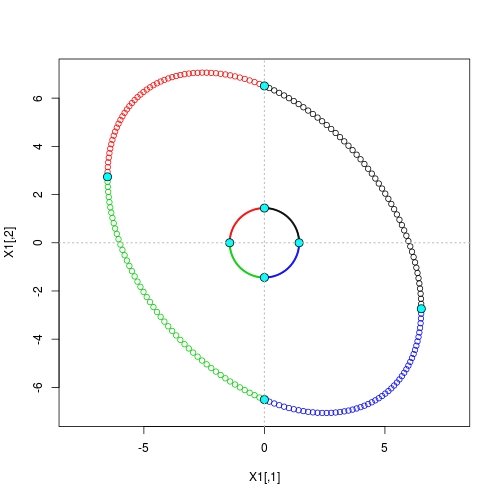
Метод разложения Холецкого и его недостатки

## initial circle
r <- 1.44
theta <- seq(0, 2 * pi, by = 0.01 * pi)
X <- r * cbind(cos(theta), sin(theta))

## target covariance matrix
A <- matrix(c(20.43, -8.59,-8.59, 24.03), nrow = 2)

R <- chol(A)  ## Cholesky decomposition
X1 <- X %*% R  ## linear transformation

Z <- rbind(c(r, 0), c(0, r), c(-r, 0), c(0, -r))  ## original vertices on major / minor axes
Z1 <- Z %*% R  ## transformed coordinates

## different colour per quadrant
g <- floor(4 * (1:nrow(X) - 1) / nrow(X)) + 1

## draw ellipse
plot(X1, asp = 1, col = g)
points(Z1, cex = 1.5, pch = 21, bg = 5)

## draw circle
points(X, col = g, cex = 0.25)
points(Z, cex = 1.5, pch = 21, bg = 5)

## draw axes
abline(h = 0, lty = 3, col = "gray", lwd = 1.5)
abline(v = 0, lty = 3, col = "gray", lwd = 1.5)

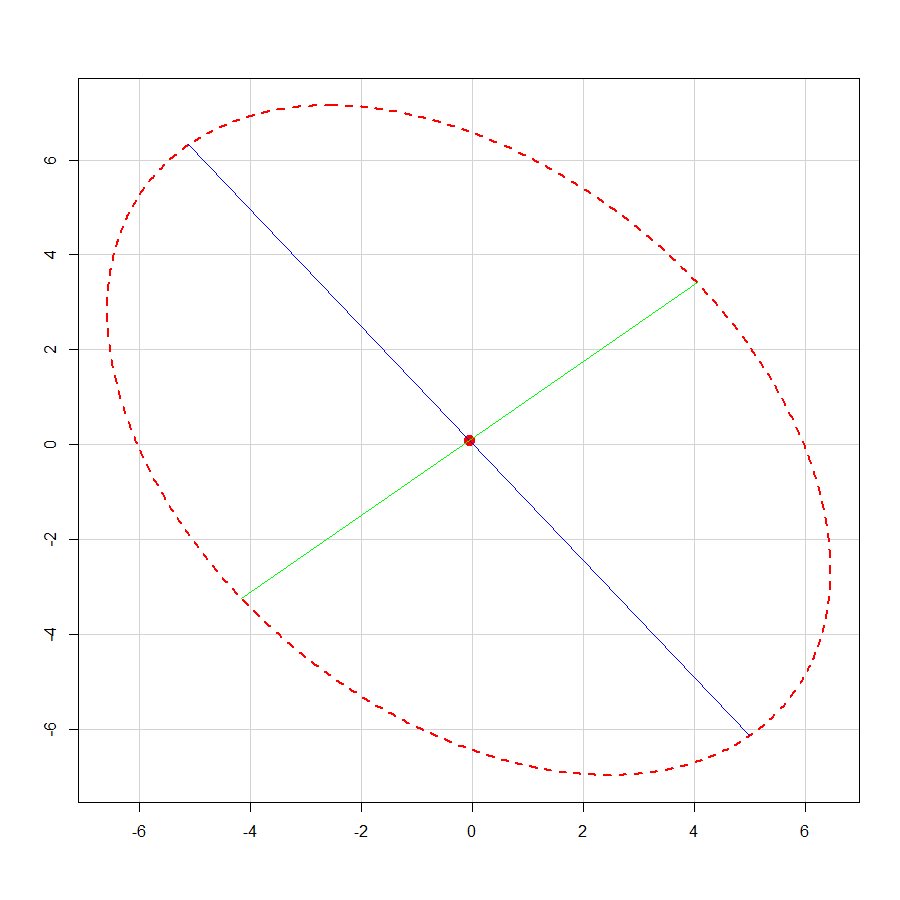
Мы видим, что матрица линейного преобразования R не имеет естественной интерпретации. Исходные вершины круга не отображаются на вершины эллипса.

---

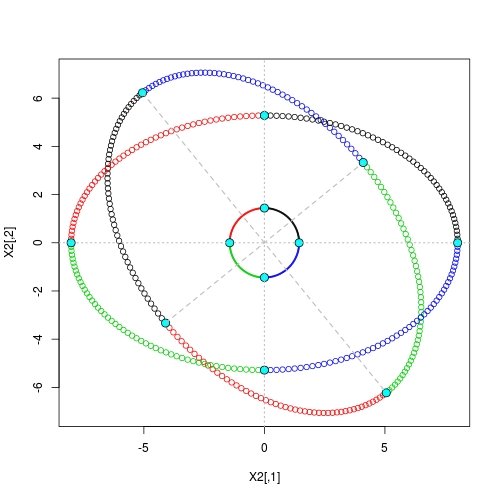
Метод собственных разложений и его естественная интерпретация

## initial circle
r <- 1.44
theta <- seq(0, 2 * pi, by = 0.01 * pi)
X <- r * cbind(cos(theta), sin(theta))

## target covariance matrix
A <- matrix(c(20.43, -8.59,-8.59, 24.03), nrow = 2)

E <- eigen(A, symmetric = TRUE)  ## symmetric eigen decomposition
U <- E[[2]]  ## eigen vectors, i.e., rotation matrix
D <- sqrt(E[[1]])  ## root eigen values, i.e., scaling factor

r <- 1.44  ## radius of original circle
Z <- rbind(c(r, 0), c(0, r), c(-r, 0), c(0, -r))  ## original vertices on major / minor axes

## step 1: re-scaling
X1 <- X * rep(D, each = nrow(X))  ## anisotropic expansion to get an axes-aligned ellipse
Z1 <- Z * rep(D, each = 4L)  ## vertices on axes

## step 2: rotation
Z2 <- tcrossprod(Z1, U)  ## rotated vertices on major / minor axes
X2 <- tcrossprod(X1, U)  ## rotated ellipse

## different colour per quadrant
g <- floor(4 * (1:nrow(X) - 1) / nrow(X)) + 1

## draw rotated ellipse and vertices
plot(X2, asp = 1, col = g)
points(Z2, cex = 1.5, pch = 21, bg = 5)

## draw axes-aligned ellipse and vertices
points(X1, col = g)
points(Z1, cex = 1.5, pch = 21, bg = 5)

## draw original circle
points(X, col = g, cex = 0.25)
points(Z, cex = 1.5, pch = 21, bg = 5)

## draw axes
abline(h = 0, lty = 3, col = "gray", lwd = 1.5)
abline(v = 0, lty = 3, col = "gray", lwd = 1.5)

## draw major / minor axes
segments(Z2[1,1], Z2[1,2], Z2[3,1], Z2[3,2], lty = 2, col = "gray", lwd = 1.5)
segments(Z2[2,1], Z2[2,2], Z2[4,1], Z2[4,2], lty = 2, col = "gray", lwd = 1.5)

Здесь мы видим, что на обоих этапах преобразования вершины по-прежнему отображаются в вершины. Именно на основе такого свойства мы имеем аккуратное решение, данное в самом начале.

Answer 3

Все еще крайне неуверенный, это действительно ответит на вопрос, но вот моя попытка:

Сначала определим центр эллипса как вектор для последующего использования:

center<-c(x=-0.05, y=0.09)

нарисуйте эллипс и получите матрицу "точек" с достаточными значениями, чтобы получить точку, достаточно близкую к точке реальности:

tmp<-ellipse(c(-0.05, 0.09), shape=A, radius=1.44, segments=1e3, col="red", lty=2,add=FALSE)

Создайте из него таблицу данных и вычислите расстояние каждой точки до центра (точка_x - центр_х)² + (точка_у - центр_у)²:

dt <- data.table(tmp)
dt[,dist:={dx=x-center[1];dy=y-center[2];dx*dx+dy*dy}]

Упорядочить вершины по расстоянию:

setorder(dt,dist)

Получите минимальные и максимальные баллы:

> tail(dt,2)
           x         y     dist
1:  4.990415 -6.138039 64.29517
2: -5.110415  6.318039 64.29517
> head(dt,2)
       x        y     dist
1:  4.045722  3.41267 27.89709
2: -4.165722 -3.23267 27.89709

Не добавляйте слишком много сегментов, иначе два первых значения будут двумя точками, расположенными очень близко друг к другу, а не напротив.

с визуальными результатами это звучит не очень точно в конце: