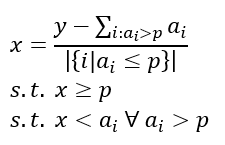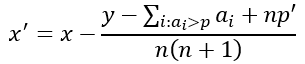Как решить уравнение sum{max(a_i, x)}=y с переменной x? Есть ли алгоритм с O(n) сложностью по времени?

Question

Я пытаюсь найти алгоритм для решения следующего уравнения:

∑ max (a_i, x) = y

в которой a_i являются константами, а x является переменной.

Я могу найти алгоритм с O (n log n) временной сложностью следующим образом:

Прежде всего, отсортируйте a_i за O (n log n) и установите интервалы
(−∞, a₀), (a₀, a₁),…, (a_i, a_i+1),…, (a_{n −1}, a_n), (a_n, ∞)

Затем для каждого интервала предположим, что x принадлежит этому интервалу, и решите уравнение. Мы могли бы получить x̂, а затем проверить, принадлежит ли x̂ этому интервалу или нет. Если x̂ принадлежит соответствующему интервалу, мы присвоим x̂ x и вернем x. С другой стороны, мы попробуем следующий интервал, пока не получим решение.

Вышеуказанный метод является алгоритмом O (n log n) из-за сортировки. С определением задачи решения уравнения я ожидаю алгоритм с O (n) временной сложностью. Есть ли ссылка на эту проблему?

Answer 1

Прежде всего, это имеет решение, только если сумма всех a_i меньше чем y, Сначала вы должны проверить это, потому что алгоритм ниже зависит от этого свойства.

Предположим, что мы выбрали какой-то опорный пункт p из всех a_i и хочу рассчитать x что соответствует интервалу [p, q), где q следующий больше a_i, Это:

Если вы двигаетесь p к следующему большему a_i, x изменяется следующим образом:

, где p' это новый стержень и n это старое число a_i которые меньше или равны p, При условии, что сумма всех a_i меньше чем yэто явно приводит к уменьшению x, Точно так же, если мы выберем меньшее p, x увеличена.

Возвращаясь к первому уравнению, мы можем наблюдать следующее: x меньше чем pмы должны выбрать меньшее p, Если x больше, чем самый маленький из больших a_is, мы должны выбрать больший p, В любом другом случае мы нашли правильное x,

Это может быть использовано в процедуре быстрого выбора. Комментарий @MvG привел меня на этот трек. Все кредиты за идею быстрого выбора идут к нему. Вот некоторый псевдокод (модифицированная версия из Википедии):

findX(list, y)
    left := 0
    right := length(list) - 1
    sumGreater := 0 // the sum of all a_i greater than the current interval
    numSmaller := 0 // the number of all a_i smaller than the current interval
    minGreater := inf //the minimum of all a_i greater than the current interval
    loop
        if left = right
            return (y - sumGreater) / (numSmaller + 1)
         pivotIndex := medianOfMedians(list, left, right)
         //the partition function will also sum the elements larger than the pivot, 
         //count the elements smaller than the pivot, and find the minimum of the
         //larger elements
         (pivotIndex, partialSumGreater, partialNumSmaller, partialMinGreater) 
             := partition(list, left, right, pivotIndex)

         x := (y - sumGreater - partialSumGreater) / (numSmaller + partialNumSmaller + 1)

        if(x >= list[pivotIndex] && x < min(partialMinGreater, minGreater))
            return x
        else if x < list[pivotIndex]
            right := pivotIndex - 1
            minGreater := list[pivotIndex]
            sumGreater += partialSumGreater + list[pivotIndex]
        else
            left := pivotIndex + 1
            numSmaller += partialNumSmaller + 1

Основная идея заключается в том, что функция секционирования собирает некоторую дополнительную статистику. Это не меняет временную сложность функции разделения, потому что это требует O(n) дополнительные операции, оставляя общую сложность времени O(n) для функции разделения. medianOfMedians функция также линейна по времени. Остальные операции в цикле имеют постоянное время. Предполагая, что медиана медиан дает хорошие точки, общее время всего алгоритма составляет примерно O(n + n/2 + n/4 + n/8 ...) = O(n),

Answer 2

Поскольку комментарии могут быть удалены, я превращаю свои собственные комментарии в последовательный ответ. Вопреки первоначальному вопросу, я использую индексы с 1 по n, избегая первоначально использованного а ₀. Так что это последовательная индексация на основе одного индекса с использованием инклюзивных индексов.

Предположим на данный момент, что b _i - это коэффициенты от вашего ввода, но в отсортированном порядке, поэтому b _i ≤ b _{i +1}. Как вы, по сути, уже писали, если b _i ≤ x≤ b _{i +1,} то результатом будет i ⋅ x + b _{i +1} + ⋯ + b _n, поскольку первые члены i будут использовать x, а другие члены будут использовать b _Дж. Решая для x, вы получаете x = (y - b _{i +1} - ⋯ - b _n) / i и помещая это обратно в свое неравенство, вы получаете i ⋅ b _i ≤ y - b _{i +1} - ⋯ - b _n ≤ i ⋅ б _{я +1}. Концентрируясь на одном из неравенств, вы хотите наибольшее, такое, что

i ⋅ b _i ≤ y - b _{i +1} - ⋯ - b _n (впоследствии называемое "неравенством")

Но чтобы сделать эту работу на несортированном _i, вам нужно что-то похожее на медиану медиан. Это алгоритм, который обеспечивает гарантированное поведение O (n) в худшем случае для задачи выбора медианы, где типичный быстрый выбор будет принимать O (n ²) в худшем случае, хотя на практике это обычно довольно хорошо.

На самом деле ваша проблема ничем не отличается от быстрого выбора. Вы можете выбрать коэффициент поворота и разделить остаток на большие и меньшие значения. Затем вы оцениваете неравенство для основного элемента. Если оно выполнено, вы вернетесь в список более крупных элементов, в противном случае вы вернетесь в список более мелких элементов, пока в какой-то момент у вас не появится два смежных элемента, один из которых удовлетворяет неравенству, а другой - нет.

В худшем случае это O (n ²), поскольку вам может потребоваться O (n) рекурсивных вызовов, каждый из которых тратит O (n) время на обработку своего ввода. Как и сам быстрый выбор O (n ²), он неоптимален. Медиана медиан показывает, что эта проблема действительно может быть решена с помощью O (n). Поэтому нам нужно либо найти подобное решение здесь, либо переформулировать эту проблему здесь с точки зрения нахождения медианы, либо написать некоторый алгоритм, который разумно использует медиану.

На самом деле Nico Schertler нашел способ реализовать этот последний вариант: возьмите алгоритм, который я описал выше, но выберите медианный элемент pivot. Таким образом, вы можете гарантировать, что каждый рекурсивный вызов будет обрабатывать в два раза меньше информации, чем предыдущий. Поскольку медиана медиан сама по себе равна O (n), это можно сделать без превышения границы O (n) для каждого рекурсивного вызова.

Таким образом, в псевдокоде это выглядит так (используя инклюзивные индексы):

# f: Process whole problem with coefficients a_1 through a_n
f(y, a, n) := begin
  if y < (sum of a_i for i from 1 through n):                             #  O(n)
    throw Error "Cannot satisfy equation"  # Or omit check and risk division by zero 
  return g(a, 1, n, y)                                                    #  O(n)
end

# g: Recursively process part of the problem, namely a_l through a_r
# Precondition: we know inequality holds for i = l - 1 and fails for i = r + 1
# a: the array as provided to f; will get modified in place
# l: left index (inclusive)
# r: right index (inclusive)
# y: (original y) - (sum of a_j for j from r + 1 through n)
g(a, l, r, y) := begin              # process a_l through a_r                O(r-l)
  if r < l:                         # inequality holds in r but fails in l   O(1)
    return y / r                    # compute x for the case of i = r        O(1)
  m = median(a, l, r)               # computed using median of medians       O(r-l)
  i = floor((l + r) / 2)            # index of median, with same tie breaks  O(1)
  partition(a, l, r, m)             # so a_l…a_(i-1) ≤ a_i=m ≤ a_(i+1)…a_r   O(r-l)
  rhs = y - (sum of a_j for j from i + 1 to r)                            #  O((r-l)/2)
  if i * a_i ≤ rhs:                 # condition holds, check larger i
    return g(a, i + 1, r, y)        # recurse in right half of list          O((r-l)/2)
  else:                             # condition fails, check smaller i
    return g(a, l, i - 1, rhs - m)  # recurse in left half of list           O((r-l)/2)
end