Практические применения интервального дерева

Question

Я немного погуглил на эту тему и нашел это на http://www.geeksforgeeks.org/

Дерево интервалов в основном представляет собой геометрическую структуру данных и часто используется для создания оконных запросов, например, для поиска всех дорог на компьютеризированной карте внутри прямоугольного видового экрана или для поиска всех видимых элементов в трехмерной сцене.

Теперь мой вопрос состоит из двух частей:

• Как интервальное дерево используется для поиска всех дорог на компьютерной карте?
• Какие еще примеры практического применения интервального дерева?

PS: краткие пояснения со ссылкой на больше материалов для чтения по дереву интервалов будут более чем приветствоваться

Answer 1

В запросе окон, учитывая набор отрезков и прямоугольник, выровненный по оси, мы должны найти пересечения отрезков с прямоугольником. Эту проблему можно решить, используя деревья интервалов в сочетании с деревьями дальности.

Деревья диапазонов - это эффективная структура данных для нахождения набора точек, находящихся в пределах диапазона / прямоугольника. Таким образом, они могут быть использованы для поиска всех отрезков линии, так что одна из конечных точек каждого отрезка линии присутствует в прямоугольнике запроса. Они соответствуют отрезкам синей линии на рисунке ниже.

Деревья интервалов можно использовать для поиска тех сегментов, которые перекрываются с окном, но чьи конечные точки находятся за пределами окна. Это красные сегменты на рисунке.

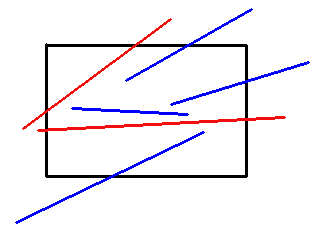
Прежде чем решить эту проблему, представьте себе более ограниченную версию проблемы, в которой все отрезки линии горизонтальны или вертикальны. В этом случае любой горизонтальный сегмент, который пересекает прямоугольник, должен пересекать левый (и правый) вертикальный край прямоугольника. Если мы рассматриваем горизонтальные сегменты как интервалы, а вертикальный край прямоугольника как точку, проблема состоит в том, чтобы найти все интервалы, которые содержат точку. Таким образом, мы можем решить эту проблему, используя интервальные деревья. Точно так же мы можем найти все пересекающиеся вертикальные отрезки.

Общий вариант проблемы, когда отрезки не параллельны оси, не может быть полностью решен с помощью интервальных деревьев. Однако мы можем использовать деревья интервалов, чтобы исключить подавляющее большинство отрезков, которые не пересекаются с прямоугольником запроса. Для каждого отрезка линии на входе мы строим прямоугольный с осью прямоугольник, диагональ которого - отрезок линии. Затем мы строим (горизонтальные и вертикальные) интервальные деревья, используя стороны прямоугольников. Для заданного прямоугольника запроса R мы можем сначала найти все прямоугольники, которые пересекают R, как и раньше. Соответствующие отрезки имеют высокую вероятность пересечения с R и могут быть проверены отдельно для фактического пересечения.

Answer 2

Возможно, не отвечу напрямую на ваш вопрос, но я думаю, что это может помочь

Включающая проблему поиска по интервалам: Учитывая набор S из n интервалов и точку запроса q, сообщите все эти интервалы, содержащие q.

Проблема с поиском перекрывающихся интервалов: Учитывая набор S из n интервалов и интервал запроса Q, сообщите обо всех этих интервалах в перекрывающемся S Q.

Ссылка (также сравните с другой подобной структурой данных, такой как дерево сегментов): http://www.iis.sinica.edu.tw/~dtlee/dtlee/CRCbook_chapter18.pdf