Разрезать торт или разложить многоугольник
Я сталкиваюсь со следующей проблемой: мне дан набор координат на целочисленной сетке, которые определяют вершины многоугольника. Полигон гарантированно будет выпуклым. Доказано, что такой многоугольник всегда можно разрезать на 4 равные части по 2 ортогональным линиям. Давайте назовем точку пересечения этих линий P, Учитывая этот набор, я должен рассчитать координаты P в пределах многоугольника и под углом необходимо включить линии, чтобы линии разрезали многоугольник на 4 равные части.
Я понимаю, что, вообще говоря, проблема резки тортов не имеет "хорошего" решения. Но этот частный случай этого должен. Я искал алгоритм для решения этой проблемы, но не нашел ничего полезного. Куда мне смотреть?
Мой подход заключается в том, чтобы вычислить координаты центра многоугольника (это можно сделать более или менее легко), разместить Pтут же "покачивайте" линии, пока области частей не совпадут. Но это звучит слишком не элегантно.
UPD: это проблема, с которой я сталкиваюсь. Возможно, этот вопрос следует отложить до тех пор, пока я не приду к актуальным вопросам кода.
1 ответ
Вот частичный эскиз решения:
Выберите произвольное направление и найдите линию, параллельную этому направлению, которая разбивает многоугольник на две части. Чтобы добиться этого, нарисуйте линию каждой вершиной, чтобы разложить многоугольник на плиты. Соответствующие области плит скажут вам, какая плита пересекает желаемую линию. Простая линейная интерполяция даст точное местоположение линии.
Теперь ваш многоугольник разделен на два выпуклых многоугольника. Для каждой половины повторите вышеописанную процедуру, используя перпендикулярное направление. В общем, вы получите два разных сплиттера, и остается только найти направление, в котором они совпадают.
В заданном направлении разделители пересекают четыре конкретных ребра многоугольника. Если вы слегка поверните, они все еще пересекают те же четыре края. Вы можете разложить полный оборот по угловым диапазонам так, чтобы четыре пересекающихся ребра остались прежними.
Зная четыре пересекающихся ребра, вы можете установить отношение, которое сообщает вам расстояние между двумя перпендикулярными разделителями как функцию угла. Затем вы можете вычислить угол, под которым два разделителя совпадают, и проверить, принадлежит ли этот угол диапазону, определенному для этих ребер.
Попробовав все диапазоны по очереди, вы найдете решение.
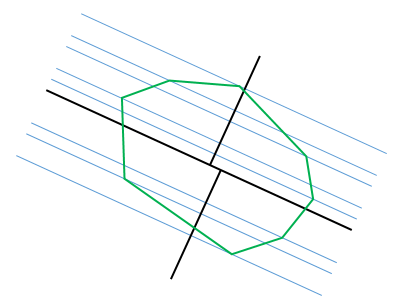
Примечание: пределы угловых диапазонов соответствуют направлениям, параллельным или перпендикулярным линиям, соединяющим две вершины.