CUDA библиотека для вычисления продукта Kronecker

Question

У меня есть приложение, которое требует, чтобы я вычислил несколько больших произведений Кронекера двумерных матриц и умножил результат на большие двумерные матрицы. Я хотел бы реализовать это на графическом процессоре в CUDA и предпочел бы использовать для этого настроенную реализацию библиотеки, а не писать свой собственный (безусловно, неоптимальный) продукт Kronecker. У меня есть опыт работы с CUDA, BLAS, LAPACK и т. Д., Но, к сожалению, в обычных реализациях графического процессора нет функции kron(A,B) (magma, cuBLAS, cula и т. Д.).

Я искал некоторые решения, но не могу найти библиотеку, которая соответствует моим потребностям. (Ближайший вопрос о SO - это параллельный тензорный продукт Kronecker на gpu с использованием CUDA, но это похоже на специальное решение для особого случая, которое не будет соответствовать моим потребностям. Я ищу продукт Kronecker, который будет работать в наиболее общем дело.)

Я читал, что DGEMM в BLAS может быть использован для реализации продукта Kronecker. Существует ли стандартный алгоритм для реализации продукта Kronecker с использованием DGEMM (или его отдельных / сложных вариантов)? Мне кажется, что единственным способом было бы вызвать DGEMM в цикле и объединить результаты в более крупную матрицу, что не очень эффективно. Или кто-нибудь знает другую реализацию или документ, который может предоставить то, что я ищу?

Answer 1

В статье, на которую вы ссылаетесь, используется следующая личность

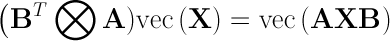
избавить от необходимости явного вычисления продукта Kronecker и замены его вызовом гема 3-го уровня BLAS. Если ваша задача - матричное уравнение, вы можете использовать gemm таким способом, иначе он не будет вам полезен.

Другая идентичность, которая потенциально может быть полезной, - это вычисление продукта Кронекера с использованием внешнего продукта (обновление ранга 1 на уровне 2 BLAS IIRC):

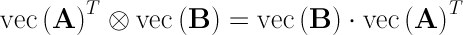
Еще раз отметим, что порядок результирующей матрицы не будет таким же, как произведение Кронекера матриц A и B.

Мне не известна библиотека CUDA для вычисления истинного произведения Кронекера из пары матриц произвольного размера. Это должно быть проблемой, связанной с памятью, поэтому даже относительно наивный подход, который объединяет нагрузки и повторно использует как можно больше данных, должен быть достаточно близок к пиковой пропускной способности.