Вращение 2-мерного массива с использованием NumPy без эффектов наложения

Question

Я хотел бы повернуть только положительные значения пикселей в моем 2d-массиве на несколько градусов относительно центральной точки. Данные представляют концентрации аэрозоля из модели дисперсии шлейфа, а положение дымохода является источником вращения.

Я хотел бы повернуть этот образец рассеивания, учитывая направление ветра.

Концентрации сначала рассчитываются для направления ветра вдоль оси x, а затем переводятся в их повернутое положение, используя двухмерное линейное вращение вокруг центральной точки моего массива (положение дымохода) для всех точек, концентрация которых> 0. Вход X,Y к формуле вращения - это пиксельные индексы.

Моя проблема в том, что выходные данные являются псевдонимами, так как целые числа становятся числами с плавающей точкой. Чтобы получить целые числа, я округлял в большую или меньшую сторону результат. Однако это создает нулевые ячейки, которые становятся все более многочисленными с увеличением угла.

Может ли кто-нибудь помочь мне найти решение моей проблемы? Я хотел бы решить эту проблему, если это возможно, используя numpy или минимум пакетов...

Часть моего сценария, которая касается вычисления концентраций и поворота пикселя на 50° с.ш., следующая. Спасибо за помощь.

def linear2D_rotation(xcoord,ycoord,azimuth_degrees):
    radians = (90 - azimuth_degrees) * (np.pi / 180) # in radians
    xcoord_rotated = (xcoord * np.cos(radians)) - (ycoord * np.sin(radians))
    ycoord_rotated = (xcoord * np.sin(radians)) + (ycoord * np.cos(radians))
    return xcoord_rotated,ycoord_rotated

u_orient = 50 # wind orientation in degres from North
kernel = np.zeros((NpixelY, NpixelX))  # initialize matrix
Yc = int((NpixelY - 1) / 2)  # position of central pixel
Xc = int((NpixelX - 1) / 2)  # position of central pixel

nk = 0
for Y in list(range(0,NpixelX)):
    for X in list(range(0,NpixelY)):
        # compute concentrations only in positive x-direction
        if (X-Xc)>0:
            # nnumber of pixels to origin point (chimney)
            dx = ((X-Xc)+1)
        dy = ((Y-Yc)+1)
        # distance of point to origin (chimney)
        DX = dx*pixel_size_X
        DY = dy*pixel_size_Y
        # compute diffusivity coefficients
        Sy, Sz = calcul_diffusivity_coeff(DX, stability_class)
        # concentration at ground level below the centerline of the plume
        C = (Q / (2 * np.pi * u * Sy * Sz)) * \
            np.exp(-(DY / (2 * Sy)) ** 2) * \
            (np.exp(-((Z - H) / (2 * Sz)) ** 2) + np.exp(-((Z + H) / (2 * Sz)) ** 2))  # at point away from center line
        C = C * 1e9  # convert MBq to Bq

        # rotate only if concentration value at pixel is positive
        if C > 1e-12:
            X_rot, Y_rot = linear2D_rotation(xcoord=dx, ycoord=dy,azimuth_degrees=u_orient)
            X2 = int(round(Xc+X_rot))
            Y2 = int(round(Yc-Y_rot)) # Y increases downwards
            # pixels that fall out of bounds -> ignore
            if (X2 > (NpixelX - 1)) or (X2 < 0) or (Y2 > (NpixelY - 1)):
                continue
            else:
                # replace new pixel position in kernel array
                kernel[Y2, X2] = C

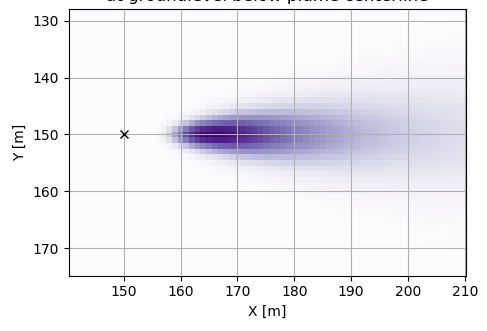
Исходный массив для поворота

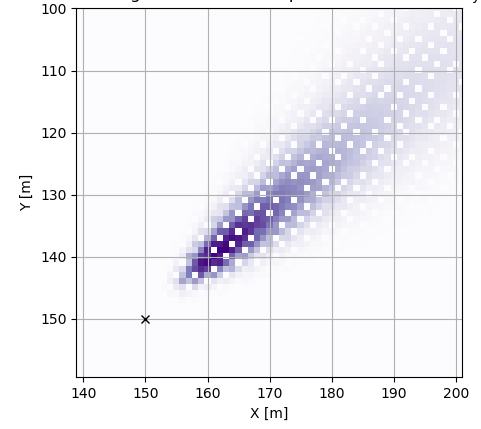
Вращенный массив на 40° с.ш., показывающий потерю данных

Answer 1

Ваше описание проблемы не совсем понятно, но вот несколько рекомендаций:

1.) Не изобретай велосипед. Существуют стандартные решения для таких вещей, как вращение пикселей. Используй их! В этом случае

• scipy.ndimage.affine_transform для выполнения вращения
• однородная координатная матрица для задания поворота
• интерполяция ближайшего соседа (параметр order=0 в коде ниже).

2.) Не зацикливайтесь там, где это не нужно. Скорость, которую вы приобретаете, не обрабатывая неположительные пиксели, ничем не отличается от скорости, которую вы теряете в цикле. Скомпилированные функции могут перебирать множество избыточных нулей, прежде чем рукописный код Python догоняет их.

3.) Не ожидайте решения, которое отображает пиксели один в один, потому что это факт, что будут точки, которые не являются ближайшими соседями, и точки, которые являются ближайшими соседями, к множеству других точек. Имея это в виду, вы можете рассмотреть более гладкую интерполяцию более высокого порядка.

Сравнивая ваше решение со стандартным решением для инструментов, мы обнаруживаем, что последнее

дает сопоставимый результат гораздо быстрее и без этих дырочных артефактов.

Код (без прорисовки). Обратите внимание, что мне пришлось перенести и flipud чтобы выровнять результаты:

import numpy as np
from scipy import ndimage as sim
from scipy import stats

def mock_data(n, Theta=50, put_neg=True):
    y, x = np.ogrid[-20:20:1j*n, -9:3:1j*n, ]
    raster = stats.norm.pdf(y)*stats.norm.pdf(x)
    if put_neg:
        y, x = np.ogrid[-5:5:1j*n, -3:9:1j*n, ]
        raster -= stats.norm.pdf(y)*stats.norm.pdf(x)
        raster -= (stats.norm.pdf(y)*stats.norm.pdf(x)).T
    return {'C': raster * 1e-9, 'Theta': Theta}

def rotmat(Theta, offset=None):
    theta = np.radians(Theta)
    c, s = np.cos(theta), np.sin(theta)
    if offset is None:
        return np.array([[c, -s] [s, c]])
    R = np.array([[c, -s, 0], [s, c,0], [0,0,1]])
    to, fro = np.identity(3), np.identity(3)
    offset = np.asanyarray(offset)
    to[:2, 2] = offset
    fro[:2, 2] = -offset
    return to @ R @ fro

def f_pp(C, Theta):
    m, n = C.shape
    clipped = np.maximum(0, 1e9 * data['C'])
    clipped[:, :n//2] = 0
    M = rotmat(Theta, ((m-1)/2, (n-1)/2))
    return sim.affine_transform(clipped, M, order = 0)

def linear2D_rotation(xcoord,ycoord,azimuth_degrees):
    radians = (90 - azimuth_degrees) * (np.pi / 180) # in radians
    xcoord_rotated = (xcoord * np.cos(radians)) - (ycoord * np.sin(radians))
    ycoord_rotated = (xcoord * np.sin(radians)) + (ycoord * np.cos(radians))
    return xcoord_rotated,ycoord_rotated

def f_OP(C, Theta):
    kernel = np.zeros_like(C)
    m, n = C.shape
    for Y in range(m):
        for X in range(n):
            if X > n//2:
                c = C[Y, X] * 1e9
                if c > 1e-12:
                    dx = X - n//2 + 1
                    dy = Y - m//2 + 1
                    X_rot, Y_rot = linear2D_rotation(xcoord=dx, ycoord=dy,azimuth_degrees=Theta)
                    X2 = int(round(n//2+X_rot))
                    Y2 = int(round(m//2-Y_rot)) # Y increases downwards
                    # pixels that fall out of bounds -> ignore
                    if (X2 > (n - 1)) or (X2 < 0) or (Y2 > (m - 1)):
                        continue
                    else:
                        # replace new pixel position in kernel array
                        kernel[Y2, X2] = c
    return kernel

n = 100
data = mock_data(n, 70)