Разработка программы Secant Method для поиска корней

Question

Поэтому я пытался разработать программу секущих методов, которую можно использовать для поиска корня

f(x) = tanh(x) - (x / 3)

Однако вывод ответа нигде не близко. Каждое найденное мной решение кажется более сложным способом его решения.

    x = 2;
prevx = x;

for i = 1:20

    x = x - (tanh(x)-(x/3))*((x-(prevx))/((tanh(x)-(x/3))-(tanh(prevx))-((prevx/3))));
    prevx = prevx + x;
    x
end

Ответ должен быть 2.987. Я получаю отрицательное число, хотя по какой-то причине.

Answer 1

Вы предполагаете добавить термины, поэтому замените минус в этой строке:

x = x - (tanh(x)-(x/3))*((x-(prevx))/((tanh(x)-(x/3))-(tanh(prevx))-((prevx/3))));

К плюсу:

x = x + (tanh(x)-(x/3))*((x-(prevx))/((tanh(x)-(x/3))-(tanh(prevx))-((prevx/3))));

Чтобы получить желаемый результат 2,987 за х. Также удалите х до конца цикла.

Answer 2

Вот альтернативный способ сделать это (@madbitloman прямо на месте, что касается ошибки в вашем коде).

Секущий метод можно проиллюстрировать следующим образом (из Википедии):

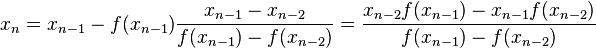
Теперь, если мы переведем это в код MATLAB, это будет выглядеть так:

x(k) = x(k-1) - (f(x(k-1)))*((x(k-1) - x(k-2))/(f(x(k-1)) - f(x(k-2))));

Осталось предоставить алгоритму 2 начальные оценки и некоторое значение допуска, чтобы сообщить ему, когда нужно прекратить поиск корня, то есть когда 2 последовательных записи в x очень близки друг к другу.

Давайте выберем 2 и 4. Чем ближе оценки к реальному корню, тем быстрее сходимость.

Чтобы избежать использования tanh(x)-(x/3) внутри цикла for, который может запутаться, давайте определим анонимную функцию, которая принимает x в качестве аргумента:

f = @(x) tanh(x)-(x/3);

Так что это будет f в строке кода выше.

Следовательно, весь код будет выглядеть следующим образом с допустимым отклонением, скажем, 0,001:

clear
clc

%// Initial values and tolerance
x(1) = 2;
x(2) = 4;
f = @(x) tanh(x)-(x/3);

tolerance = 0.001;

%// Let's try from 3 to 15. 
for k=3:15

    x(k) = x(k-1) - (f(x(k-1)))*((x(k-1) - x(k-2))/(f(x(k-1)) - f(x(k-2))));

    if abs(x(k)-x(k-1)) < tolerance
        break
    end
end

После запуска кода х выглядит так:

x =

    2.0000    4.0000    2.9420    2.9839    2.9847

поэтому потребовалось 5 итераций, чтобы достичь желаемого допуска. Обратите внимание, что из-за плавающей арифметики вы можете использовать меньший допуск, потому что Matlab хранит числа с гораздо большим количеством цифр, чем 4.

Наконец, вы также можете получить отрицательный корень, используя соответствующие начальные оценки, такие как -2 и -4:

x =

   -2.0000   -4.0000   -2.9420   -2.9839   -2.9847

Надеюсь, это поможет как-то!