Применение той же функции к каждому элементу в массиве в C

Question

Скажем, мне нужно найти евклидово расстояние от одной (x,y) координаты до каждой координаты в массиве миллионов координат, а затем выбрать координату с наименьшим расстоянием.

В настоящее время я зацикливаюсь на массиве из миллиона элементов, рассчитываю расстояние, отслеживая минимум. Есть ли способ, которым я мог бы сделать это по-другому и быстрее.

Спасибо

Answer 1

Вы можете значительно улучшить свой алгоритм, используя более сложную структуру данных, например дерево kd. Тем не менее, если вы ожидаете просто один раз найти ближайшего соседа, вы не сможете выполнить лучше, чем перебирать все точки.

Что вы можете сделать, хотя оптимизировать функцию, которая вычисляет расстояние, а также (как уже упоминалось в комментариях) вы можете опустить квадратный корень, поскольку сравнение квадратов двух неотрицательных целых чисел точно так же, как сравнение значений.

Answer 2

Что я понимаю из вопроса, так это то, что вы хотите найти ближайшую пару точек. Для решения этой проблемы существует алгоритм " Ближайшая пара точек".

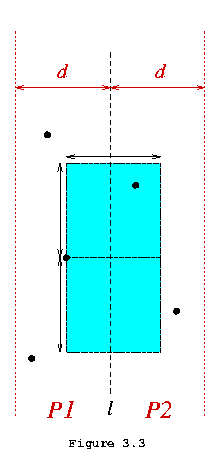
Ближайшая пара из набора точек:

• Разделите набор на две равные части по линииlи рекурсивно вычислить минимальное расстояние в каждой части.
• Позволятьdбыть минимальным из двух минимальных расстояний.
• Устранить точки, которые лежат дальше, чем г, кромеl
• Сортировка оставшихся точек по их y-координатам
• Просканируйте оставшиеся точки в порядке y и вычислите расстояния каждой точки до ее пяти соседей.
• Если любое из этих расстояний меньше d затем обновитеd,

Весь алгоритм ближайшей пары занимаетO(logn*nlogn)знак равноO(nlog2n) время.

Мы можем немного улучшить этот алгоритм, сократив время, необходимое для сортировки по координате y на шаге 4. Это делается с помощью запроса, чтобы рекурсивное решение, вычисленное на шаге 1, возвращало точки в отсортированном порядке по их координатам y. Это даст два отсортированных списка точек, которые нужно только объединить (операция с линейным временем) на шаге 4, чтобы получить полный отсортированный список. Следовательно, пересмотренный алгоритм предполагает внесение следующих изменений:

• Шаг 1: Разделите набор на... и рекурсивно вычислите расстояние в каждой части, возвращая точки в каждом наборе в отсортированном порядке по y-координате.
• Шаг 4: Объединить два отсортированных списка в один отсортированный список в O(n) время.

Следовательно, в процессе слияния теперь преобладают линейные временные шаги, что дает O(nlogn) алгоритм нахождения ближайшей пары множества точек на плоскости.

Answer 3

Вы можете сэкономить значительную часть времени, сначала проверив, являются ли расстояние вдоль x и y <=, чем последнее сохраненное расстояние (квадрат). Если это правда, то вы продолжаете вычислять расстояние (в квадрате). Конечно, количество сэкономленного вами времени зависит от того, как распределены баллы.