Расстояние от Земли до Юпитера со Skyfield

Question

Я пытаюсь использовать Skyfield, чтобы построить расстояние в ау от Земли до планет Солнечной системы как функцию времени. Это очень просто и даже указано на главной странице пакета. Однако, хотя это отлично работает для ртути, Венеры и Марса, это не работает для других планет. Я не знаком с эфемеридными файлами JPL, но кажется, что, например, у Юпитера нет ключевой записи в файле de421.bsp, которая объясняла бы проблему.

Вот минимальный пример (пример с домашней страницы):

from skyfield.api import load, now

planets = load('de421.bsp')
earth, planet = planets['earth'], planets['jupiter']

jd = now()
position = earth.at(jd).observe(planet)
ra, dec, distance = position.radec()

print(distance)

Ошибка ниже. Обратите внимание, что если вы замените 'jupiter' на 'mars' в приведенном выше коде, он не будет аварийно завершать работу.

---->  earth, planet = planets['earth'], planets['jupiter']
KeyError: "kernel 'de421.bsp' is missing 'JUPITER' - the targets it supports are:
SOLAR SYSTEM BARYCENTER, MERCURY BARYCENTER, VENUS BARYCENTER, EARTH BARYCENTER, 
MARS BARYCENTER, JUPITER BARYCENTER, SATURN BARYCENTER, URANUS BARYCENTER, 
NEPTUNE BARYCENTER, PLUTO BARYCENTER, SUN, MERCURY, VENUS, MOON, EARTH, MARS"

Я неправильно использую файл эфемерид (неправильный барицентр?) Или это всего лишь ограничение файла de421.bsp? Я прочитал описание файла эфемерид на веб-сайте Skyfield ( здесь), но не уверен, что полностью его понял.

Любое предложение о том, как выполнить этот простой расчет расстояния Земля-Юпитер с помощью Skyfield?

Спасибо!

Answer 1

Как говорит ошибка, вам нужно использовать JUPITER BARYCENTER вместо jupiter,

Answer 2

Это просто дополнение, если это полезно - принятый ответ решил проблему.

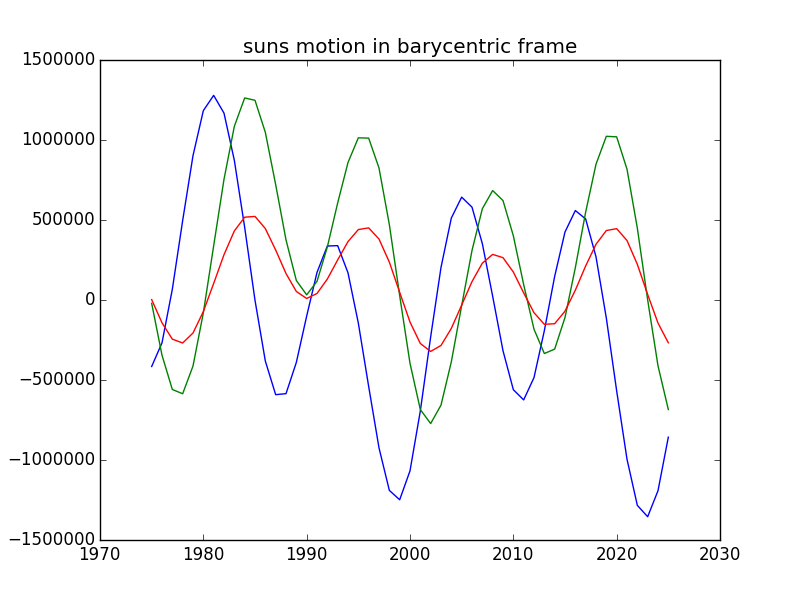
Я хотел показать, что, поскольку позиции находятся в барицентрических координатах, что ['solar system barycenter'] останется в начале координат. Но я был сорван, потому что он возвращает единственное значение ноль, а не вектор (или None). Тем не мение

import matplotlib.pyplot as plt
from skyfield.api import load, JulianDate

data = load('de421.bsp')
sun  = data['sun']
bary = data['solar system barycenter']

years = [1975+i for i in range(51)]
sunpos, barypos = [], []

for year in years:
    jd = JulianDate(utc=(year, 1, 1))
    sunpos.append(sun.at(jd).position.km)
    barypos.append(bary.at(jd).position.km)

plt.figure()
x, y, z = zip(*sunpos)
plt.plot(years, x)
plt.plot(years, y)
plt.plot(years, z)
# x, y, z = zip(*barypos)
# plt.plot(years, x, '-k')
# plt.plot(years, y, '-k')
# plt.plot(years, z, '-k')

plt.title('suns motion in barycentric frame')
plt.savefig('bary one')
plt.show()

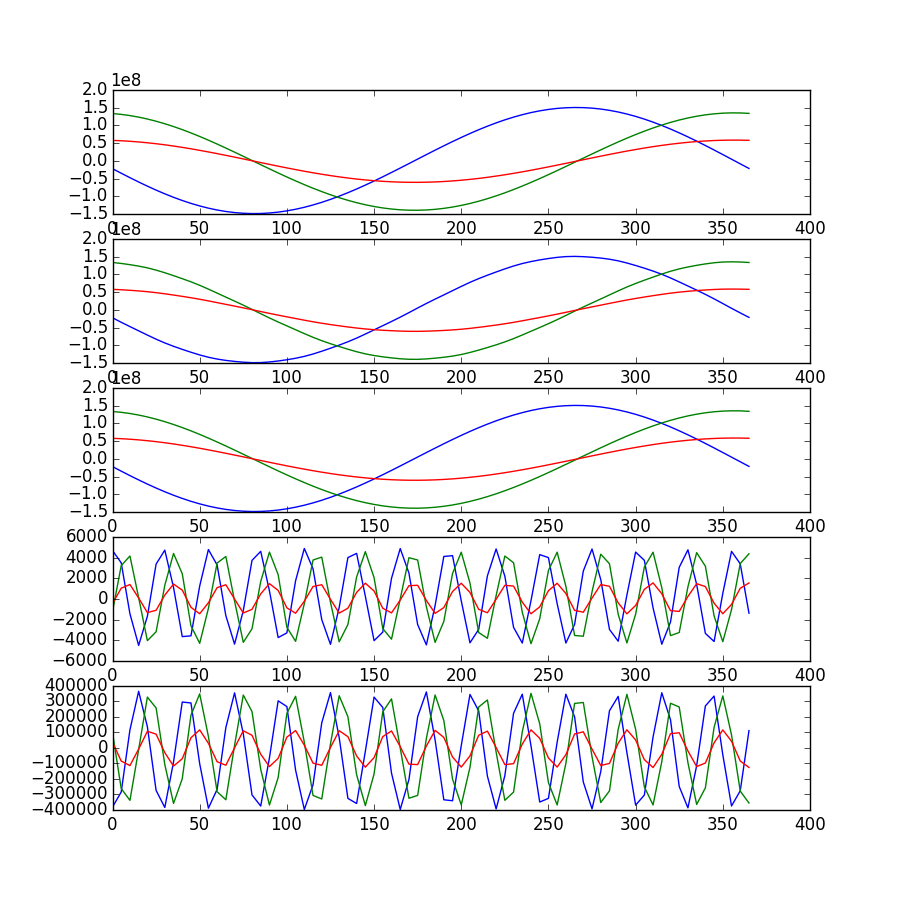
Два нижних графика (ниже) показывают движение Земли и Луны относительно барицентра Земля-Луна, называемое ['earth barycenter'] в Скайфилде:

import matplotlib.pyplot as plt
import numpy as np
from skyfield.api import load, JulianDate

data  = load('de421.bsp')
earth = data['earth']
moon  = data['moon']
bary  = data['earth barycenter']

days = range(0, 366, 5)
earthpos, moonpos, barypos = [], [], []
for day in days:
    jd = JulianDate(utc=(2016, 1, day))  # seems to work
    earthpos.append(earth.at(jd).position.km)
    moonpos.append(moon.at(jd).position.km)
    barypos.append(bary.at(jd).position.km)
ep = np.array(earthpos).T
mp = np.array(moonpos).T
bp = np.array(barypos).T

plt.figure(figsize=[9,9])
plt.subplot(5,1,1)
for thing in ep:
    plt.plot(days, thing)
plt.subplot(5,1,2)
for thing in mp:
    plt.plot(days, thing)
plt.subplot(5,1,3)
for thing in bp:
    plt.plot(days, thing)
plt.subplot(5,1,4)
for thing in (ep-bp):
    plt.plot(days, thing)
plt.subplot(5,1,5)
for thing in (mp-bp):
    plt.plot(days, thing)
plt.savefig('bary two')
plt.show()