Решение рекурсивной последовательности

Question

В последнее время я решал некоторые задачи из Google Foobar для развлечения, и теперь я застрял в одном из них более 4 дней. Речь идет о рекурсивной функции, определенной следующим образом:

R(0) = 1
R(1) = 1
R(2) = 2
R(2n) = R(n) + R(n + 1) + n (for n > 1)
R(2n + 1) = R(n - 1) + R(n) + 1 (for n >= 1)

Задача заключается в написании функции answer(str_S) где str_S является строковым представлением base-10 целого числа S, которое возвращает наибольшее n такой, что R(n) = S, Если такого n нет, верните "None". Кроме того, S будет положительным целым числом не более 10^25.

Я много исследовал о рекурсивных функциях и о решении рекуррентных отношений, но безуспешно. Я вывел первые 500 чисел и не нашел никакого отношения к каждому из них. Я использовал следующий код, который использует рекурсию, поэтому он становится очень медленным, когда числа начинают расти.

def getNumberOfZombits(time):
    if time == 0 or time == 1:
        return 1

    elif time == 2:
        return 2

    else:
        if time % 2 == 0:
            newTime = time/2
            return getNumberOfZombits(newTime) + getNumberOfZombits(newTime+1) + newTime

        else:
            newTime = time/2 # integer, so rounds down
            return getNumberOfZombits(newTime-1) + getNumberOfZombits(newTime) + 1

Задача также включала в себя несколько тестовых случаев, поэтому вот они:

Test cases
==========

Inputs:
    (string) str_S = "7"
Output:
    (string) "4"

Inputs:
    (string) str_S = "100"
Output:
    (string) "None"

Я не знаю, нужно ли мне решить отношение повторения к чему-то более простому, но поскольку есть одно для четных и одно для нечетных чисел, мне действительно трудно это сделать (я еще не узнал об этом в школе, поэтому все, что я знаю об этой теме, из статей в интернете).

Так что любая помощь, которая поможет мне справиться с этой задачей, будет приветствоваться:)

Answer 1

Вместо того чтобы математически упростить эту функцию, я упростил алгоритм в Python. По предложению @LambdaFairy я реализовал памятку в функции getNumberOfZombits(time). Эта оптимизация значительно ускорила работу.

Затем я перешел к следующему шагу, пытаясь выяснить, что послужило причиной для такого количества кроликов. Я анализировал функцию раньше, наблюдая за ее графиком, и я знал, что четные числа сначала получают более высокие результаты, и только через некоторое время нечетные числа достигают того же уровня. Поскольку мы хотим получить максимальный вход для этого выхода, мне сначала нужно было искать в четных числах, а затем в нечетных числах.

Как видите, нечетные числа всегда требуют больше времени, чем четные, чтобы достичь того же результата.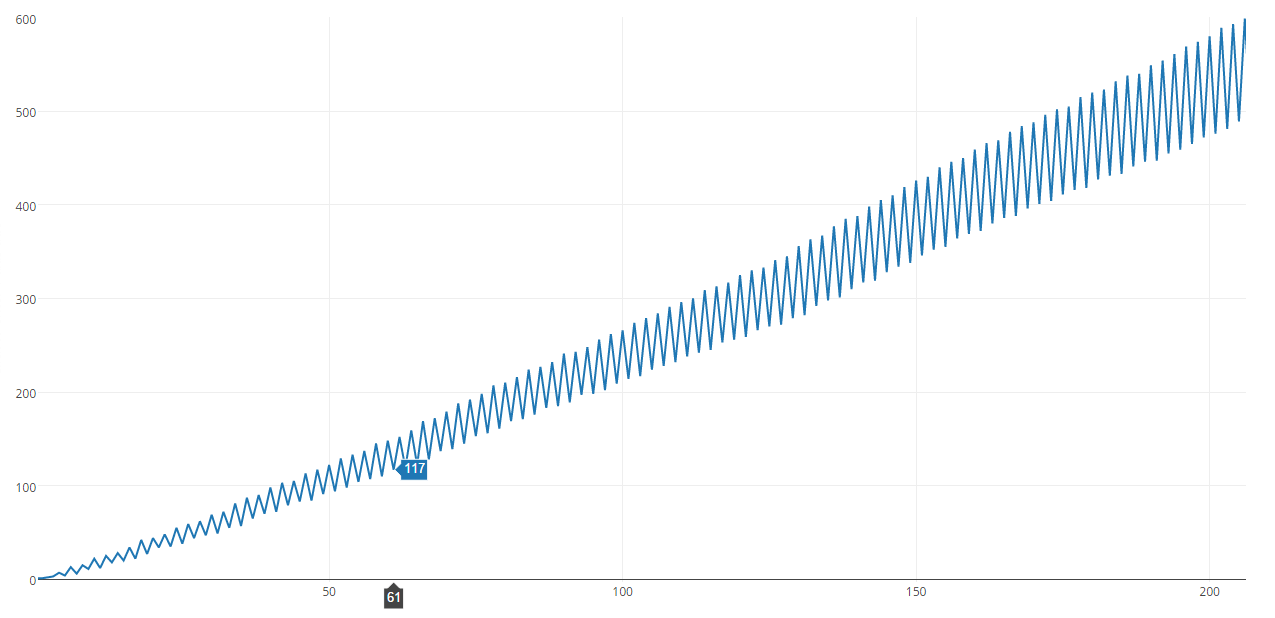

Проблема в том, что мы не могли искать числа, увеличивающиеся на 1 каждый раз (это было слишком медленно). То, что я сделал для решения этой проблемы, заключалось в реализации алгоритма двоичного поиска. Во-первых, я искал четные числа (с помощью алгоритма двоичного поиска), пока не нашел один ответ или у меня не осталось больше чисел для поиска. Затем я проделал то же самое с нечетными числами (опять же, с алгоритмом бинарного поиска) и, если был найден ответ, я заменил на него все, что у меня было раньше (так как он обязательно был больше, чем предыдущий ответ).

У меня есть исходный код, который я использовал для решения этой проблемы, поэтому, если кому-то это нужно, я не против поделиться им:)

Answer 2

Ключом к решению этой загадки было использование бинарного поиска.

Как видно из генераторов последовательностей, они основаны на примерно n/2 рекурсии, поэтому для вычисления R(N) требуется около 2*log2(N) рекурсивных вызовов; и, конечно, вы должны сделать это как для нечетных, так и для четных.

Это не так уж плохо, но вам нужно выяснить, где искать N, который даст вам ввод. Чтобы сделать это, я сначала реализовал поиск верхней и нижней границ для N. Я прошел N вверх по степеням 2, пока у меня не было N и 2N, которые образовали нижнюю и верхнюю границы соответственно для каждой последовательности (нечетной и четной).

С этими границами я мог бы затем выполнить двоичный поиск между ними, чтобы быстро найти значение N или его несуществование.