Сильно компонент

Question

Я пытаюсь написать алгоритм с графом G и двумя узлами "x" и "y" в качестве ввода, который возвращает информацию о том, существует ли циклический путь от "x" до "y"

Является ли хорошей идеей сначала найти сильно связанные компоненты, а затем проверить, принадлежат ли x и y одному и тому же сильно связанному компоненту.
Если они принадлежат разным связным компонентам, скажем, x принадлежит C1, а y принадлежит C2, то если существует путь от C1 до C2, то можно сказать, что существует циклический путь от x до y.

Answer 1

Ваша идея с сильно связанными компонентами должна работать. Вот график и код для эксперимента:

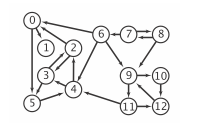
Во-первых, орграф:

И это представление списков смежности:

13 vertices, 22 edges
0: 5 1
1: 
2: 0 3
3: 5 2
4: 3 2
5: 4
6: 9 4 8 0
7: 6 9
8: 6
9: 11 10
10: 12
11: 4 12
12: 9

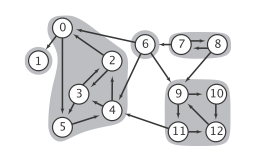
И это сильно связанные компоненты:

7
6 8
9 10 11 12
0 2 3 4 5
1

Теперь, после с реализацией для орграфа и косараю-шарира

class StronglyConnectedComponents
{
    private bool[] visited;
    private int[] componentIds;
    public int ComponentCount { get; private set; }

    public StronglyConnectedComponents(DirectedGraph graph)
    {
        visited = new bool[graph.VertexCount];
        componentIds = new int[graph.VertexCount];

        var order = new GraphTraversal(graph).ReverseOrder();
        var reversedGraph = graph.Reverse();
        foreach (var vertex in order)
        {
            if (!visited[vertex])
            {
                DepthFirstSearch(reversedGraph, vertex);
                ComponentCount++;
            }
        }
    }

    public int VertexComponentId(int vertex)
    {
        return componentIds[vertex];
    }

    public bool AreStronglyConnected(int source, int target)
    {
        return componentIds[source] == componentIds[target];
    }

    private void DepthFirstSearch(DirectedGraph graph, int vertex)
    {
        visited[vertex] = true;
        componentIds[vertex] = ComponentCount;
        foreach (var adjacent in graph.AdjacentTo(vertex))
        {
            if (!visited[adjacent])
            {
                DepthFirstSearch(graph, adjacent);
            }
        }
    }
}

class GraphTraversal
{
    private Stack<int> reversePostOrder;
    private bool[] visited;

    public GraphTraversal(DirectedGraph graph)
    {
        visited = new bool[graph.VertexCount];
        reversePostOrder = new Stack<int>();

        for (var vertex = 0; vertex < graph.VertexCount; vertex++)
        {
            if (!visited[vertex])
            {
                DepthFirstSearch(graph, vertex);
            }
        }
    }

    public IEnumerable<int> ReverseOrder()
    {
        return reversePostOrder;
    }

    private void DepthFirstSearch(DirectedGraph graph, int vertex)
    {
        visited[vertex] = true;
        foreach (var adjacent in graph.AdjacentTo(vertex))
        {
            if (!visited[adjacent])
            {
                DepthFirstSearch(graph, adjacent);
            }
        }
        reversePostOrder.Push(vertex);
    }
}

class DirectedGraph
{
    public int VertexCount { get; set; }
    public int EdgeCount { get; set; } = 0;

    private List<int>[] adjacencyLists;

    public DirectedGraph(int vertexCount)
    {
        VertexCount = vertexCount;
        InitializeAdjacencyLists(vertexCount);
    }

    public void AddEdge(int from, int to)
    {
        adjacencyLists[from].Add(to);
        EdgeCount++;
    }

    public IEnumerable<int> AdjacentTo(int vertex)
    {
        return adjacencyLists[vertex];
    }

    public DirectedGraph Reverse()
    {
        var reversedGraph = new DirectedGraph(this.VertexCount);
        for (var vertex = 0; vertex < this.VertexCount; vertex++)
        {
            foreach (var adjacent in this.AdjacentTo(vertex))
            {
                reversedGraph.AddEdge(adjacent, vertex);
            }
        }
        return reversedGraph;
    }

    public override string ToString()
    {
        String graghString = VertexCount + " vertices, " + EdgeCount + " edges \n";
        for (int vertex = 0; vertex < VertexCount; vertex++)
        {
            graghString += vertex + ": ";
            foreach (var adjacnet in this.AdjacentTo(vertex))
            {
                graghString += adjacnet + " ";
            }
            graghString += "\n";
        }
        return graghString;
    }

    private void InitializeAdjacencyLists(int vertexCount)
    {
        adjacencyLists = new List<int>[vertexCount];
        for (var vertex = 0; vertex < vertexCount; vertex++)
        {
            adjacencyLists[vertex] = new List<int>();
        }
    }
}

Запросы как scc.AreStronglyConnected(2, 5) скажет, существует ли направленный цикл между вершинами. Runnable код здесь.

Answer 2

Я предполагаю, что вы также хотите посчитать пути, имеющие "x" или "y" несколько раз.

Если "x" и "y" принадлежат одному и тому же сильно связанному компоненту, существует путь, содержащий цикл. (тривиально, по определению сильно связной компоненты)

Однако, если они принадлежат к разным сильно связанным компонентам, значение 'y' должно быть достижимым из 'x', и хотя бы один компонент, имеющий узел на пути, должен иметь размер больше одного. (Возьмите любой цикл в этом компоненте и продолжайте путь)

Ваше решение потерпит неудачу в случае линейного графика. Цикла нет, но вы можете перейти от "x" к "y", которые принадлежат различным сильно связанным компонентам.