Python: связанные компоненты на сфере

Question

Я бился головой об этом уже некоторое время. Моя проблема очень проста для объяснения:

У меня есть данные, содержащие долготы и широты. Для простоты предположим, что это координаты городов. Я хочу разделить эти координаты города на группы, чтобы все города в пределах группы находились на заданном "максимальном расстоянии" от ближайшего соседа. У всех городов в группе должен быть хотя бы один сосед в пределах этого ограничения расстояния. Поэтому минимальное расстояние между этими разделенными группами больше, чем "максимальное расстояние", упомянутое выше.

Насколько я понимаю, это проблема кластеризации (например, минимальное связующее дерево). Расстояние на сфере может быть рассчитано с помощью расстояния хаверсин, но я не могу обдумать, как это реализовать... мое ограничение заключается в том, что я могу использовать только numpy, scipy и scikit-learn.

Я надеюсь, что кто-то может помочь, спасибо

Answer 1

Исходя из графического вывода в том виде, в каком оно содержится в вашем ответе, я считаю, что ваши кластеры преждевременно завершаются. Это мой подход к проблеме; код ужасен, потому что на самом деле я просто хотел продемонстрировать концепцию, и у меня нет времени думать о самом элегантном способе проиллюстрировать это. Кроме того, это не просто так, потому что тогда я мог бы украсть мою старую функцию вычисления расстояния, чтобы сэкономить мне время. Надеюсь, что концепция достаточно ясна, и вы увидите, как ее можно сделать быстрее и чище, например, не многократно перестраивая available_locations и, возможно, не повторное сканирование элементов в кластере из предыдущей итерации.

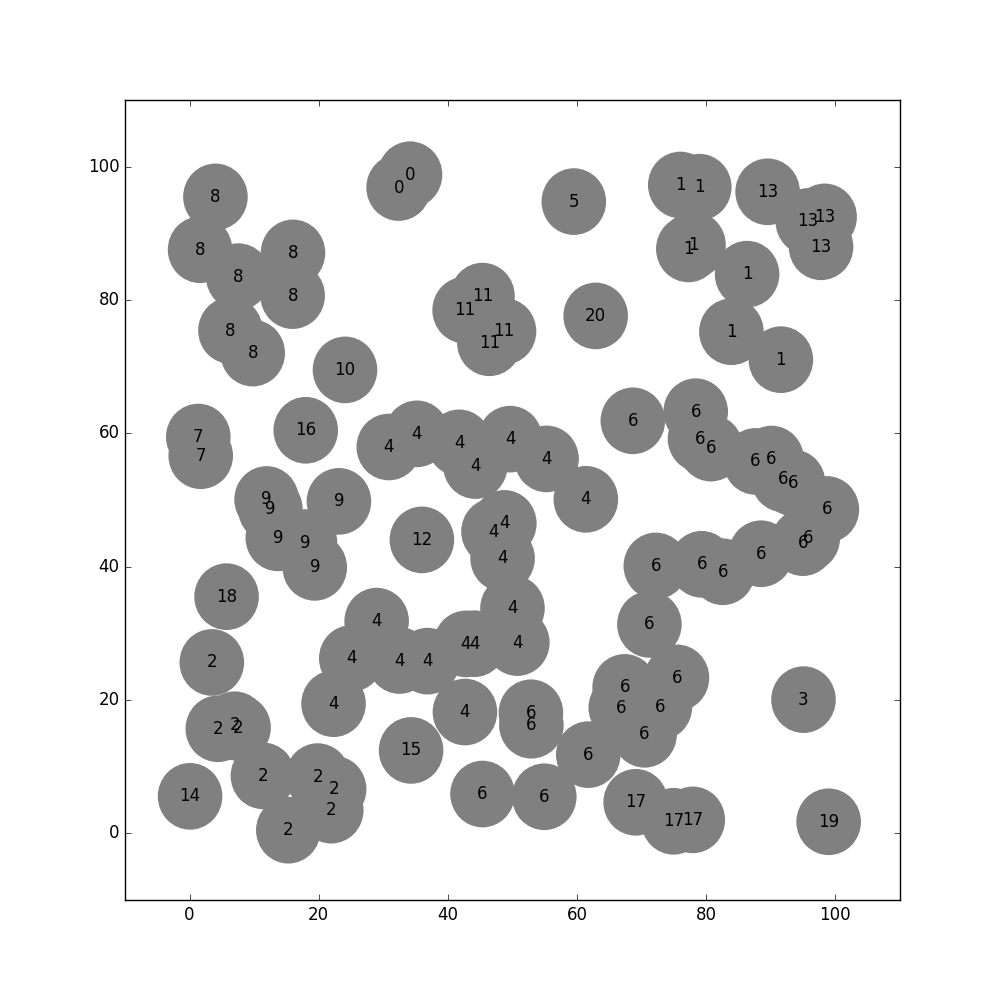
Изменить: Иллюстрированное поведение: 1) Всегда сходится на одном и том же решении для каждого DISTANCE_CAP независимо от всей рандомизации при инициализации и прогрессии решения 2) Модификация DISTANCE_CAP может привести к кластерам в одном месте или гигантской капле

import math
from random import choice, shuffle

DISTANCE_CAP = 20

def crow_flies(lat1, lon1, lat2, lon2):
    dx1,dy1 = (lat1/180)*3.141593,(lon1/180)*3.141593
    dx2,dy2 = (lat2/180)*3.141593,(lon2/180)*3.141593
    dlat,dlon = abs(dx2-dx1),abs(dy2-dy1)
    a = (math.sin(dlat/2))**2 + (math.cos(dx1) * math.cos(dx2) 
        * (math.sin(dlon/2))**2)
    c = 2*(math.atan2(math.sqrt(a),math.sqrt(1-a))) 
    km = 6373 * c
    return km

# Aim: separate these back out
manchester = [[53.486286, -2.251476, 1],
            [53.483586, -2.254534, 2],
            [53.475158, -2.248011, 3],
            [53.397161, -2.509189, 4]]

stoke = [[53.037375, -2.262903, 5],
        [53.031031, -2.199587, 6]]

birmingham = [[52.443368, -1.975714, 7],
            [52.429641, -1.902849, 8],
            [52.483326, -1.817483, 9]]

# Mix them all together
combined_list = [item for item in manchester]
for item in stoke:
    combined_list.append(item)

for item in birmingham:
    combined_list.append(item)

shuffle(combined_list)

# Build a matrix:
matrix = {}
for item in combined_list:
    for pair_item in combined_list:
        if item[2] != pair_item[2]:
            distance = crow_flies(item[0], item[1], pair_item[0], pair_item[1])
            matrix[(item[2], pair_item[2])] = distance

# pick a random starting location
available_locations = [combined_list[x][2] for x in range(len(combined_list))]
start_loc = choice(available_locations)
available_locations = [a for a in available_locations if a != start_loc]

all_clusters = []
single_cluster = []
single_cluster.append(start_loc)

# RECURSIVELY add items to our cluster until it cannot get larger, then start a 
# new one
cluster_got_bigger = True
while available_locations:
    if cluster_got_bigger == True:
        cluster_got_bigger = False
        for loc in single_cluster:
            for item in available_locations:
                distance = matrix[(loc, item)]
                if distance < DISTANCE_CAP:
                    single_cluster.append(item)
                    available_locations = [a for a in available_locations if a != item]
                    cluster_got_bigger = True

    if cluster_got_bigger == False:
        all_clusters.append(single_cluster)
        single_cluster = []
        new_seed = choice(available_locations)
        single_cluster.append(new_seed)
        available_locations = [a for a in available_locations if a != new_seed]
        cluster_got_bigger = True

    if not available_locations:
        all_clusters.append(single_cluster)

print all_clusters

Answer 2

Итак, я применил метод грубой силы, чтобы решить эту проблему. Я не уверен на 100%, верны ли результаты во всех случаях, хотя... если бы у некоторых из вас было время проверить это, это было бы очень признательно.

import numpy as np
import matplotlib.pyplot as plt


# -------------------------------------------------------------------
def distance_sphere(lon1, lat1, lon2, lat2):

    # Calculate distance on sphere
    return np.degrees(np.arccos(np.sin(np.radians(lat1)) * np.sin(np.radians(lat2)) +
                                np.cos(np.radians(lat1)) * np.cos(np.radians(lat2)) *
                                np.cos(np.radians(lon1 - lon2))))


# -------------------------------------------------------------------
def distance_euclid(lon1, lat1, lon2, lat2):

    # Calculate distance
    return np.sqrt((lon1 - lon2)**2 + (lat1 - lat2)**2)


# -------------------------------------------------------------------
# Maximum allowed distance in degrees
max_distance = 10

# Generate city coordinates
lon_all = np.random.random(100) * 100
lat_all = np.random.random(100) * 100

# Start with as many groups as cities
group = np.arange(len(lon_all))

# Loop over all city coordinates
for lon, lat in zip(lon_all, lat_all):

    # Calculate distance to all other cities
    dis = distance_euclid(lon1=lon, lat1=lat, lon2=lon_all, lat2=lat_all)

    # Get index of those which are within the given limits
    idx = np.where(dis <= max_distance)[0]

    # If there is no other city, we continue
    if len(idx) == 0:
        continue

    # Set common group for all cities within the limits
    for i in idx:
        group[group == group[i]] = min(group[idx])


# Rewrite labels starting with 0
for old, new in zip(set(group), range(len(set(group)))):
    idx = [i for i, j in enumerate(group) if j == old]
    group[idx] = new


# -------------------------------------------------------------------
# Plot results
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=[10, 10])
for g, lon, lat in zip(group, lon_all, lat_all):
    ax.annotate(str(g), xy=(lon, lat), xycoords="data", size=12, ha="center", va="center")
    circ = plt.Circle((lon, lat), radius=max_distance/2, lw=0, color="gray")
    ax.add_patch(circ)
ax.set_xlim(-10, 110)
ax.set_ylim(-10, 110)
plt.show()

Answer 3

Может мой ответ запоздал. Но быстрое решение состоит в том, чтобы построить сетевую структуру данных из ваших городов и получить связанные компоненты вашего графа:

• Каждый город является узлом
• Существует граница между двумя городами, если их расстояние между ними меньше некоторого порога.

Наконец, используйте какой-нибудь сетевой модуль Python (например , NetworkX).

Код будет примерно таким:

      import networkx as nx

graph = nx.Graph()

# Add all vertices (cities) to the graph
for i, city in enumerate(cities):
    graph.add_vertex(i)

# Add edges between cities that lie under a distance threshold
for i, city_one in enumerate(cities):
    for j, city_two in enumerate(cities):
         if j > i:
             link_exists = calculate_distance(city_one, city_two) < threshold
             if link_exists:
                 graph.add_edge(i,j)
# A list of sets, each set has the indices of cities
components = [c for c in sorted(nx.connected_components(G), reverse=False)]

Предполагается , что calculate_distance и пороговое значение известны, первое — это функция, а второе — пороговое значение расстояния.