Объяснение взаимной корреляции и нормализации для шаблона соответствия openCV

Question

Мой босс и я не согласны с тем, что происходит с методом CV_TM_CCORR_NORMED для matchTemplate(); в openCV.

Можете ли вы объяснить, что здесь происходит, особенно аспект квадратного корня этого уравнения.

Answer 1

Корреляция - это сходство двух сигналов, векторов и т. Д. Предположим, у вас есть векторы

 template=[0 1 0 0 1 0 ]   A=[0 1 1 1 0 0] B =[ 1 0 0 0 0 1]  

если вы выполните корреляцию между векторами и шаблоном, чтобы получить более похожий, вы увидите A похож на template больше, чем B потому что 1 помещены в соответствующие индексы. Это означает, что чем больше ненулевых элементов соответствует, тем больше корреляция между векторами.

В полутоновых изображениях значения находятся в диапазоне 0-255. Давайте сделаем это:

template=[10 250 36 30] A=[10 250 36 30] B=[220 251 240 210],

Здесь ясно, что A такой же как template но корреляция между B а также template больше чем A а также templateВ нормализованном кросс-корреляционном денумераторе часть формулы решает эту проблему. Если вы проверите формулу ниже, вы можете увидеть, что для B(x)template будет намного больше, чем A(x)template,

Формула, как указано в документации opencv: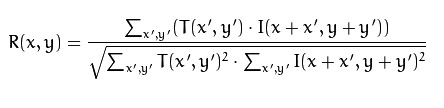

На практике, если вы используете взаимную корреляцию, если в части изображения есть яркость, корреляция между этой частью и вашим шаблоном будет больше. Но если вы используете нормализованную взаимную корреляцию, вы получите лучший результат.

Думаю формула такая:

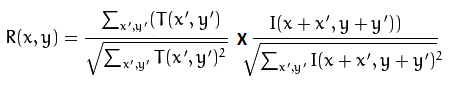
Перед умножением элемента на элемент вы нормализуете две матрицы. Делая корень квадратной суммы всех элементов в матрице, вы удаляете усиление, если все элементы большие, то делитель большой.

Думайте, что вы делите сумму всех элементов в матрице. Если значение пикселя находится в более яркой области, тогда значения пикселей соседей будут высокими. При делении суммы его окрестностей вы удаляете эффект освещения. Это для обработки изображений, где значения пикселей всегда положительны. Но для 2D-матрицы могут быть отрицательные значения, поэтому квадрат игнорирует знак.