Нахождение минимального сечения сети потока
Я пытаюсь найти минимальное сокращение следующей сети 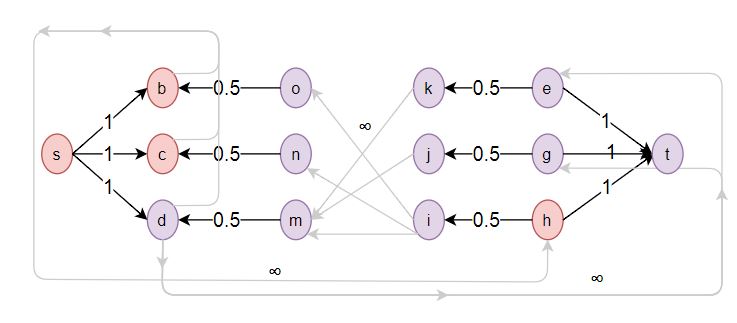
Я использую следующий алгоритм:
Запустите алгоритм Форда-Фулкерсона и рассмотрите окончательный остаточный граф.
Найдите множество вершин, которые достижимы из источника в остаточном графе.
Все ребра, которые находятся от достижимой вершины до недостижимой вершины, являются минимальными отрезанными ребрами. Распечатайте все такие края.
На первом этапе мой алгоритм находит 3 пути:
- s->b->h->t **value: 1**
- s->d->e->t **value: 1**
- s->c->h->i->m->d->g->t **value: 0.5**
Таким образом, максимальный расход (и, следовательно, минимальный срез) равен 2,5.
Однако, когда я позже попытаюсь устранить вышеупомянутые пути из сети, я получу что-то вроде этого: 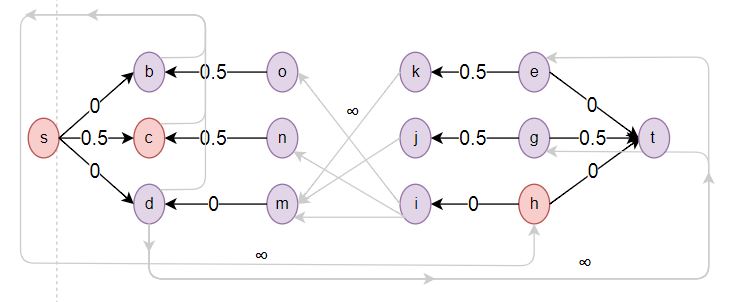
Достижимыми вершинами являются s, c и h, которые образуют разрез, равный 3,5.
Что мне не хватает? Почему я не могу пересечь график, как обычно, чтобы получить минимальное сокращение?
2 ответа
Каждый раз, когда вы увеличиваете емкость ребра в остаточном графе, вам нужно увеличивать емкость противоположного ребра на ту же величину.
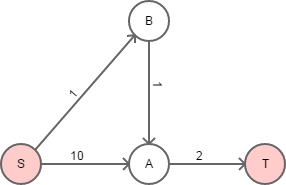
Пример графика:
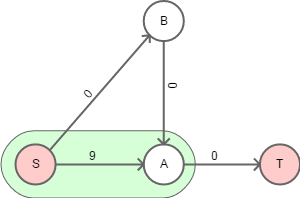
Вот остаточный граф без обратных ребер и множество вершин, достижимых из S (которые не составляют мин-разрез):
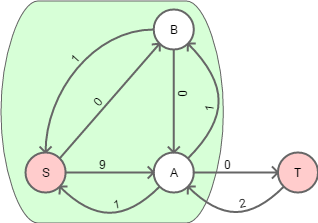
И правильный остаточный граф с мин-разрезом:
Я предполагаю, что ваше определение остаточного графа таково, что вы помещаете ребро A->B в остаточный граф, если:
a) Существует некоторое различие между потоком и пропускной способностью в направлении A->B (он же передний край) b) Существует некоторый поток в направлении B->A (он же задний край)
В этом определении ваш шаг 2 неверен.
Чтобы найти минимальный разрез, вы идете только через передние края от начала. Теперь вы можете обозначить вершины, доступные с начала, как множество R, а остальные как множество R'. Теперь разрез сделан ребрами между R и R'. И размер разреза - это поток между R и R'.