Формулирование экспоненциального уравнения с учетом определенной пары точек
У меня есть следующие пары очков:
(0, 100); (0,81, 41); (1,38, 20); (1,75, 9); (2, 4)
Как я могу определить уравнение кривой, проходящей через эту точку?
Спасибо большое!
ОБНОВИТЬ
Я пытаюсь добиться того, чтобы функция, представленная на рисунке, показала уменьшение высоты.
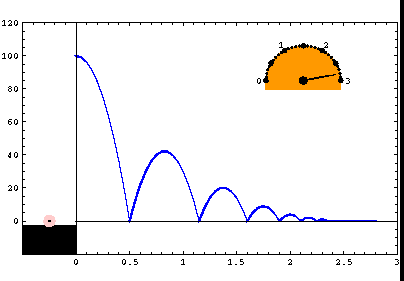
4 ответа
Через эти точки проходит бесконечно много кривых. Вы должны быть более конкретным.
Если вы хотите, чтобы через них проходил полином минимальной степени, вы можете использовать интерполяционный полином Лагранжа.
На вашем примере это будет полином степени 4. Но, как я уже сказал, если вы допустите более высокие степени, вы получите бесконечно много результатов.
Вы можете использовать множество представлений, в зависимости от ваших требований к преемственности в каждой точке.
Кусочно-линейные сегменты будут "работать", но вы также можете использовать кусочные интерполяции более высокого порядка. Вы можете использовать Безье или другую технику сплайнов.
Вы можете принять один полином порядка 4 и рассчитать коэффициенты, чтобы он проходил через каждую точку.
Есть много способов сделать это.
Я нашел этот сайт, который, кажется, именно то, что мне нужно. Я просто должен ввести свои пары данных и выбрать соответствующую степень (в моем случае 4). Затем он вычисляет коэффициент корреляции и уравнение.
Если ваши данные x_i,y_i (i=1..n), вы можете поместить строку через x_i,log(y_i); если эта строка - log(y_i) ~ a*x_i + b, то x->exp(b)*exp(a*x) вполне может соответствовать исходным данным.