Наименьшее расстояние между точкой и траекторией
Для гео-онлайн-игры я ищу алгоритм, который находит кратчайшее расстояние между указанной точкой и известным путем, соединенным координатами x/y, чтобы я мог убить все лишние точки / узлы. Ссылка или ключевое слово для этого алгоритма очень мне помогут! Спасибо за прочтение
Для лучшего понимания: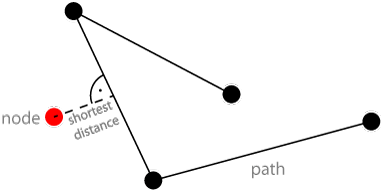
3 ответа
Вы хотите рассчитать это для того, чтобы сказать что-то вроде "если расстояние от точки до пути равно нулю, то удалить точку"? Если это так, то, вероятно, существует более простой способ удаления избыточных узлов. Возьмите три очка за раз (позвоните им A, B, а также C). Рассчитать угол между A а также Bа также угол между B а также C, Если два угла одинаковы, то укажите B лежит на пути между A а также C и является излишним. Вы можете использовать функцию "atan2" (или эквивалент вашего языка) для вычисления углов.
Это моя реализация Java для ближайшей точки на пути
private Point getNearestPoint(Point from, List<Point> to_path) {
int count = to_path.size();
if (count == 0)
return null;
if (count == 1)
return to_path.get(0);
double nearest_dist = Double.MAX_VALUE;
Point nearest_point = null;
for (int i = 1; i < count; i++) {
Point p1 = to_path.get(i-1);
Point p2 = to_path.get(i);
Point p = getNearestPointOnSegment(from, p1, p2);
if (p != nearest_point) {
double dist = dist(from, p);
if (dist < nearest_dist) {
nearest_dist = dist;
nearest_point = p;
}
}
}
return nearest_point;
}
private Point getNearestPointOnSegment(Point from, Point p1, Point p2) {
if (dist(p1, p2) < 1e3) {
Log.d(TAG, "Points are near");
return p1;
}
double d2 = dist2(p1, p2);
double t = ((from.x - p1.x) * (p2.x - p1.x) + (from.y - p1.y) * (p2.y - p1.y)) / d2;
if (t < 0) {
//Log.d(TAG, "p1");
return p1;
}
if (t > 1) {
//Log.d(TAG, "p2");
return p2;
}
//Log.d(TAG, "t:" + t);
return new Point((int)(p1.x + t * (p2.x - p1.x)),
(int)(p1.y + t * (p2.y - p1.y)));
}
private double dist(Point p1, Point p2) {
return Math.sqrt(dist2(p1, p2));
}
private double dist2(Point p1, Point p2) {
return sqr(p1.x - p2.x) + sqr(p1.y - p2.y);
}
private double sqr(double x) {
return x * x;
}
Это двухточечный алгоритм поиска пути, который обычно используется в играх:
Возможно, вам придется применять его несколько раз между вашей точкой и траекторией, но обычно это очень быстро. Алгоритм имеет некоторые оптимизации для сеток карты (где расстояния между квадратами являются целыми числами). Это описание можно найти в: Программирование в реальном времени для стратегической игры с использованием MS DirectX 6.0 от Микки Кавика.
Алгоритм Джикстры - это хороший алгоритм поиска пути общего назначения от одного исходного узла ко всем остальным узлам графа. Вы можете остановить алгоритм, когда вы нашли то, что вам нужно - что в вашем случае было бы, когда алгоритм нашел кратчайший путь к каждому узлу на пути.
Я не знаю определенного алгоритма "кратчайшего пути от узла к пути".