Балансировка дерева AVL
У меня возникли проблемы с вопросом о балансирующем дереве AVL, поскольку мое решение конфликтует с решением из учебника. Я посмотрел на онлайн визуализации деревьев AVL, и они предполагают, что мое правильно. Мой учебник не так?
Затем я должен вставить 65 в это дерево AVL. Это вызывает дисбаланс, и, насколько я понимаю, требуется вращение вправо.
Вот то, что я придумал, и подтвердил через http://robinsswei.github.io/VisGraphs/avltree.html: 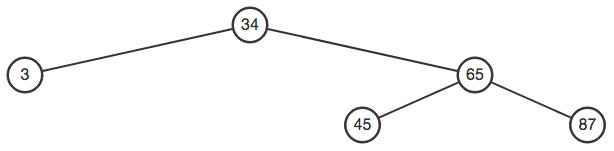
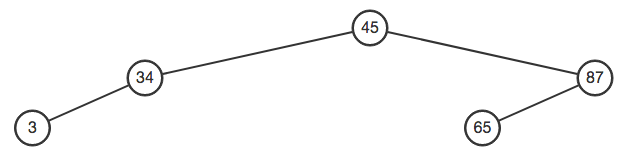
И вот что мой учебник утверждает, что правильный ответ:
Какой из них правильный ответ?
2 ответа
Привет, я на самом деле думаю, что оба решения верны. Я думаю, что есть только несколько причин, по которым ваша книга может отличаться. После вставки узла вы обнаружите, что 2 разных узла имеют коэффициент баланса двух. Это были узлы 34 и 45. Принцип работы этого алгоритма - после вставки. Из этого следует, что путь обратно к корневому узлу проверяет коэффициенты баланса, а также обновляет их высоту. Я думаю, потому что корень был последним, к которому обращались и отмечали для вращения, поэтому он сделал это таким образом. Другая потенциальная причина заключается в том, что для корневого узла вращение требует только простого вращения, тогда как для того, что вы сделали, требуется двойное вращение. Несмотря на это, я чувствую, что оба ответа адекватны.
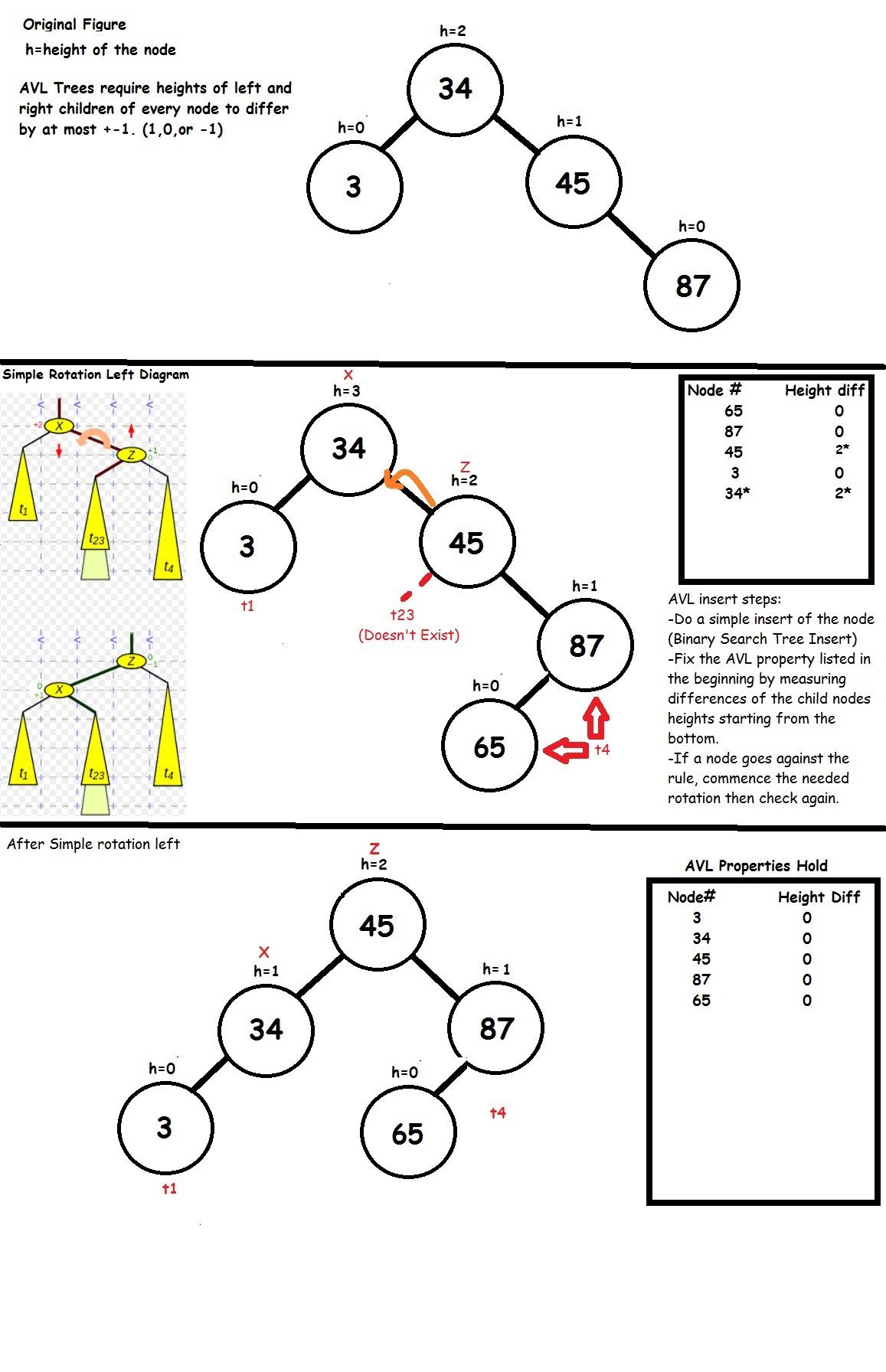
Я попытаюсь объяснить эту проблему для тех, кто может не знать, что такое деревья AVL. Я также попытался обозначить это иллюстрацией. Первое, что вы хотите сделать, это убедиться, что ваше начальное дерево AVL соответствует требованиям, прежде чем вставлять новый узел. Я бы просто обозначил высоту каждого узла, а затем получил бы разницы высот ваших дочерних узлов для каждого родителя.
Деревьям AVL требуется, чтобы высота левого и правого потомка каждого узла отличалась не более чем на +1 или -1. (-1,0,1)
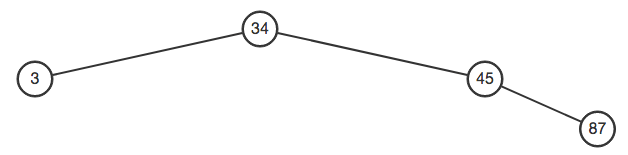
Например, на первом рисунке перед вставкой Id начинается снизу вверх. У узла 87 нет детей, для этого было бы 0. У узла 45 есть только один ребенок, поэтому мы считаем, что рост 87 равен 0. Узел 3 не имеет детей, так что это тоже будет 0. Узел 34 имеет двоих дочерних элементов, 3 и 45. Их разница составляет всего 1. Все узлы прошли тест дерева AVL.
Затем просто вставьте узел, пройдя его, как дерево двоичного поиска.
После вставки пометьте высоту ваших узлов и сравните их снова для каждого узла. На этот раз мы видим, что узел 34 (наш корневой узел) имеет разницу "2" между детьми (2-0). Теперь мы знаем, что вращение необходимо для узла 34.
Выполнено простое вращение влево и свойства AVL были соблюдены.
Второй с корнем 45 является правильным ответом. Сбалансированное дерево AVL должно иметь одинаковую длину (глубину) дочерних элементов. Поэтому после ввода 65 ваше дерево будет неуравновешенным. Так что вам нужно сместить узел влево.
Я думаю, что это должно быть вращение вправо-вправо вместо вращения вправо-влево, чтобы учебник был правильным.