Как генерировать хаотические последовательности из гиперхаотической системы Чена?

Question

Мне нужно сгенерировать две хаотические последовательности на основе гиперхаотической системы Чена. Это должно быть сгенерировано из следующих четырех формул

X=ay-x;
Y=-xz+dx+cy-q;
Y=xy-bz;
Q=x+k;

где a,b,c,d,x,y,z,q все инициализируются следующим образом. Мне нужны только X и Y где

  X=[x1,x2,...x4n]
  Y=[y1,y2,...y4n]
  a=36 ;
  b=3 ;
  c=28 ;
  d=16 ;
  k=0.2 ;
  x=0.3 ;
  y=-0.4 ;
  z=1.2 ;
  q=1 ;
  n=256 ;

Я попробовал следующий код, но я не могу получить его правильно.

clc

clear all

close all

w=imread('C:\Users\Desktop\a.png');

[m n]=size(w)

a=36;

b=3;

c=28;

d=16;

k=0.2;

x(1)=0.3;

y(1)=-0.4;

z(1)=1.2;

q(1)=1;

for i=1:1:4(n)

  x(i+1)=(a*(y(i)-x(i)));

  y(i+1)=-(x(i)*z(i))+(d*x(i))+(c*y(i))-q(i);

  z(i+1)=(x(i)*y(i))-(b*z(i));

  q(i+1)=x(i)+k;

end

disp(x);

disp(y);

Пожалуйста, помогите. заранее спасибо.

Answer 1

Ваш код даже близко не подходит к тому, что вы хотите. К счастью, я смутно интересуюсь этой проблемой, и у меня есть куча свободного времени, поэтому я подумал, что постараюсь реализовать ее шаг за шагом, чтобы показать вам, что делать. Я оставил несколько пробелов для вас, чтобы заполнить.

Похоже, вы хотите интегрировать систему гиперхаотического чена, которая имеет различные определения в Интернете, но вы, кажется, сосредоточены на

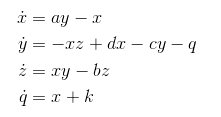
Итак, давайте напишем функцию Matlab, которая определяет эту систему

function vdot = chen(t, v, a, b, c, d, k)

    % Here you unpack the input vector v -
    x = v(1); y = v(2); z = v(3); q = v(4);

    % Here you need to implement your equations as xdot, ydot etc.
    %   xdot = ...
    %   ydot = ...
    % I'll leave that for you to do yourself.

    % Then you pack them up into an output vector -
    vdot = [xdot; ydot; zdot; qdot];

end

Сохраните это в файле с именем chen.m, Теперь вам нужно определить значения параметров a, b, c, d и k, а также ваше начальное условие.

% You need to define the values of a, b, c, d, k here.
%    a = ...
%    b = ...
% You also need to define the vector v0, which is a 4x1 vector of your
% initial conditions
%    v0 = ...
%

Следующая строка создает функцию, которая может использоваться процедурами интеграции Matlab. Первый параметр t текущее время (которое вы на самом деле не используете), а второй параметр 4x1 вектор, содержащий x, y, z, q.

>> fun = @(t,v) chen(t,v,a,b,c,d,k)

Теперь вы можете использовать ode45 (который выполняет численное интегрирование с использованием схемы Рунге-Кутта 4-го порядка), чтобы интегрировать ее и построить некоторые пути. Первый аргумент ode45 это функция, которую вы хотите интегрировать, второй аргумент - это интервал времени, по которому нужно интегрировать (я решил интегрировать от 0 до 100, может быть, вы хотите сделать что-то другое), а третий аргумент - это ваше начальное условие (которое, надеюсь, вы уже определены).

>> [t, v] = ode45(fun, [0 100], v0);

Выходы t, вектор раз и v, которая будет матрицей, столбцы которой представляют собой разные компоненты (x, y, z, q), а строки - значения компонентов в каждый момент времени. Таким образом, вы можете вытащить столбец для каждого из компонентов x и y и построить их

>> x = v(:,1);
>> y = v(:,2);
>> plot(x,y)

Что дает довольно хаотично выглядящий сюжет:

Answer 2

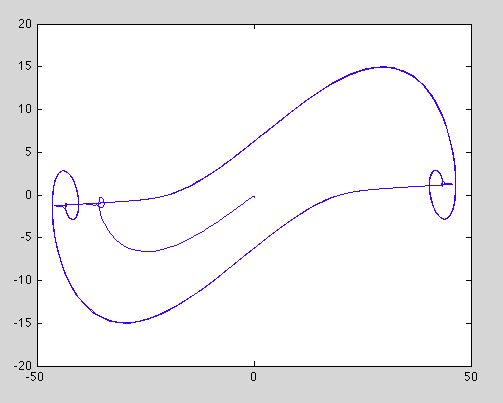
@Abirami Anbalagan и сэр @Chris Taylor, я также до некоторой степени изучал гиперхаотическую систему. По моему мнению, для того, чтобы система была хаотичной, значения должны быть как a= 35; б = 3; с = 12; д = 7; v(n) = [-422 -274 0 -2,4] транспонировать, где v (n) - матрица 4*1.