Может ли сортировка быть P, NP и NP-Complete?
Я очень смущен, и это моя мысль после некоторого прочтения:
P находится в NP, а NP находится в NP-Complete. Следовательно, все P могут быть в NP и NP-Complete?
Означает ли это, что существуют алгоритмы сортировки, которые могут быть NP и NP-Complete?
Надеюсь, это не звучит слишком глупо.
2 ответа
Перво-наперво:
P находится в NP; NP находится в NP-Complete. следовательно, все P может быть в NP и NP-Complete?
Это довольно утверждение, потому что то, что вы говорите, подразумевает P = NP. Никто не смог доказать это или нет. Итак, вот как обстоят дела:
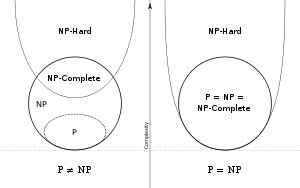
Большинство людей считают, что P!=NP. Цитата из Википедии:
В опросе 2002 года, в котором приняли участие 100 исследователей, 61 полагал, что ответом будет "нет", 9 - "да", а 22 - не уверены; Я полагаю, что этот вопрос может быть независимым от принятых в настоящее время аксиом и поэтому его невозможно доказать или опровергнуть.
Простой способ понять это: предположим, вам дано решение какой-то проблемы. Если вы можете проверить, является ли решение правильным или нет за полиномиальное время, то проблема в NP. Ясно, что каждая задача, которая может быть решена за полиномиальное время (P), находится в NP. Сейчас у нас есть несколько проблем, которые могут быть проверены за полиномиальное время, но не могут быть решены за одно и то же время. Мы не уверены в том, что когда-либо не может быть решения за полиномиальное время или мы пока не можем его выяснить.
Сортировка чисел
Учитывая список чисел, вы можете проверить, отсортирован ли список за полиномиальное время или нет, поэтому проблема явно в NP.
Известны алгоритмы сортировки списка чисел за полиномиальное время. (Пузырьковая сортировка O(n^2) и т. Д.). Таким образом, проблема в P.
Надеюсь это поможет.
Вы можете прочитать этот блог.
P, NP, NP-hard и NP-complete - классы сложности задач; они характеризуют проблему, а не алгоритм.