Java 8 Лямбда-выражения для решения фибоначчи (нерекурсивный способ)
Я новичок в использовании функции лямбда-выражений в Java 8. Лямбда-выражения довольно полезны при решении таких программ, как проверка простых чисел, факториал и т. Д.
Однако они могут быть эффективно использованы при решении таких задач, как Фибоначчи, где текущее значение зависит от суммы двух предыдущих значений. Я довольно хорошо решил проблему проверки простых чисел, эффективно используя лямбда-выражения. Код для того же приведен ниже.
boolean checkPrime=n>1 && LongStream.range(2, (long) Math.sqrt(n)).parallel().noneMatch(e->(n)%e==0);
В приведенном выше коде в noneMatch метод, который мы оцениваем с текущим значением (e) В диапазоне. Но для задачи Фибоначчи нам нужны предыдущие два значения.
Как мы можем сделать это?
9 ответов
Самое простое решение - использовать поток Pairs:
Stream.iterate(new long[]{ 1, 1 }, p->new long[]{ p[1], p[0]+p[1] })
.limit(92).forEach(p->System.out.println(p[0]));
Из-за отсутствия стандартного типа пары используется массив из двух элементов. Далее я пользуюсь .limit(92) так как мы не можем оценить больше элементов, используя long ценности. Но это легко адаптироваться к BigInteger:
Stream.iterate(new BigInteger[]{ BigInteger.ONE, BigInteger.ONE },
p->new BigInteger[]{ p[1], p[0].add(p[1]) })
.forEach(p->System.out.println(p[0]));
Это будет работать до тех пор, пока у вас не будет достаточно памяти для представления следующего значения.
Кстати, чтобы получить n-й элемент из потока:
Stream.iterate(new long[]{1, 1}, p -> new long[]{p[1], p[0] + p[1]})
.limit(91).skip(90).findFirst().get()[1];
Чтобы получить N-й элемент Фибоначчи (используя сокращение):
Stream.iterate(new long[] {1, 1}, f -> new long[] {f[1], f[0] + f[1]})
.limit(n)
.reduce((a, b) -> b)
.get()[0];
решение фибоначчи (не рекурсивный способ)
Это не произойдет с вашим подходом
Генерация чисел Фибоначчи на основе предыдущих двух чисел основана на предыдущих двух числах, т.е. это рекурсивный алгоритм, даже если вы реализуете его без рекурсии, но в цикле.
Существуют другие способы, основанные на экспоненциальной матрице, так что вы можете вычислить n-е число Фибоначчи без вычисления n-1 предыдущих чисел, но для вашей задачи (вычисления ряда) это не имеет смысла.
Итак, чтобы ответить на ваш вопрос в конце, а именно, как я могу использовать лямбда-выражения для двух предыдущих элементов?: иметь список кортежей, каждый из которых содержит два последовательных числа, и повторять их, добавляя новый кортеж на каждом шаге.
Если вы хотите, чтобы нерекурсивная реализация нашла n-й номер последовательности Фибоначчи, вы можете использовать формулу:
Un = ( (1+sqrt(5))^n - (1-sqrt(5))^n ) / (2^n * sqrt(5))
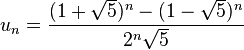
long fibonacci(int n) {
return (long) ((Math.pow(1 + Math.sqrt(5), n) - Math.pow(1 - Math.sqrt(5), n)) /
(Math.pow(2, n) * Math.sqrt(5)));
}
Вы можете использовать переменную в своем лямбда-выражении, чтобы временно сохранить предыдущий элемент, который необходим для вычисления следующего элемента в последовательности Фибоначчи.
public class FibonacciGenerator {
private long prev=0;
public void printSequence(int elements) {
LongStream.iterate(1, n -> {n+=prev; prev=n-prev; return n;}).
limit(elements).forEach(System.out::println);
}
}
Обычно метод и поле лучше объявляются как статические, но я хотел показать, что можно использовать и поля экземпляра.
Обратите внимание, что вы не можете использовать локальную переменную (объявленную в методе или переданную в метод) вместо поля, поскольку такие переменные должны быть окончательными, чтобы использовать их в лямбдах. Для нашей цели нам нужна изменяемая переменная для хранения различных значений во время итерации.
Я знаю, что это старый вопрос, но я считаю, что стоит добавить еще несколько способов добиться успеха, используя
Pair<> и я придумал 2 способа добиться использования
Stream API.
//calculate Fibonacci at given place
public static long fibonacciAt(int place) {
Pair<Integer, Integer> seed = new Pair<>(0, 1);
//return Stream.iterate(seed, feed -> new Pair<>(feed.getValue(), feed.getValue() + feed.getKey())).limit(place).reduce((integerIntegerPair, integerIntegerPair2) -> integerIntegerPair2).orElse(seed).getValue();
return Stream.iterate(seed, feed -> new Pair<>(feed.getValue(), feed.getValue() + feed.getKey())).limit(place).skip(place-1).findFirst().orElse(seed).getValue();
}
Комментированный оператор возврата также отлично работает, который использует
reduce.
Более поздний оператор return пропускает количество пар до
place переменной.(Это потому, что у нас нет
findLast() метод).
Используя Stream.generat(), мы можем сделать следующее:
int[] fie ={0,1};
Stream.generate(() -> {
int r = fie[1];
int f3 = fie[0] + fie[1];
fie[0] = fie[1];
fie[1] = f3;
System.out.println(r);
return r;
}).limit(40)
.collect((Collectors.toList()));
Вы можете рассматривать вычисление n-го числа Фибоначчи как редукцию с двумя предыдущими элементами вместо одного, что типично.
Вот код:
public static long fibonacciByStream(int n) {
long[] results = IntStream.rangeClosed(3, n)
.boxed()
.reduce(new long[]{0, 1, 1},
(fib, i) -> {
fib[i % 3] = fib[(i - 2) % 3] + fib[(i - 1) % 3];
return fib;
},
(a, b) -> null);
return results[n % 3];
}
Однако это решение выглядит проще без какого-либо потока:
public static long fibonacciByLoop(int n) {
long[] fib = new long[]{0, 1, 1};
for (int i = 3; i <= n; i++) {
fib[i % 3] = fib[(i - 2) % 3] + fib[(i - 1) % 3];
}
return fib[n % 3];
}
Примечания:
- Я считаю 0 0-м числом Фибоначчи, потому что это упрощает код.
- Я использовал массив с тремя элементами вместо двух, потому что его легче понять.
- Я использовал «(a, b) -> null» в качестве объединителя, потому что он не используется в последовательном потоке.
- Я опустил проверку, не является ли n отрицательным.
Stream.Iterate(new Integer[] { 0, 1 }, p -> new Integer[] { p[1], p[0] + p[1] })
.map(p -> p[0].to String())
.limit(6)
.collect(Collectors. Joining(","));