Может кто-нибудь рассказать мне о алгоритме поиска kNN, который использует Matlab?
Я написал базовый алгоритм O(n^2) для поиска ближайшего соседа. Как обычно, метод knnsearch (..) в Matlab 2013a работает намного быстрее.
Может кто-нибудь сказать мне, какую оптимизацию они использовали в своей реализации?
Я в порядке с чтением любой документации или бумаги, на которую вы можете указать мне.
PS: я понимаю, что документация на сайте упоминает статью о kd-деревьях в качестве ссылки. Но, насколько я понимаю, kd-деревья - это опция по умолчанию, когда номер столбца меньше 10. Мой - 21. Поправьте меня, если я ошибаюсь.
2 ответа
Самая большая оптимизация, которую MathWorks осуществил при реализации поиска ближайших соседей, заключается в том, что все сложные вещи реализованы в MEX-файле, как скомпилированный C, а не MATLAB.
С таким алгоритмом, как kNN, который (в моем ограниченном понимании) является достаточно рекурсивным и сложным для векторизации, это, вероятно, даст такое улучшение, что анализ O() будет релевантным только на довольно высоком уровне. n,
Более подробно, под капотом knnsearch команда использует createns создать NeighborSearcher объект. По умолчанию, когда X имеет менее 10 столбцов, это будет KDTreeSearcher объект и когда X имеет более 10 столбцов, это будет ExhaustiveSearcher объект (оба KDTreeSearcher а также ExhaustiveSearcher подклассы NeighborSearcher).
Все объекты класса NeighbourSearcher есть метод knnsearch (который вы бы редко вызывали напрямую, используя вместо этого удобную команду knnsearch а не этот метод). knnsearch метод KDTreeSearcher звонки прямо в MEX файл для всей тяжелой работы. Это находится в matlabroot \ toolbox \ stats \ stats \ @KDTreeSearcher \ private \ knnsearchmex.mexw64.
Насколько я знаю, этот MEX-файл в значительной степени выполняет алгоритм, описанный в статье Фридмана, Бентели и Финкеля, на которую ссылается страница документации, без каких-либо структурных изменений. Как следует из названия статьи, этот алгоритм O(log(n)), а не O(n^2). К сожалению, содержимое файла MEX недоступно для проверки, чтобы подтвердить это.
Код создает структуру разбиения пространства KD-дерева для ускорения поиска ближайшего соседа, думая о ней как о создании индексов, обычно используемых в RDBMS для ускорения операций поиска.
В дополнение к поиску ближайших соседей эта структура также ускоряет поиск по дальности, который находит все точки, находящиеся на расстоянии r из точки запроса.
Как указывает @SamRoberts, ядро кода реализовано в C/C++ как MEX-функция.
Обратите внимание, что knnsearch выбирает построение KD-дерева только при определенных условиях и в противном случае возвращается к исчерпывающему поиску (путем наивного поиска во всех точках ближайшего).
Имейте в виду, что в случае очень многомерных данных (и нескольких случаев) алгоритм вырождается и не лучше, чем исчерпывающий поиск. В общем, как вы идете с размерами d>30стоимость поиска KD-деревьев увеличится до поиска почти всех точек и может даже стать хуже, чем поиск методом грубой силы из-за накладных расходов, связанных с созданием дерева.
Существуют и другие варианты алгоритма, который имеет дело с большими измерениями, такими как деревья шаров, которые разделяют данные на ряд вложенных гипер-сфер (в отличие от разделения данных вдоль декартовых осей, таких как KD-деревья). К сожалению, они не реализованы в официальном наборе инструментов статистики. Если вы заинтересованы, вот статья, которая представляет обзор доступных алгоритмов kNN.
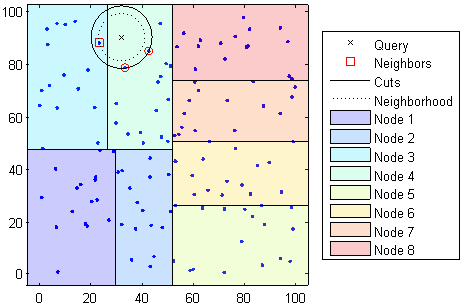
(Выше приведен пример поиска разделенного 2d пространства дерева kd, заимствованного из документации)