Найти кратчайшее расстояние между точкой и отрезками (не линиями)
У меня есть набор отрезков (не линий), (A1, B1), (A2, B2), (A3, B3), где A,B являются конечными точками отрезка. каждый A а также B имеет (x,y) координаты.
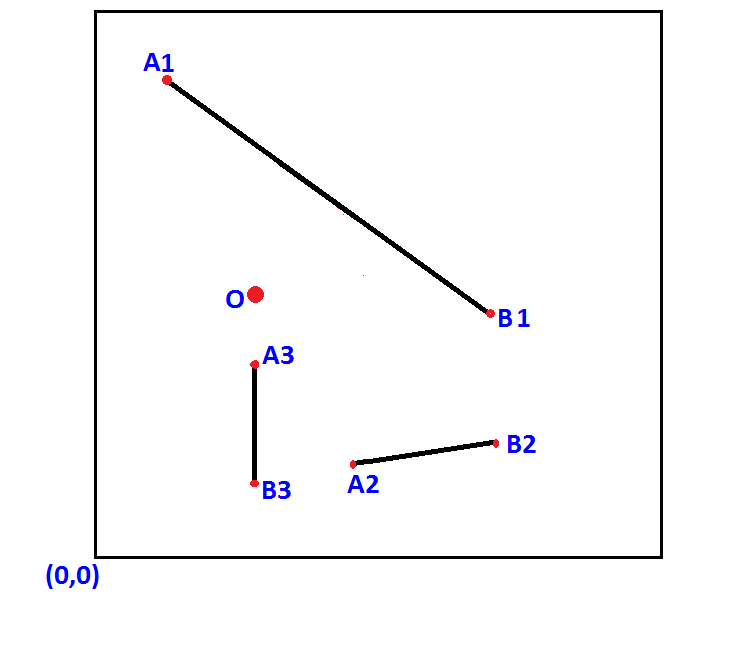
ВОПРОС: Мне нужно знать кратчайшее расстояние между point O а также line segments как показано на показанном рисунке, реализовано в виде строки кодов. Код, который я действительно могу понять, это либо псевдокод, либо Python.
КОД: Я пытался решить проблему с этим кодом, к сожалению, он не работает должным образом.
def dist(A, B, O):
A_ = complex(*A)
B_ = complex(*B)
O_= complex(*O)
OA = O_ - A_
OB = O_ - B_
return min(OA, OB)
# coordinates are given
A1, B1 = [1, 8], [6,4]
A2, B2 = [3,1], [5,2]
A3, B3 = [2,3], [2, 1]
O = [2, 5]
A = [A1, A2, A3]
B = [B1, B2, B3]
print [ dist(i, j, O) for i, j in zip(A, B)]
Заранее спасибо.
5 ответов
Вот ответ. Этот код принадлежит Малкольму Кессону, источник здесь. Я предоставил это прежде только с самой ссылкой, и это было удалено модератором. Я предполагаю, что причина этого в том, что не предоставили код (как ответ).
import math
def dot(v,w):
x,y,z = v
X,Y,Z = w
return x*X + y*Y + z*Z
def length(v):
x,y,z = v
return math.sqrt(x*x + y*y + z*z)
def vector(b,e):
x,y,z = b
X,Y,Z = e
return (X-x, Y-y, Z-z)
def unit(v):
x,y,z = v
mag = length(v)
return (x/mag, y/mag, z/mag)
def distance(p0,p1):
return length(vector(p0,p1))
def scale(v,sc):
x,y,z = v
return (x * sc, y * sc, z * sc)
def add(v,w):
x,y,z = v
X,Y,Z = w
return (x+X, y+Y, z+Z)
# Given a line with coordinates 'start' and 'end' and the
# coordinates of a point 'pnt' the proc returns the shortest
# distance from pnt to the line and the coordinates of the
# nearest point on the line.
#
# 1 Convert the line segment to a vector ('line_vec').
# 2 Create a vector connecting start to pnt ('pnt_vec').
# 3 Find the length of the line vector ('line_len').
# 4 Convert line_vec to a unit vector ('line_unitvec').
# 5 Scale pnt_vec by line_len ('pnt_vec_scaled').
# 6 Get the dot product of line_unitvec and pnt_vec_scaled ('t').
# 7 Ensure t is in the range 0 to 1.
# 8 Use t to get the nearest location on the line to the end
# of vector pnt_vec_scaled ('nearest').
# 9 Calculate the distance from nearest to pnt_vec_scaled.
# 10 Translate nearest back to the start/end line.
# Malcolm Kesson 16 Dec 2012
def pnt2line(pnt, start, end):
line_vec = vector(start, end)
pnt_vec = vector(start, pnt)
line_len = length(line_vec)
line_unitvec = unit(line_vec)
pnt_vec_scaled = scale(pnt_vec, 1.0/line_len)
t = dot(line_unitvec, pnt_vec_scaled)
if t < 0.0:
t = 0.0
elif t > 1.0:
t = 1.0
nearest = scale(line_vec, t)
dist = distance(nearest, pnt_vec)
nearest = add(nearest, start)
return (dist, nearest)
Вместо использования цикла for вы можете векторизовать эти операции и добиться гораздо большей производительности. Вот мое решение, которое позволяет вычислить расстояние от одной точки до нескольких сегментов линии с помощью векторизованных вычислений.
def lineseg_dists(p, a, b):
"""Cartesian distance from point to line segment
Edited to support arguments as series, from:
https://stackru.com/a/54442561/11208892
Args:
- p: np.array of single point, shape (2,) or 2D array, shape (x, 2)
- a: np.array of shape (x, 2)
- b: np.array of shape (x, 2)
"""
# normalized tangent vectors
d_ba = b - a
d = np.divide(d_ba, (np.hypot(d_ba[:, 0], d_ba[:, 1])
.reshape(-1, 1)))
# signed parallel distance components
# rowwise dot products of 2D vectors
s = np.multiply(a - p, d).sum(axis=1)
t = np.multiply(p - b, d).sum(axis=1)
# clamped parallel distance
h = np.maximum.reduce([s, t, np.zeros(len(s))])
# perpendicular distance component
# rowwise cross products of 2D vectors
d_pa = p - a
c = d_pa[:, 0] * d[:, 1] - d_pa[:, 1] * d[:, 0]
return np.hypot(h, c)
И несколько тестов:
p = np.array([0, 0])
a = np.array([[ 1, 1],
[-1, 0],
[-1, -1]])
b = np.array([[ 2, 2],
[ 1, 0],
[ 1, -1]])
print(lineseg_dists(p, a, b))
p = np.array([[0, 0],
[1, 1],
[0, 2]])
print(lineseg_dists(p, a, b))
>>> [1.41421356 0. 1. ]
[1.41421356 1. 3. ]
Объяснение в документации этой функции:
def point_to_line_dist(point, line):
"""Calculate the distance between a point and a line segment.
To calculate the closest distance to a line segment, we first need to check
if the point projects onto the line segment. If it does, then we calculate
the orthogonal distance from the point to the line.
If the point does not project to the line segment, we calculate the
distance to both endpoints and take the shortest distance.
:param point: Numpy array of form [x,y], describing the point.
:type point: numpy.core.multiarray.ndarray
:param line: list of endpoint arrays of form [P1, P2]
:type line: list of numpy.core.multiarray.ndarray
:return: The minimum distance to a point.
:rtype: float
"""
# unit vector
unit_line = line[1] - line[0]
norm_unit_line = unit_line / np.linalg.norm(unit_line)
# compute the perpendicular distance to the theoretical infinite line
segment_dist = (
np.linalg.norm(np.cross(line[1] - line[0], line[0] - point)) /
np.linalg.norm(unit_line)
)
diff = (
(norm_unit_line[0] * (point[0] - line[0][0])) +
(norm_unit_line[1] * (point[1] - line[0][1]))
)
x_seg = (norm_unit_line[0] * diff) + line[0][0]
y_seg = (norm_unit_line[1] * diff) + line[0][1]
endpoint_dist = min(
np.linalg.norm(line[0] - point),
np.linalg.norm(line[1] - point)
)
# decide if the intersection point falls on the line segment
lp1_x = line[0][0] # line point 1 x
lp1_y = line[0][1] # line point 1 y
lp2_x = line[1][0] # line point 2 x
lp2_y = line[1][1] # line point 2 y
is_betw_x = lp1_x <= x_seg <= lp2_x or lp2_x <= x_seg <= lp1_x
is_betw_y = lp1_y <= y_seg <= lp2_y or lp2_y <= y_seg <= lp1_y
if is_betw_x and is_betw_y:
return segment_dist
else:
# if not, then return the minimum distance to the segment endpoints
return endpoint_dist
Основной алгоритм: представьте, что у вас есть линии, настолько ориентированные, что A лежит слева от B,
Найти ближайшую точку, как обычно. Если точка находится между A а также BГотово. Если это слева от Aближайшая точка A, Если точка находится справа от Bближайшая точка B,
Случай, когда A, B, а также O все лежат на одной линии, может или не может нуждаться в особом внимании. Обязательно включите несколько тестов этой позиции.
Со своей стороны, я обнаружил, что два других ответа были разбиты, особенно когда линия чисто вертикальная или горизонтальная. Вот что я сделал, чтобы правильно решить проблему.
Код Python:
def sq_shortest_dist_to_point(self, other_point):
dx = self.b.x - self.a.x
dy = self.b.y - self.a.y
dr2 = float(dx ** 2 + dy ** 2)
lerp = ((other_point.x - self.a.x) * dx + (other_point.y - self.a.y) * dy) / dr2
if lerp < 0:
lerp = 0
elif lerp > 1:
lerp = 1
x = lerp * dx + self.a.x
y = lerp * dy + self.a.y
_dx = x - other_point.x
_dy = y - other_point.y
square_dist = _dx ** 2 + _dy ** 2
return square_dist
def shortest_dist_to_point(self, other_point):
return math.sqrt(self.sq_shortest_dist_to_point(other_point))
Тестовый пример:
def test_distance_to_other_point(self):
# Parametrize test with multiple cases:
segments_and_point_and_answer = [
[Segment(Point(1.0, 1.0), Point(1.0, 3.0)), Point(2.0, 4.0), math.sqrt(2.0)],
[Segment(Point(1.0, 1.0), Point(1.0, 3.0)), Point(2.0, 3.0), 1.0],
[Segment(Point(0.0, 0.0), Point(0.0, 3.0)), Point(1.0, 1.0), 1.0],
[Segment(Point(1.0, 1.0), Point(3.0, 3.0)), Point(2.0, 2.0), 0.0],
[Segment(Point(-1.0, -1.0), Point(3.0, 3.0)), Point(2.0, 2.0), 0.0],
[Segment(Point(1.0, 1.0), Point(1.0, 3.0)), Point(2.0, 3.0), 1.0],
[Segment(Point(1.0, 1.0), Point(1.0, 3.0)), Point(2.0, 4.0), math.sqrt(2.0)],
[Segment(Point(1.0, 1.0), Point(-3.0, -3.0)), Point(-3.0, -4.0), 1],
[Segment(Point(1.0, 1.0), Point(-3.0, -3.0)), Point(-4.0, -3.0), 1],
[Segment(Point(1.0, 1.0), Point(-3.0, -3.0)), Point(1, 2), 1],
[Segment(Point(1.0, 1.0), Point(-3.0, -3.0)), Point(2, 1), 1],
[Segment(Point(1.0, 1.0), Point(-3.0, -3.0)), Point(-3, -1), math.sqrt(2.0)],
[Segment(Point(1.0, 1.0), Point(-3.0, -3.0)), Point(-1, -3), math.sqrt(2.0)],
[Segment(Point(-1.0, -1.0), Point(3.0, 3.0)), Point(3, 1), math.sqrt(2.0)],
[Segment(Point(-1.0, -1.0), Point(3.0, 3.0)), Point(1, 3), math.sqrt(2.0)],
[Segment(Point(1.0, 1.0), Point(3.0, 3.0)), Point(3, 1), math.sqrt(2.0)],
[Segment(Point(1.0, 1.0), Point(3.0, 3.0)), Point(1, 3), math.sqrt(2.0)]
]
for i, (segment, point, answer) in enumerate(segments_and_point_and_answer):
result = segment.shortest_dist_to_point(point)
self.assertAlmostEqual(result, answer, delta=0.001, msg=str((i, segment, point, answer)))
Примечание: я предполагаю, что эта функция находится внутри Segment учебный класс. Если ваша линия бесконечна, не ограничивайте lerp только от 0 до 1, но все же, по крайней мере, дают два различных a а также b точки.
Я также должен был решить эту проблему, поэтому ради доступности я опубликую свой код здесь. Я сделал небольшую проверку, но ничего особенно серьезного. Ваш вопрос фактически помог мне определить ошибку в моем, когда сегмент вертикальной или горизонтальной линии нарушил бы код и обошел точку пересечения в логике сегмента.
from math import sqrt
def dist_to_segment(ax, ay, bx, by, cx, cy):
"""
Computes the minimum distance between a point (cx, cy) and a line segment with endpoints (ax, ay) and (bx, by).
:param ax: endpoint 1, x-coordinate
:param ay: endpoint 1, y-coordinate
:param bx: endpoint 2, x-coordinate
:param by: endpoint 2, y-coordinate
:param cx: point, x-coordinate
:param cy: point, x-coordinate
:return: minimum distance between point and line segment
"""
# avoid divide by zero error
a = max(by - ay, 0.00001)
b = max(ax - bx, 0.00001)
# compute the perpendicular distance to the theoretical infinite line
dl = abs(a * cx + b * cy - b * ay - a * ax) / sqrt(a**2 + b**2)
# compute the intersection point
x = ((a / b) * ax + ay + (b / a) * cx - cy) / ((b / a) + (a / b))
y = -1 * (a / b) * (x - ax) + ay
# decide if the intersection point falls on the line segment
if (ax <= x <= bx or bx <= x <= ax) and (ay <= y <= by or by <= y <= ay):
return dl
else:
# if it does not, then return the minimum distance to the segment endpoints
return min(sqrt((ax - cx)**2 + (ay - cy)**2), sqrt((bx - cx)**2 + (by - cy)**2))