Построение амплитудных и фазовых спектров wav-файла в диапазоне от -fs/2 до fs / 2
У меня проблемы с отображением БПФ файла WAV. Мне удалось построить амплитудные и фазовые спектры сигнала, однако мне нужно повторить это в диапазоне -fs/2:fs/2,
%read sound files
%'y' is the vector holding the original samples & 'fs' refers to the sampling frequency
[y,fs] = wavread('handel.wav');
ydft = fft(y); %fft to transform the original signal into frequency domain
n = length (y); %length of the original signal
% y has even length
ydft = ydft(1:length(y)/2+1);
% create a frequency vector
freq = 0:fs/length(y):fs/2;
shiftfreq = fftshift(freq);
%plot original signal in time domain;
figure;
plot ((1:n)/fs, y);
title('handel.wav in time domain');
xlabel ('second');
grid on;
% plot magnitude in frequency domain
figure;
plot(freq,abs(ydft));
title('handel.wav in frequency domain');
xlabel ('Hz');
ylabel('Magnitude');
grid on;
% plot phase in frequency domain
figure;
plot(freq,unwrap(angle(ydft)));
title ('handel.wav in frequency domain');
xlabel ('Hz');
ylabel ('Phase');
grid on;
3 ответа
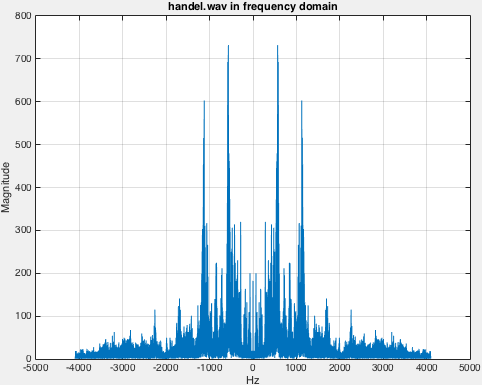
То, что вы сейчас делаете, - это построение полуспектрала, поэтому 0 <= f < fs/2 где fs частота дискретизации вашего сигнала, и так fs/2 частота Найквиста Обратите внимание, что учет половины спектра действителен только в том случае, если сигнал реальный. Это означает, что отрицательные спектры симметричны положительным спектрам, и поэтому вам не нужно рассматривать отрицательные спектры здесь.
Тем не менее, вы хотели бы построить полный спектр величины и фазы. Обратите внимание, что при расчете fft используя MATLAB, он использует алгоритм Кули-Тьюки, поэтому при вычислении N точка FFT, половина результата для частот от 0 Гц включительно до fs/2 Гц эксклюзив, а другая половина для частот от -fs/2 Гц включительно до 0 Гц эксклюзив.
Таким образом, чтобы построить полный спектр, просто выполните fftshift на полном сигнале так, чтобы правая половина и левая половина спектра менялись местами так, чтобы частота 0 Гц находилась в центре сигнала. Кроме того, вы должны генерировать частоты между -fs/2 в fs/2 чтобы охватить весь спектр. В частности, вам нужно сгенерировать N точки, линейно расположенные между -fs/2 в fs/2, Тем не менее, обратите внимание, что частота Найквиста в fs/2 Гц исключается в конце, поэтому вам нужно сгенерировать N+1 точки между -fs/2 в fs/2 и удалите последнюю точку, чтобы правильный размер шага между каждым частотным интервалом был правильным. Самый простой способ создать этот линейный массив точек - использовать linspace команда, где начальная частота -fs/2 конечная частота fs/2 и вы хотите N+1 точки между этим диапазоном и удалить последнюю точку:
freq = linspace(-fs/2, fs/2, n+1);
freq(end) = [];
Таким образом, заимствуя некоторые части вашего кода, вот как выглядит модифицированный код для построения полного спектра величины и фазы:
%// Read in sound file
[y,fs] = wavread('handel.wav');
%// Take N-point FFT where N is the length of the signal
ydft = fft(y);
n = numel(y); %// Get N - length of signal
%// Create frequency vector - make sure you remove last point
freq = linspace(-fs/2, fs/2, n+1);
freq(end) = [];
%// Shift the spectrum
shiftSpectrum = fftshift(ydft);
%//plot original signal in time domain;
figure;
plot ((0:n-1)/fs, y); %// Note you should start from time = 0, not time = 1/fs
title('handel.wav in time domain');
xlabel ('second');
grid on;
%// plot magnitude in frequency domain
figure;
plot(freq,abs(shiftSpectrum));
title('handel.wav in frequency domain');
xlabel ('Hz');
ylabel('Magnitude');
grid on;
%// plot phase in frequency domain
figure;
plot(freq,unwrap(angle(shiftSpectrum)));
title('handel.wav in frequency domain');
xlabel('Hz');
ylabel('Phase');
grid on;
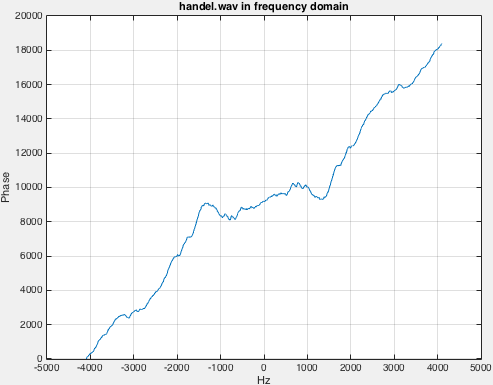
У меня нет доступа к вашему handel.wav файл, но я буду использовать тот, который поставляется с MATLAB. Вы можете загрузить это с load handel;, Частота дискретизации сохраняется в переменной под названием Fs так что мне пришлось сделать fs = Fs; прежде чем код, который я написал выше, может работать. Частота дискретизации для этого конкретного файла составляет 8192 Гц, и это приблизительно 9-секундный файл (numel(y) / fs = 8.9249 секунд). С этим файлом, это величина и фаза, которую я получаю:
Для дискретного преобразования Фурье (DFT), а также его быстрых реализаций (FFT) частоты нормализуются с частотой дискретизации fs, т. Е. Исходный диапазон -fs/2:fs/2 изменяется на -pi:pi.
Кроме того, DFT/FFT всегда начинается с 0, и вы можете использовать fftshift() для смещения частоты 0 к центру. Поэтому после fftshift() диапазон равен -pi:pi, тогда вы можете масштабировать до -fs/2:fs/2.
Посмотрите на следующую функцию Matlab, она может рассчитать фазовый спектр, а также амплитудный спектр с идеальной точностью:
Эта программа рассчитывает амплитудные и фазовые спектры входного сигнала с приемлемой точностью, особенно при расчете фазового спектра. Код выполняет три основных задания для расчета амплитудных и фазовых спектров. Прежде всего, он расширяет входной сигнал до бесконечности; Поскольку для вычисления преобразования Фурье (FT) (функция fft в Matlab) мы считаем, что наш сигнал является периодическим с бесконечной длиной волны, код создает super_signal, помещая исходный сигнал рядом с собой до тех пор, пока длина super_signal не составит около 1000000 отсчетов, почему Я выбираю 1000000 образцов? На самом деле, это просто на основе проб и ошибок! Для большинства сигналов, которые я пробовал, наилучшим выходом является сигнал ужина с 1000000 выборками.
Во-вторых, для вычисления fft в Matlab вы можете выбрать разные разрешения, документ Mathwork и помочь использовать NFFT=2^nextpow2(длина (сигнал)), этого явно недостаточно для того, кто хочет получить высокую точность вывода. Здесь я выбираю разрешение NFFT=100000, которое подходит для большинства сигналов.
В-третьих, код фильтрует результат FT с помощью порогового значения, это очень важный шаг! Для расчета фазового спектра, его результат очень шумный из-за плавающей ошибки округления, он вызывает во время вычисления "arctan", даже небольшая ошибка округления производит значительный шум в результате фазового спектра, для подавления этого вида шума вы можете определить порог значение. Это означает, что если амплитуда определенной частоты меньше, чем предопределенное пороговое значение (вы должны определить его), то вместо нуля ставится ноль.
Эти три шага помогают значительно улучшить результат амплитудных и фазовых спектров.
ЕСЛИ ВЫ ИСПОЛЬЗУЕТЕ ЭТУ ПРОГРАММУ В ИССЛЕДОВАНИИ, ПОЖАЛУЙСТА, СМОТРИТЕ СЛЕДУЮЩУЮ БУМАГУ:
Афшин Агаян, Приянк Джайсвал и Хамид Реза Сиакухи (2016). "Сейсмическое шумоподавление с использованием избыточной схемы подъема". ГЕОФИЗИКА, 81 (3), V249-V260. https://doi.org/10.1190/geo2015-0601.1