Создание труб с некруглыми сечениями в MuPad

Question

С помощью plot::tube Функция в MuPAD, я могу создавать трубы с изменяющимся позвоночником, но поперечное сечение всегда является кругом, хотя радиус может варьироваться вдоль позвоночника. Например:

plot::Tube([cos(t), sin(t), 0], 0.4 + 0.3*sin(t)*cos(t),t = -0.5*PI..0.5*PI,Mesh=[60,12]):

Я хочу построить трубы с (некруглыми) эллиптическими сечениями. Есть ли способ добиться этого в MuPAD?

PS Я могу генерировать трубы с произвольным поперечным сечением, используя MATLAV, поэтому, пожалуйста, избегайте ответов, которые используют чистые команды MATLAB.

Answer 1

Что касается вашего первого вопроса, можно ли это сделать с plot::TubeЯ так не думаю. Рассмотрим помощь этой функции (выделение мое):

plot::Tube создает обобщенные трубчатые графики, известные как "поверхности каналов", с особыми случаями, известными как "поверхность труб", "поверхность труб" или "трубчатые поверхности".

Интуитивно понятно, что поверхности каналов представляют собой пространственные кривые с толщиной. Более формально, поверхность канала plot::Tube([x(t), y(t), z(t)], r(t), t = t_min..t_max) это оболочка сфер с центром [x(t), y(t), z(t)] и радиус r(t)толщина кривой может меняться в зависимости от параметра кривой t

Тот факт, что труба определяется как оболочка набора сфер, предполагает, что их поперечное сечение по своей природе является круглым.

Я не знаком с MuPAD, поэтому я не знаю элегантного решения вашей проблемы. Для вашего простого примера полукруглой базовой линии я мог бы собрать это грязное решение, используя низкий уровень plot::Surface, вручную строим поверхность:

plot(
  plot::Surface(
      matrix([cos(t),sin(t),0]) 
      + numeric::rotationMatrix(t,[0,0,1]) * matrix([(0.2+0.1*sin(2*t))*cos(u),0,(0.2+0.1*cos(2*t))*sin(u)]),
      t = -PI/2..PI/2,
      u = 0..2*PI,
      Mesh = [30,30]),
  Scaling=Constrained)

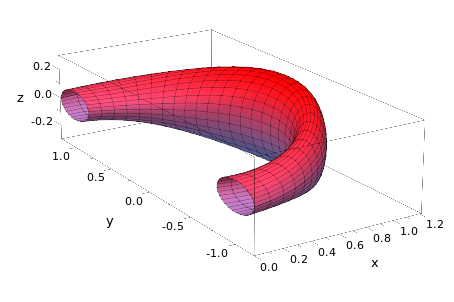
Вот t обозначает угловой параметр вдоль полукруглой базовой линии (тороидальное направление), и u угол вдоль поперечного сечения (полоидальное направление). Данное сечение под углом t выглядит так:

[(0.2+0.1*sin(2*t))*cos(u), 0, (0.2+0.1*cos(2*t))*sin(u)]

Т.е. большие полуоси (0.2+0.1*sin(2*t)) а также (0.2+0.1*cos(2*t)) вдоль поперечного сечения трубки.

Вы можете видеть, что я использовал матрицу вращения вокруг z ось для построения поверхности. Это в значительной степени использовало тот факт, что базовая линия представляет собой полукруг. Однако в общих случаях должна быть возможность вычислить производную вашей параметризованной базовой линии (по отношению к t) и рассчитать необходимый угол поворота (с параметром t) От этого.