glmmTMB в R бета-регрессии или пуассоновском распределении?
У меня есть набор данных, который очень ноль раздут. Нули являются репрезентативными для истинных нулей. Это означает, что в этом случае ноль - это допустимое значение, указывающее что-либо о тестируемых лицах (мера уязвимости к чему-либо) - 0 = низкая уязвимость.
Я моделирую, используя glmm с нулевой инфляцией от glmmTMB с отдельным в качестве случайного компонента модели.
Однако я не уверен, стоит ли использовать бета-распределение с нулевой инфляцией и использовать преобразования, чтобы позаботиться о 0 значениях, поскольку я читал, что бета-распределение обрабатывает что-то между 0 и 1, но не 0/1 (это преобразование: ответ. вар *(п-1)+0,5)/ п). Это добавило бы небольшое количество к нулям, делая их подходящими.
ИЛИ ЖЕ
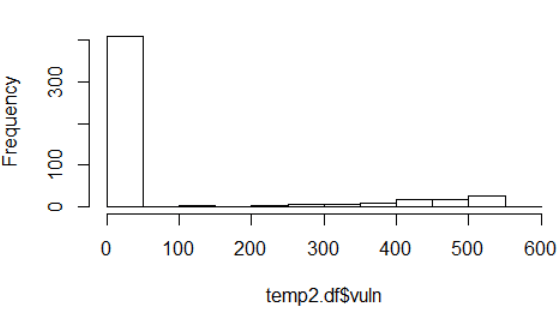
Использовать альтернативный подход, то есть модель Пуассона с 0 завышенными значениями. Ниже приведено распределение переменной отклика (я должен упомянуть, что этот нетрансформированный ограничен между 0 и 600 или как пропорция между 0 и 1)
Может кто-нибудь посоветовать, какой из этих двух вариантов является наиболее подходящим или неправильным? Благодарю.
PS Я указал бета-дистрибутив как это в выноске:
family=list(family="beta",link="logit")
Это правильно?