Построить DFA языка L = { L1 \ L2 }
Как я могу построить DFA языка L = { L1 \ L2 }
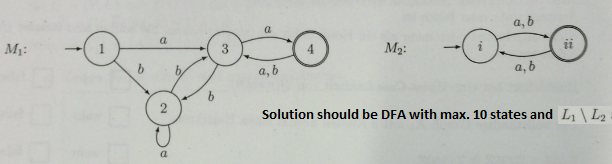
DFA для L1 и L2 даны, но как я могу "вычесть" один DFA из другого? Возможно ли это как-то с относительным дополнением http://en.wikipedia.org/wiki/Complement_(set_theory) и законом DeMorgans?
Мое решение: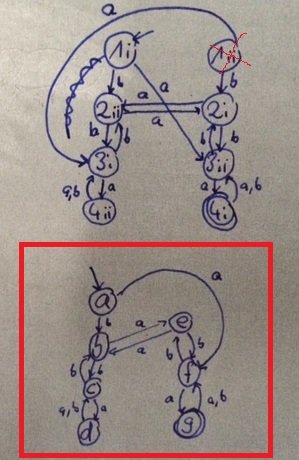
1 ответ
Насколько я понимаю, желаемый DFA может быть получен с помощью модифицированного автомата продукта, который используется для пересечения L1 а также L2, но состояния терминала должны быть определены по-разному. Вместо того, чтобы делать состояние продукта (q_1,q_2) состояние терминала, если и только если q_1 а также q_2 являются терминальными состояниями в A(L1) а также A(L2) соответственно, определите его как состояние терминала, если и только если q_1 это состояние терминала и q_2 это не состояние терминала.
Я не совсем уверен, что, если не считать этого элементарного аргумента, результат может быть применен при заданной формулировке закона де Моргана.