Решить уравнение теплопроводности с ненулевыми БК Дирихле с неявным линейным решателем Эйлера и сопряженного градиента?

Question

Многие пользователи спрашивают, как решить уравнение теплопроводности, u_t = u_xx, с ненулевыми BC Дирихле и с сопряженными градиентами для внутреннего линейного решателя. Это общая упрощенная проблема PDE перед переходом к более сложным версиям параболических PDE. Как это сделать в DifferentialEquations.jl?

Answer 1

Давайте решать эту проблему поэтапно. Во-первых, давайте построим линейный оператор для дискретного уравнения теплопроводности с БК Дирихле. Обсуждение дискретизации можно найти на этой вики-странице, которая показывает, что метод центральной разности дает дискретизацию второго порядка второй производной по (u[i-1] - 2u[i] + u[i+1])/dx^2, Это то же самое, что умножение на трехдиагональную матрицу [1 -2 1]*(1/dx^2) Итак, начнем с построения этой матрицы:

using LinearAlgebra, OrdinaryDiffEq
x = collect(-π : 2π/511 : π)

## Dirichlet 0 BCs

u0 = @. -(x).^2 + π^2

n = length(x)
A = 1/(2π/511)^2 * Tridiagonal(ones(n-1),-2ones(n),ones(n-1))

Обратите внимание, что мы неявно упростили конец, так как (u[0] - 2u[1] + u[2])/dx^2 = (- 2u[1] + u[2])/dx^2 когда левый БК равен нулю, то термин удаляется из матмуля. Затем мы используем эту дискретизацию производной для решения уравнения теплопроводности:

function f(du,u,A,t)
    mul!(du,A,u)
end

prob = ODEProblem(f,u0,(0.0,10.0),A)
sol = solve(prob,ImplicitEuler())

using Plots
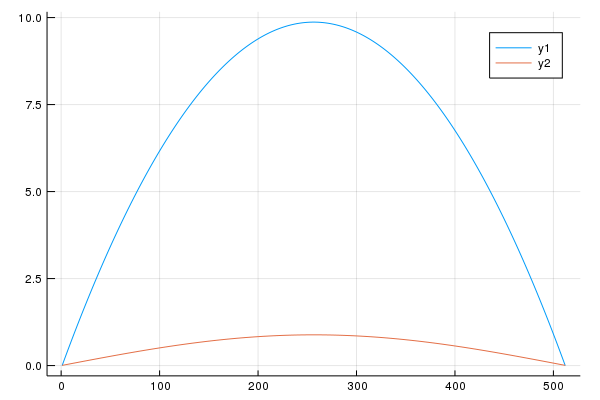
plot(sol[1])
plot!(sol[end])

Теперь мы делаем БК ненулевыми. Обратите внимание, что мы просто должны добавить обратно u[0]/dx^2 что мы ранее высадили, поэтому имеем:

## Dirichlet non-zero BCs
## Note that the operator is no longer linear
## To handle affine BCs, we add the dropped term

u0 = @. (x - 0.5).^2 + 1/12
n = length(x)
A = 1/(2π/511)^2 * Tridiagonal(ones(n-1),-2ones(n),ones(n-1))

function f(du,u,A,t)
    mul!(du,A,u)
    # Now do the affine part of the BCs
    du[1] += 1/(2π/511)^2 * u0[1]
    du[end] += 1/(2π/511)^2 * u0[end]
end

prob = ODEProblem(f,u0,(0.0,10.0),A)
sol = solve(prob,ImplicitEuler())

plot(sol[1])
plot!(sol[end])

Теперь давайте поменяем линейный решатель. В документации говорится, что вы просто даете Val{:init} dispatch, который возвращает тип для использования в качестве линейного решателя, поэтому мы делаем:

## Create a linear solver for GMRES
using IterativeSolvers

function linsolve!(::Type{Val{:init}},f,u0)
  function _linsolve!(x,A,b,update_matrix=false)
    cg!(x,A,b)
  end
end

sol = solve(prob,ImplicitEuler(linsolve=linsolve!))

plot(sol[1])
plot!(sol[end])

И вот, мы имеем ненулевое уравнение Тепла Дирихле с методом Крылова (сопряженные градиенты) для линейного решателя, что делает его методом Ньютона-Крылова.