График с двумя осями y, одной осью y слева и другой осью y справа
Мне нужно построить гистограмму, показывающую количество и линейную диаграмму, показывающую скорость на одном графике, я могу сделать их оба отдельно, но когда я их соединю, я масштабирую первый слой (т.е. geom_bar) перекрывается вторым слоем (т.е. geom_line).
Могу ли я переместить ось geom_line направо?
18 ответов
Иногда клиент хочет два y весов. Давать им "некорректную" речь часто бессмысленно. Но мне нравится, что ggplot2 настойчиво делает все правильно. Я уверен, что ggplot на самом деле обучает обычного пользователя правильной технике визуализации.
Может быть, вы можете использовать гранение и масштабирование бесплатно, чтобы сравнить два ряда данных? - например, посмотрите здесь: https://github.com/hadley/ggplot2/wiki/Align-two-plots-on-a-page
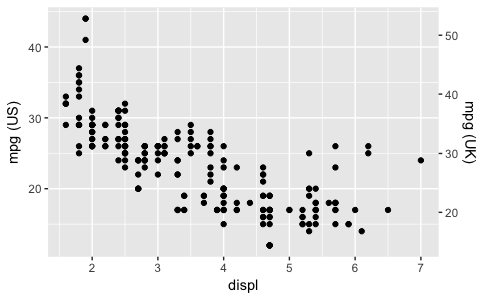
Начиная с ggplot2 2.2.0, вы можете добавить дополнительную ось, подобную этой (взято из объявления ggplot2 2.2.0):
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
scale_y_continuous(
"mpg (US)",
sec.axis = sec_axis(~ . * 1.20, name = "mpg (UK)")
)Это невозможно в ggplot2, потому что я считаю, что графики с отдельными y-масштабами (не y-масштабами, которые являются преобразованиями друг друга) в корне ошибочны. Некоторые проблемы:
Не являются обратимыми: учитывая точку на пространстве графика, вы не можете однозначно сопоставить ее с точкой в пространстве данных.
Их относительно трудно правильно прочитать по сравнению с другими вариантами. Подробности см. В исследовании диаграмм данных двойного масштаба, проведенном Петрой Изенберг, Анастасией Безерианос, Пьером Драгичевичем и Жаном-Даниэлем Фекете.
Их легко манипулировать, чтобы ввести в заблуждение: не существует уникального способа указать относительные масштабы осей, оставляя их открытыми для манипуляций. Два примера из блога Junkcharts: один, два
Они произвольны: почему только 2 шкалы, а не 3, 4 или десять?
Вы также можете прочитать подробное обсуждение Стивена Фью на тему " Двухмасштабные оси в графах". Являются ли они когда-либо лучшим решением?,
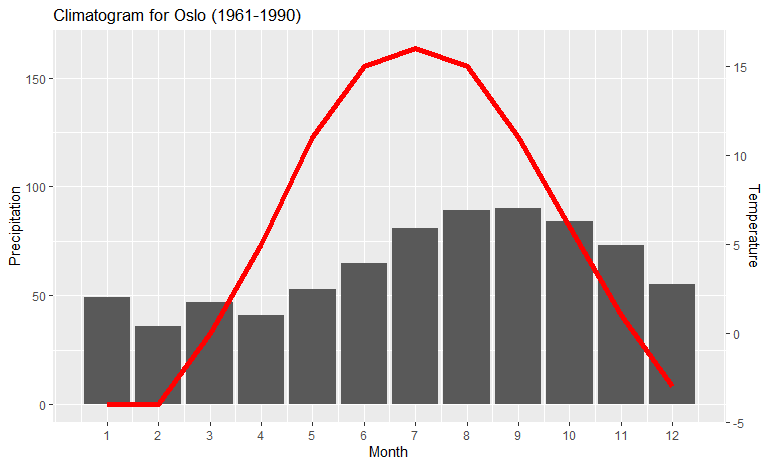
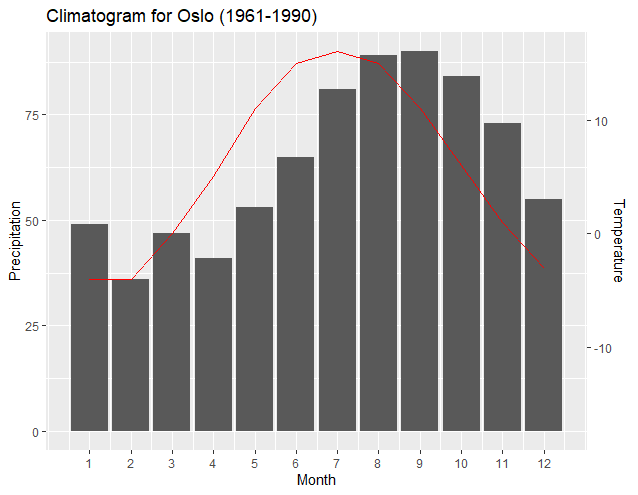
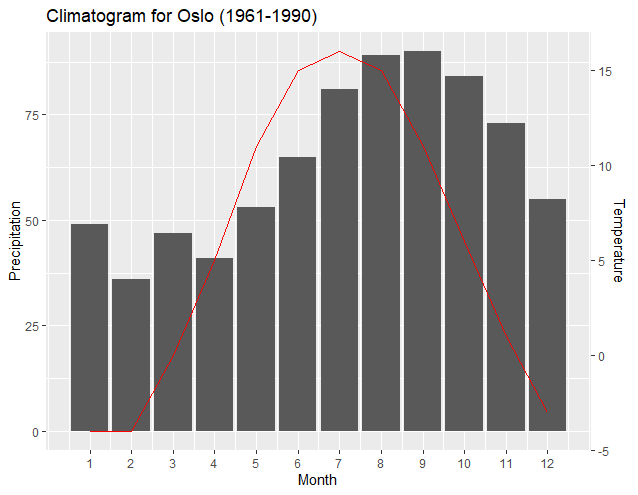
Существуют общие случаи использования дуэльных осей, например, климатограф, показывающий месячную температуру и количество осадков. Вот простое решение, обобщенное на основе решения Мегатрона, позволяющее вам установить нижний предел переменных на значение, отличное от нуля:
Пример данных:
climate <- tibble(
Month = 1:12,
Temp = c(-4,-4,0,5,11,15,16,15,11,6,1,-3),
Precip = c(49,36,47,41,53,65,81,89,90,84,73,55)
)
Установите пределы каждой оси вручную:
ylim.prim <- c(0, 180) # in this example, precipitation
ylim.sec <- c(-4, 18) # in this example, temperature
Следующее делает необходимые вычисления, основанные на этих пределах, и делает сам график:
b <- diff(ylim.prim)/diff(ylim.sec)
a <- b*(ylim.prim[1] - ylim.sec[1])
ggplot(climate, aes(Month, Precip)) +
geom_col() +
geom_line(aes(y = a + Temp*b), color = "red") +
scale_y_continuous("Precipitation", sec.axis = sec_axis(~ (. - a)/b, name = "Temperature")) +
scale_x_continuous("Month", breaks = 1:12) +
ggtitle("Climatogram for Oslo (1961-1990)")
Если вы хотите убедиться, что красная линия соответствует правой оси Y, вы можете добавить theme предложение к коду:
ggplot(climate, aes(Month, Precip)) +
geom_col() +
geom_line(aes(y = a + Temp*b), color = "red") +
scale_y_continuous("Precipitation", sec.axis = sec_axis(~ (. - a)/b, name = "Temperature")) +
scale_x_continuous("Month", breaks = 1:12) +
theme(axis.line.y.right = element_line(color = "red"),
axis.ticks.y.right = element_line(color = "red"),
axis.text.y.right = element_text(color = "red"),
axis.title.y.right = element_text(color = "red")
) +
ggtitle("Climatogram for Oslo (1961-1990)")
который окрашивает правую ось:
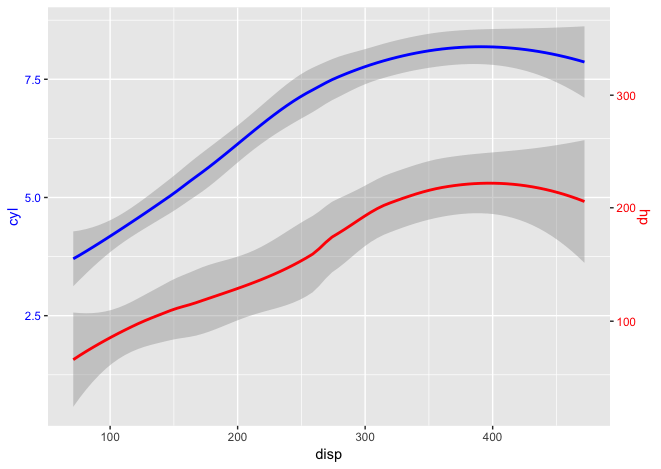
Вы можете создать коэффициент масштабирования, который применяется ко второму геому и правой оси Y. Это вытекает из решения Себастьяна.
library(ggplot2)
scaleFactor <- max(mtcars$cyl) / max(mtcars$hp)
ggplot(mtcars, aes(x=disp)) +
geom_smooth(aes(y=cyl), method="loess", col="blue") +
geom_smooth(aes(y=hp * scaleFactor), method="loess", col="red") +
scale_y_continuous(name="cyl", sec.axis=sec_axis(~./scaleFactor, name="hp")) +
theme(
axis.title.y.left=element_text(color="blue"),
axis.text.y.left=element_text(color="blue"),
axis.title.y.right=element_text(color="red"),
axis.text.y.right=element_text(color="red")
)
Примечание: использование ggplot2 v3.0.0
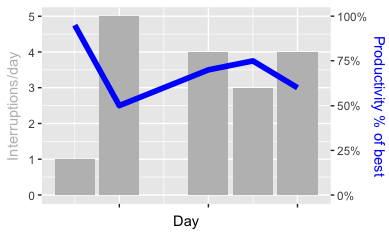
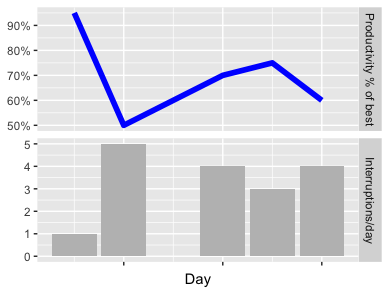
Принимая приведенные выше ответы и некоторые настройки (и чего бы это ни стоило), вот способ достижения двух шкал с помощью sec_axis:
Предположим, простой (и чисто вымышленный) набор данных dt: в течение пяти дней он отслеживает количество прерываний VS производительности:
when numinter prod
1 2018-03-20 1 0.95
2 2018-03-21 5 0.50
3 2018-03-23 4 0.70
4 2018-03-24 3 0.75
5 2018-03-25 4 0.60
(диапазоны обоих столбцов отличаются примерно в 5 раз).
Следующий код нарисует обе серии, что они используют всю ось Y:
ggplot() +
geom_bar(mapping = aes(x = dt$when, y = dt$numinter), stat = "identity", fill = "grey") +
geom_line(mapping = aes(x = dt$when, y = dt$prod*5), size = 2, color = "blue") +
scale_x_date(name = "Day", labels = NULL) +
scale_y_continuous(name = "Interruptions/day",
sec.axis = sec_axis(~./5, name = "Productivity % of best",
labels = function(b) { paste0(round(b * 100, 0), "%")})) +
theme(
axis.title.y = element_text(color = "grey"),
axis.title.y.right = element_text(color = "blue"))
Вот результат (код выше + подстройка цвета):
Дело (кроме использования sec_axis при указании y_scale необходимо умножить каждое значение 2-го ряда данных на 5 при указании ряда. Чтобы получить метки прямо в определении sec_axis, нужно затем разделить на 5 (и отформатировать). Таким образом, важная часть в приведенном выше коде действительно *5 в geom_line и ~./5 в sec_axis (формула, разделяющая текущее значение . на 5).
Для сравнения (я не хочу судить о подходах здесь), вот как выглядят две диаграммы друг над другом:
Вы сами можете судить, какой из них лучше переносить сообщение ("Не мешайте людям на работе!"). Думаю, это честный способ решить.
Полный код для обоих изображений (на самом деле это не больше, чем выше, просто завершен и готов к запуску) находится здесь: https://gist.github.com/sebastianrothbucher/de847063f32fdff02c83b75f59c36a7d более подробное объяснение здесь: https://sebastianrothbucher.github.io/datascience/r/visualization/ggplot/2018/03/24/two-scales-ggplot-r.html
Вот мои два цента на то, как сделать преобразования для вторичной оси. Во-первых, вы хотите связать диапазоны первичных и вторичных данных. Обычно это беспорядок с точки зрения загрязнения вашей глобальной среды переменными, которые вам не нужны.
Чтобы упростить эту задачу, мы создадим фабрику функций, которая производит две функции, причем
scales::rescale()делает всю тяжелую работу. Поскольку это замыкания, они осведомлены о среде, в которой они были созданы, поэтому у них есть «память» о
to а также
from параметры, сгенерированные перед созданием.
- Одна функция выполняет прямое преобразование: преобразует вторичные данные в первичный масштаб.
- Вторая функция выполняет обратное преобразование: преобразует данные из первичных единиц во вторичные единицы.
library(ggplot2)
library(scales)
# Function factory for secondary axis transforms
train_sec <- function(primary, secondary) {
from <- range(secondary)
to <- range(primary)
# Forward transform for the data
forward <- function(x) {
rescale(x, from = from, to = to)
}
# Reverse transform for the secondary axis
reverse <- function(x) {
rescale(x, from = to, to = from)
}
list(fwd = forward, rev = reverse)
}
Все это кажется довольно сложным, но создание фабрики функций упрощает все остальное. Теперь, прежде чем строить график, мы создадим соответствующие функции, показав фабрике первичные и вторичные данные. Мы будем использовать набор экономических данных, который имеет очень разные диапазоны для
unemploy а также
psavert столбцы.
sec <- with(economics, train_sec(unemploy, psavert))
Затем мы используем
y = sec$fwd(psavert) чтобы изменить масштаб вторичных данных на первичную ось, и укажите
~ sec$rev(.)в качестве аргумента преобразования вторичной оси. Это дает нам график, на котором первичный и вторичный диапазоны занимают одно и то же место на графике.
ggplot(economics, aes(date)) +
geom_line(aes(y = unemploy), colour = "blue") +
geom_line(aes(y = sec$fwd(psavert)), colour = "red") +
scale_y_continuous(sec.axis = sec_axis(~sec$rev(.), name = "psavert"))

Фабрика немного более гибкая, потому что если вы просто хотите изменить масштаб до максимума, вы можете передать данные, нижний предел которых равен 0.
# Rescaling the maximum
sec <- with(economics, train_sec(c(0, max(unemploy)),
c(0, max(psavert))))
ggplot(economics, aes(date)) +
geom_line(aes(y = unemploy), colour = "blue") +
geom_line(aes(y = sec$fwd(psavert)), colour = "red") +
scale_y_continuous(sec.axis = sec_axis(~sec$rev(.), name = "psavert"))

Создано 2021-02-05 пакетом REPEX (v0.3.0)
Я допускаю, что разница в этом примере не так очевидна, но если вы присмотритесь, вы увидите, что максимумы совпадают, а красная линия идет ниже синей.
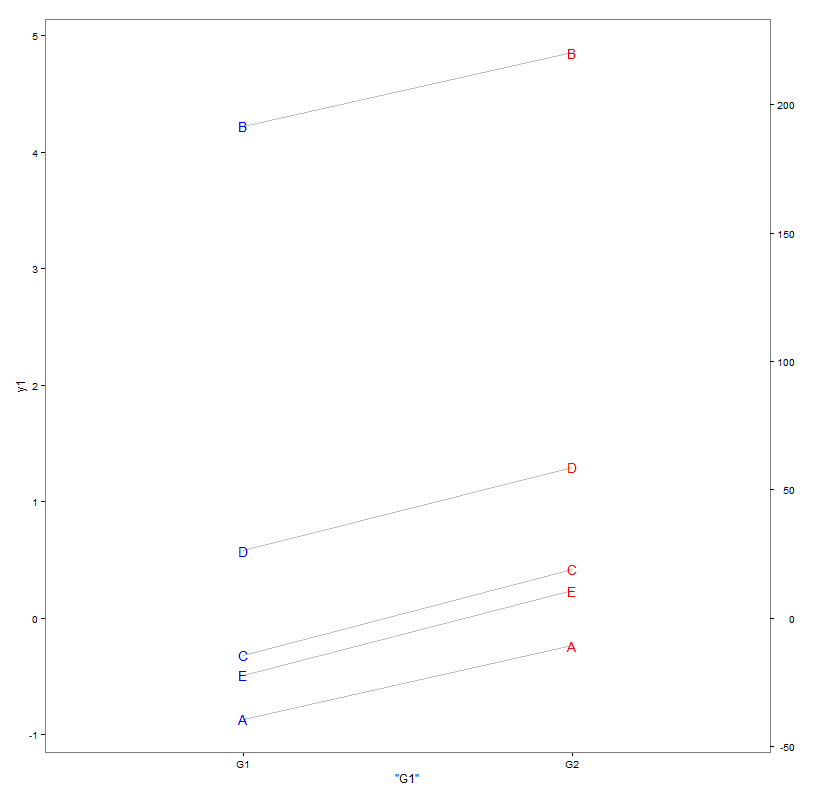
Техническая основа для решения этой проблемы была предоставлена Kohske около 3 лет назад [ KOHSKE ]. Тема и технические аспекты ее решения обсуждались в нескольких случаях здесь, на Stackru [ID: 18989001, 29235405, 21026598]. Поэтому я приведу только конкретный вариант и несколько поясняющих пошаговых инструкций, используя вышеуказанные решения.
Предположим, у нас есть некоторые данные y1 в группе G1, с которыми некоторые данные y2 в группе G2 связаны каким-либо образом, например, преобразованы диапазон / масштаб или добавлен некоторый шум. Таким образом, каждый хочет построить данные вместе на одном графике с масштабом y1 слева и y2 справа.
df <- data.frame(item=LETTERS[1:n], y1=c(-0.8684, 4.2242, -0.3181, 0.5797, -0.4875), y2=c(-5.719, 205.184, 4.781, 41.952, 9.911 )) # made up!
> df
item y1 y2
1 A -0.8684 -19.154567
2 B 4.2242 219.092499
3 C -0.3181 18.849686
4 D 0.5797 46.945161
5 E -0.4875 -4.721973
Если мы теперь нанесем наши данные вместе с чем-то вроде
ggplot(data=df, aes(label=item)) +
theme_bw() +
geom_segment(aes(x='G1', xend='G2', y=y1, yend=y2), color='grey')+
geom_text(aes(x='G1', y=y1), color='blue') +
geom_text(aes(x='G2', y=y2), color='red') +
theme(legend.position='none', panel.grid=element_blank())
это не выравнивается хорошо, поскольку меньший масштаб y1, очевидно, сворачивается большим масштабом y2.
Хитрость для решения этой проблемы состоит в том, чтобы технически построить оба набора данных по первой шкале y1, но сообщить вторую по вторичной оси с метками, показывающими исходную шкалу y2.
Поэтому мы создаем первую вспомогательную функцию CalcFudgeAxis, которая вычисляет и собирает элементы новой оси, которая будет показана. Функция может быть изменена в соответствии с предпочтениями ayones (эта просто отображает y2 в диапазон y1).
CalcFudgeAxis = function( y1, y2=y1) {
Cast2To1 = function(x) ((ylim1[2]-ylim1[1])/(ylim2[2]-ylim2[1])*x) # x gets mapped to range of ylim2
ylim1 <- c(min(y1),max(y1))
ylim2 <- c(min(y2),max(y2))
yf <- Cast2To1(y2)
labelsyf <- pretty(y2)
return(list(
yf=yf,
labels=labelsyf,
breaks=Cast2To1(labelsyf)
))
}
что дает немного:
> FudgeAxis <- CalcFudgeAxis( df$y1, df$y2 )
> FudgeAxis
$yf
[1] -0.4094344 4.6831656 0.4029175 1.0034664 -0.1009335
$labels
[1] -50 0 50 100 150 200 250
$breaks
[1] -1.068764 0.000000 1.068764 2.137529 3.206293 4.275058 5.343822
> cbind(df, FudgeAxis$yf)
item y1 y2 FudgeAxis$yf
1 A -0.8684 -19.154567 -0.4094344
2 B 4.2242 219.092499 4.6831656
3 C -0.3181 18.849686 0.4029175
4 D 0.5797 46.945161 1.0034664
5 E -0.4875 -4.721973 -0.1009335
Теперь я обернул решение Кохске во вторую вспомогательную функцию PlotWithFudgeAxis (в которую мы бросаем объект ggplot и вспомогательный объект новой оси):
library(gtable)
library(grid)
PlotWithFudgeAxis = function( plot1, FudgeAxis) {
# based on: https://rpubs.com/kohske/dual_axis_in_ggplot2
plot2 <- plot1 + with(FudgeAxis, scale_y_continuous( breaks=breaks, labels=labels))
#extract gtable
g1<-ggplot_gtable(ggplot_build(plot1))
g2<-ggplot_gtable(ggplot_build(plot2))
#overlap the panel of the 2nd plot on that of the 1st plot
pp<-c(subset(g1$layout, name=="panel", se=t:r))
g<-gtable_add_grob(g1, g2$grobs[[which(g2$layout$name=="panel")]], pp$t, pp$l, pp$b,pp$l)
ia <- which(g2$layout$name == "axis-l")
ga <- g2$grobs[[ia]]
ax <- ga$children[[2]]
ax$widths <- rev(ax$widths)
ax$grobs <- rev(ax$grobs)
ax$grobs[[1]]$x <- ax$grobs[[1]]$x - unit(1, "npc") + unit(0.15, "cm")
g <- gtable_add_cols(g, g2$widths[g2$layout[ia, ]$l], length(g$widths) - 1)
g <- gtable_add_grob(g, ax, pp$t, length(g$widths) - 1, pp$b)
grid.draw(g)
}
Теперь все можно собрать воедино: код ниже показывает, как предлагаемое решение может быть использовано в повседневной среде. Вызов plot теперь больше не отображает исходные данные y2, кроме клонированной версии yf (хранящейся в предварительно рассчитанном вспомогательном объекте FudgeAxis), которая работает в масштабе y1. Затем исходный объект ggplot обрабатывается вспомогательной функцией Кохске PlotWithFudgeAxis, чтобы добавить вторую ось, сохраняющую масштабы y2. Это также сюжет манипулируемого сюжета.
FudgeAxis <- CalcFudgeAxis( df$y1, df$y2 )
tmpPlot <- ggplot(data=df, aes(label=item)) +
theme_bw() +
geom_segment(aes(x='G1', xend='G2', y=y1, yend=FudgeAxis$yf), color='grey')+
geom_text(aes(x='G1', y=y1), color='blue') +
geom_text(aes(x='G2', y=FudgeAxis$yf), color='red') +
theme(legend.position='none', panel.grid=element_blank())
PlotWithFudgeAxis(tmpPlot, FudgeAxis)
Теперь график строится по желанию с двумя осями, y1 слева и y2 справа
Вышеупомянутое решение, прямо скажем, ограниченный шаткий взлом. Так как он работает с ядром ggplot, он выдаст несколько предупреждений о том, что мы обмениваемся постфактум масштабами и т. Д. С ним нужно обращаться осторожно, и он может вызвать нежелательное поведение в другой настройке. Также может потребоваться возиться с вспомогательными функциями, чтобы получить макет по желанию. Размещение легенды - такая проблема (она будет помещена между панелью и новой осью; именно поэтому я ее и отбросил). Масштабирование / выравнивание оси 2 также немного сложное: приведенный выше код хорошо работает, когда обе шкалы содержат "0", в противном случае одна ось сдвигается. Так определенно с некоторыми возможностями улучшить...
Если вы хотите сохранить изображение, нужно перевести вызов в устройство "открыть / закрыть":
png(...)
PlotWithFudgeAxis(tmpPlot, FudgeAxis)
dev.off()
Следующая статья помогла мне объединить два графика, сгенерированных ggplot2 в одной строке:
Несколько графиков на одной странице (ggplot2) от Cookbook for R
А вот как может выглядеть код в этом случае:
p1 <-
ggplot() + aes(mns)+ geom_histogram(aes(y=..density..), binwidth=0.01, colour="black", fill="white") + geom_vline(aes(xintercept=mean(mns, na.rm=T)), color="red", linetype="dashed", size=1) + geom_density(alpha=.2)
p2 <-
ggplot() + aes(mns)+ geom_histogram( binwidth=0.01, colour="black", fill="white") + geom_vline(aes(xintercept=mean(mns, na.rm=T)), color="red", linetype="dashed", size=1)
multiplot(p1,p2,cols=2)
Для меня самой сложной задачей было выяснить функцию преобразования между двумя осями. Я использовал myCurveFit для этого.
> dput(combined_80_8192 %>% filter (time > 270, time < 280))
structure(list(run = c(268L, 268L, 268L, 268L, 268L, 268L, 268L,
268L, 268L, 268L, 263L, 263L, 263L, 263L, 263L, 263L, 263L, 263L,
263L, 263L, 269L, 269L, 269L, 269L, 269L, 269L, 269L, 269L, 269L,
269L, 261L, 261L, 261L, 261L, 261L, 261L, 261L, 261L, 261L, 261L,
267L, 267L, 267L, 267L, 267L, 267L, 267L, 267L, 267L, 267L, 265L,
265L, 265L, 265L, 265L, 265L, 265L, 265L, 265L, 265L, 266L, 266L,
266L, 266L, 266L, 266L, 266L, 266L, 266L, 266L, 262L, 262L, 262L,
262L, 262L, 262L, 262L, 262L, 262L, 262L, 264L, 264L, 264L, 264L,
264L, 264L, 264L, 264L, 264L, 264L, 260L, 260L, 260L, 260L, 260L,
260L, 260L, 260L, 260L, 260L), repetition = c(8L, 8L, 8L, 8L,
8L, 8L, 8L, 8L, 8L, 8L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 5L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L,
6L, 6L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 4L, 4L, 4L, 4L,
4L, 4L, 4L, 4L, 4L, 4L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L
), module = structure(c(1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L), .Label = "scenario.node[0].nicVLCTail.phyVLC", class = "factor"),
configname = structure(c(1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L), .Label = "Road-Vlc", class = "factor"), packetByteLength = c(8192L,
8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L,
8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L,
8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L,
8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L,
8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L,
8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L,
8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L,
8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L,
8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L,
8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L,
8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L, 8192L
), numVehicles = c(2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L
), dDistance = c(80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L,
80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L,
80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L,
80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L,
80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L,
80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L,
80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L,
80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L,
80L, 80L, 80L, 80L, 80L, 80L, 80L, 80L), time = c(270.166006903445,
271.173853699836, 272.175873251122, 273.177524313334, 274.182946177105,
275.188959464989, 276.189675339937, 277.198250244799, 278.204619457189,
279.212562800009, 270.164199199177, 271.168527215152, 272.173072994958,
273.179210429715, 274.184351047337, 275.18980754378, 276.194816792995,
277.198598277809, 278.202398083519, 279.210634593917, 270.210674322891,
271.212395107473, 272.218871923292, 273.219060500457, 274.220486359614,
275.22401452372, 276.229646658839, 277.231060448138, 278.240407241942,
279.2437126347, 270.283554249858, 271.293168593832, 272.298574288769,
273.304413221348, 274.306272082517, 275.309023049011, 276.317805897347,
277.324403550028, 278.332855848701, 279.334046374594, 270.118608539613,
271.127947700074, 272.133887145863, 273.135726000491, 274.135994529981,
275.136563912708, 276.140120735361, 277.144298344151, 278.146885137621,
279.147552358659, 270.206015567272, 271.214618077209, 272.216566814903,
273.225435592582, 274.234014573683, 275.242949179958, 276.248417809711,
277.248800670023, 278.249750333404, 279.252926560188, 270.217182684494,
271.218357511397, 272.224698488895, 273.231112784327, 274.238740508457,
275.242715184122, 276.249053562718, 277.250325509798, 278.258488063493,
279.261141590137, 270.282904173953, 271.284689544638, 272.294220723234,
273.299749415592, 274.30628880553, 275.312075103126, 276.31579134717,
277.321905523606, 278.326305136748, 279.333056502253, 270.258991527456,
271.260224091407, 272.270076810133, 273.27052037648, 274.274119348094,
275.280808254502, 276.286353887245, 277.287064312339, 278.294444793276,
279.296772014594, 270.333066283904, 271.33877455992, 272.345842319903,
273.350858180493, 274.353972278505, 275.360454510107, 276.365088896161,
277.369166956941, 278.372571708911, 279.38017503079), distanceToTx = c(80.255266401689,
80.156059067023, 79.98823695539, 79.826647129071, 79.76678667135,
79.788239825292, 79.734539327997, 79.74766421514, 79.801243848241,
79.765920888341, 80.255266401689, 80.15850240049, 79.98823695539,
79.826647129071, 79.76678667135, 79.788239825292, 79.735078924078,
79.74766421514, 79.801243848241, 79.764622734914, 80.251248121732,
80.146436869316, 79.984682320466, 79.82292012342, 79.761908518748,
79.796988776281, 79.736920997657, 79.745038376718, 79.802638836686,
79.770029970452, 80.243475525691, 80.127918207499, 79.978303140866,
79.816259117883, 79.749322030693, 79.809916018889, 79.744456560867,
79.738655068783, 79.788697533211, 79.784288359619, 80.260412958482,
80.168426829066, 79.992034911214, 79.830845773284, 79.7756751763,
79.778156038931, 79.732399593756, 79.752769548846, 79.799967731078,
79.757585110481, 80.251248121732, 80.146436869316, 79.984682320466,
79.822062073459, 79.75884601899, 79.801590491435, 79.738335109094,
79.74347007248, 79.803215965043, 79.771471198955, 80.250257298678,
80.146436869316, 79.983831684476, 79.822062073459, 79.75884601899,
79.801590491435, 79.738335109094, 79.74347007248, 79.803849157574,
79.771471198955, 80.243475525691, 80.130180105198, 79.978303140866,
79.816881283718, 79.749322030693, 79.80984572883, 79.744456560867,
79.738655068783, 79.790548644175, 79.784288359619, 80.246349000313,
80.137056554491, 79.980581246037, 79.818924707937, 79.753176142361,
79.808777040341, 79.741609845588, 79.740770913572, 79.796316397253,
79.777593733292, 80.238796415443, 80.119021911134, 79.974810568944,
79.814065350562, 79.743657315504, 79.810146783217, 79.749945098869,
79.737122584544, 79.781650522348, 79.791554933936), headerNoError = c(0.99999999989702,
0.9999999999981, 0.99999999999946, 0.9999999928026, 0.99999873265475,
0.77080141574964, 0.99007491438593, 0.99994396605059, 0.45588747062284,
0.93484381262491, 0.99999999989702, 0.99999999999816, 0.99999999999946,
0.9999999928026, 0.99999873265475, 0.77080141574964, 0.99008458785106,
0.99994396605059, 0.45588747062284, 0.93480223051707, 0.99999999989735,
0.99999999999789, 0.99999999999946, 0.99999999287551, 0.99999876302649,
0.46903147501117, 0.98835168988253, 0.99994427085086, 0.45235035271542,
0.93496741877335, 0.99999999989803, 0.99999999999781, 0.99999999999948,
0.99999999318224, 0.99994254156311, 0.46891362282273, 0.93382613917348,
0.99994594904099, 0.93002915596843, 0.93569767251247, 0.99999999989658,
0.99999999998074, 0.99999999999946, 0.99999999272802, 0.99999871586781,
0.76935240919896, 0.99002587758346, 0.99999881589732, 0.46179415706093,
0.93417422376389, 0.99999999989735, 0.99999999999789, 0.99999999999946,
0.99999999289347, 0.99999876940486, 0.46930769326427, 0.98837353639905,
0.99994447154714, 0.16313586712094, 0.93500824170148, 0.99999999989744,
0.99999999999789, 0.99999999999946, 0.99999999289347, 0.99999876940486,
0.46930769326427, 0.98837353639905, 0.99994447154714, 0.16330039178981,
0.93500824170148, 0.99999999989803, 0.99999999999781, 0.99999999999948,
0.99999999316541, 0.99994254156311, 0.46794586553266, 0.93382613917348,
0.99994594904099, 0.9303627789484, 0.93569767251247, 0.99999999989778,
0.9999999999978, 0.99999999999948, 0.99999999311433, 0.99999878195152,
0.47101897739483, 0.93368891853679, 0.99994556595217, 0.7571113417265,
0.93553999975802, 0.99999999998191, 0.99999999999784, 0.99999999999971,
0.99999891129658, 0.99994309267792, 0.46510628979591, 0.93442584181035,
0.99894450514543, 0.99890078483692, 0.76933812306423), receivedPower_dbm = c(-93.023492290586,
-92.388378035287, -92.205716340607, -93.816400586752, -95.023489422885,
-100.86308557253, -98.464763536915, -96.175707680373, -102.06189538385,
-99.716653422746, -93.023492290586, -92.384760627397, -92.205716340607,
-93.816400586752, -95.023489422885, -100.86308557253, -98.464201120719,
-96.175707680373, -102.06189538385, -99.717150021506, -93.022927803442,
-92.404017215549, -92.204561341714, -93.814319484729, -95.016990717792,
-102.01669022332, -98.558088145955, -96.173817001483, -102.07406915124,
-99.71517574876, -93.021813165972, -92.409586309743, -92.20229160243,
-93.805335867418, -96.184419849593, -102.01709540787, -99.728735187547,
-96.163233028048, -99.772547164798, -99.706399753853, -93.024204617071,
-92.745813384859, -92.206884754512, -93.818508150122, -95.027018807793,
-100.87000577258, -98.467607232407, -95.005311380324, -102.04157607608,
-99.724619517, -93.022927803442, -92.404017215549, -92.204561341714,
-93.813803344588, -95.015606885523, -102.0157405687, -98.556982278361,
-96.172566862738, -103.21871579865, -99.714687230796, -93.022787428238,
-92.404017215549, -92.204274688493, -93.813803344588, -95.015606885523,
-102.0157405687, -98.556982278361, -96.172566862738, -103.21784988098,
-99.714687230796, -93.021813165972, -92.409950613665, -92.20229160243,
-93.805838770576, -96.184419849593, -102.02042267497, -99.728735187547,
-96.163233028048, -99.768774335378, -99.706399753853, -93.022228914406,
-92.411048503835, -92.203136463155, -93.807357409082, -95.012865008237,
-102.00985717796, -99.730352912911, -96.165675535906, -100.92744056572,
-99.708301333236, -92.735781110993, -92.408137395049, -92.119533319039,
-94.982938427575, -96.181073124017, -102.03018610927, -99.721633629806,
-97.32940323644, -97.347613268692, -100.87007386786), snr = c(49.848348091678,
57.698190927109, 60.17669971462, 41.529809724535, 31.452202106925,
8.1976890851341, 14.240447804094, 24.122884195464, 6.2202875499406,
10.674183333671, 49.848348091678, 57.746270018264, 60.17669971462,
41.529809724535, 31.452202106925, 8.1976890851341, 14.242292077376,
24.122884195464, 6.2202875499406, 10.672962852322, 49.854827699773,
57.49079026127, 60.192705735317, 41.549715223147, 31.499301851462,
6.2853718719014, 13.937702343688, 24.133388256416, 6.2028757927148,
10.677815810561, 49.867624820879, 57.417115267867, 60.224172277442,
41.635752021705, 24.074540962859, 6.2847854917092, 10.644529778044,
24.19227425387, 10.537686730745, 10.699414795917, 49.84017267426,
53.139646558768, 60.160512118809, 41.509660845114, 31.42665220053,
8.1846370024428, 14.231126423354, 31.584125885363, 6.2494585568733,
10.654622041348, 49.854827699773, 57.49079026127, 60.192705735317,
41.55465351989, 31.509340361646, 6.2867464196657, 13.941251828322,
24.140336174865, 4.765718874642, 10.679016976694, 49.856439162736,
57.49079026127, 60.196678846453, 41.55465351989, 31.509340361646,
6.2867464196657, 13.941251828322, 24.140336174865, 4.7666691818074,
10.679016976694, 49.867624820879, 57.412299088098, 60.224172277442,
41.630930975211, 24.074540962859, 6.279972363168, 10.644529778044,
24.19227425387, 10.546845071479, 10.699414795917, 49.862851240855,
57.397787176282, 60.212457625018, 41.61637603957, 31.529239767749,
6.2952688513108, 10.640565481982, 24.178672145334, 8.0771089950663,
10.694731030907, 53.262541905639, 57.43627424514, 61.382796189332,
31.747253311549, 24.093100244121, 6.2658701281075, 10.661949889074,
18.495227442305, 18.417839037171, 8.1845086722809), frameId = c(15051,
15106, 15165, 15220, 15279, 15330, 15385, 15452, 15511, 15566,
15019, 15074, 15129, 15184, 15239, 15298, 15353, 15412, 15471,
15526, 14947, 14994, 15057, 15112, 15171, 15226, 15281, 15332,
15391, 15442, 14971, 15030, 15085, 15144, 15203, 15262, 15321,
15380, 15435, 15490, 14915, 14978, 15033, 15092, 15147, 15198,
15257, 15312, 15371, 15430, 14975, 15034, 15089, 15140, 15195,
15254, 15313, 15368, 15427, 15478, 14987, 15046, 15105, 15160,
15215, 15274, 15329, 15384, 15447, 15506, 14943, 15002, 15061,
15116, 15171, 15230, 15285, 15344, 15399, 15454, 14971, 15026,
15081, 15136, 15195, 15258, 15313, 15368, 15423, 15478, 15039,
15094, 15149, 15204, 15263, 15314, 15369, 15428, 15487, 15546
), packetOkSinr = c(0.99999999314881, 0.9999999998736, 0.99999999996428,
0.99999952114066, 0.99991568416005, 3.00628034688444e-08,
0.51497487795954, 0.99627877136019, 0, 0.011303253101957,
0.99999999314881, 0.99999999987726, 0.99999999996428, 0.99999952114066,
0.99991568416005, 3.00628034688444e-08, 0.51530974419663,
0.99627877136019, 0, 0.011269851265775, 0.9999999931708,
0.99999999985986, 0.99999999996428, 0.99999952599145, 0.99991770469509,
0, 0.45861812482641, 0.99629897628155, 0, 0.011403119534097,
0.99999999321568, 0.99999999985437, 0.99999999996519, 0.99999954639936,
0.99618434878558, 0, 0.010513119213425, 0.99641022914441,
0.00801687746446111, 0.012011103529927, 0.9999999931195,
0.99999999871861, 0.99999999996428, 0.99999951617905, 0.99991456738049,
2.6525298291169e-08, 0.51328066587104, 0.9999212220316, 0,
0.010777054258914, 0.9999999931708, 0.99999999985986, 0.99999999996428,
0.99999952718674, 0.99991812902805, 0, 0.45929307038653,
0.99631228046814, 0, 0.011436292559188, 0.99999999317629,
0.99999999985986, 0.99999999996428, 0.99999952718674, 0.99991812902805,
0, 0.45929307038653, 0.99631228046814, 0, 0.011436292559188,
0.99999999321568, 0.99999999985437, 0.99999999996519, 0.99999954527918,
0.99618434878558, 0, 0.010513119213425, 0.99641022914441,
0.00821047996950475, 0.012011103529927, 0.99999999319919,
0.99999999985345, 0.99999999996519, 0.99999954188106, 0.99991896371849,
0, 0.010410830482692, 0.996384831822, 9.12484388049251e-09,
0.011877185067536, 0.99999999879646, 0.9999999998562, 0.99999999998077,
0.99992756868677, 0.9962208785486, 0, 0.010971897073662,
0.93214999078663, 0.92943956665979, 2.64925478221656e-08),
snir = c(49.848348091678, 57.698190927109, 60.17669971462,
41.529809724535, 31.452202106925, 8.1976890851341, 14.240447804094,
24.122884195464, 6.2202875499406, 10.674183333671, 49.848348091678,
57.746270018264, 60.17669971462, 41.529809724535, 31.452202106925,
8.1976890851341, 14.242292077376, 24.122884195464, 6.2202875499406,
10.672962852322, 49.854827699773, 57.49079026127, 60.192705735317,
41.549715223147, 31.499301851462, 6.2853718719014, 13.937702343688,
24.133388256416, 6.2028757927148, 10.677815810561, 49.867624820879,
57.417115267867, 60.224172277442, 41.635752021705, 24.074540962859,
6.2847854917092, 10.644529778044, 24.19227425387, 10.537686730745,
10.699414795917, 49.84017267426, 53.139646558768, 60.160512118809,
41.509660845114, 31.42665220053, 8.1846370024428, 14.231126423354,
31.584125885363, 6.2494585568733, 10.654622041348, 49.854827699773,
57.49079026127, 60.192705735317, 41.55465351989, 31.509340361646,
6.2867464196657, 13.941251828322, 24.140336174865, 4.765718874642,
10.679016976694, 49.856439162736, 57.49079026127, 60.196678846453,
41.55465351989, 31.509340361646, 6.2867464196657, 13.941251828322,
24.140336174865, 4.7666691818074, 10.679016976694, 49.867624820879,
57.412299088098, 60.224172277442, 41.630930975211, 24.074540962859,
6.279972363168, 10.644529778044, 24.19227425387, 10.546845071479,
10.699414795917, 49.862851240855, 57.397787176282, 60.212457625018,
41.61637603957, 31.529239767749, 6.2952688513108, 10.640565481982,
24.178672145334, 8.0771089950663, 10.694731030907, 53.262541905639,
57.43627424514, 61.382796189332, 31.747253311549, 24.093100244121,
6.2658701281075, 10.661949889074, 18.495227442305, 18.417839037171,
8.1845086722809), ookSnirBer = c(8.8808636558081e-24, 3.2219795637026e-27,
2.6468895519653e-28, 3.9807779074715e-20, 1.0849324265615e-15,
2.5705217057696e-05, 4.7313805615763e-08, 1.8800438086075e-12,
0.00021005320203921, 1.9147343768384e-06, 8.8808636558081e-24,
3.0694773489537e-27, 2.6468895519653e-28, 3.9807779074715e-20,
1.0849324265615e-15, 2.5705217057696e-05, 4.7223753038869e-08,
1.8800438086075e-12, 0.00021005320203921, 1.9171738578051e-06,
8.8229427230445e-24, 3.9715925056443e-27, 2.6045198111088e-28,
3.9014083702734e-20, 1.0342658440386e-15, 0.00019591630514278,
6.4692014108683e-08, 1.8600094209271e-12, 0.0002140067535655,
1.9074922485477e-06, 8.7096574467175e-24, 4.2779443633862e-27,
2.5231916788231e-28, 3.5761615214425e-20, 1.9750692814982e-12,
0.0001960392878411, 1.9748966344895e-06, 1.7515881895994e-12,
2.2078334799411e-06, 1.8649940680806e-06, 8.954486301678e-24,
3.2021085732779e-25, 2.690441113724e-28, 4.0627628846548e-20,
1.1134484878561e-15, 2.6061691733331e-05, 4.777159157954e-08,
9.4891388749738e-16, 0.00020359398491544, 1.9542110660398e-06,
8.8229427230445e-24, 3.9715925056443e-27, 2.6045198111088e-28,
3.8819641115984e-20, 1.0237769828158e-15, 0.00019562832342849,
6.4455095380046e-08, 1.8468752030971e-12, 0.0010099091367628,
1.9051035165106e-06, 8.8085966897635e-24, 3.9715925056443e-27,
2.594108048185e-28, 3.8819641115984e-20, 1.0237769828158e-15,
0.00019562832342849, 6.4455095380046e-08, 1.8468752030971e-12,
0.0010088638355194, 1.9051035165106e-06, 8.7096574467175e-24,
4.2987746909572e-27, 2.5231916788231e-28, 3.593647329558e-20,
1.9750692814982e-12, 0.00019705170257492, 1.9748966344895e-06,
1.7515881895994e-12, 2.1868296425817e-06, 1.8649940680806e-06,
8.7517439682173e-24, 4.3621551072316e-27, 2.553168170837e-28,
3.6469582463164e-20, 1.0032983660212e-15, 0.00019385229409318,
1.9830820164805e-06, 1.7760568361323e-12, 2.919419915209e-05,
1.8741284335866e-06, 2.8285944348148e-25, 4.1960751547207e-27,
7.8468215407139e-29, 8.0407329049747e-16, 1.9380328071065e-12,
0.00020004849911333, 1.9393279417733e-06, 5.9354475879597e-10,
6.4258355913627e-10, 2.6065221215415e-05), ookSnrBer = c(8.8808636558081e-24,
3.2219795637026e-27, 2.6468895519653e-28, 3.9807779074715e-20,
1.0849324265615e-15, 2.5705217057696e-05, 4.7313805615763e-08,
1.8800438086075e-12, 0.00021005320203921, 1.9147343768384e-06,
8.8808636558081e-24, 3.0694773489537e-27, 2.6468895519653e-28,
3.9807779074715e-20, 1.0849324265615e-15, 2.5705217057696e-05,
4.7223753038869e-08, 1.8800438086075e-12, 0.00021005320203921,
1.9171738578051e-06, 8.8229427230445e-24, 3.9715925056443e-27,
2.6045198111088e-28, 3.9014083702734e-20, 1.0342658440386e-15,
0.00019591630514278, 6.4692014108683e-08, 1.8600094209271e-12,
0.0002140067535655, 1.9074922485477e-06, 8.7096574467175e-24,
4.2779443633862e-27, 2.5231916788231e-28, 3.5761615214425e-20,
1.9750692814982e-12, 0.0001960392878411, 1.9748966344895e-06,
1.7515881895994e-12, 2.2078334799411e-06, 1.8649940680806e-06,
8.954486301678e-24, 3.2021085732779e-25, 2.690441113724e-28,
4.0627628846548e-20, 1.1134484878561e-15, 2.6061691733331e-05,
4.777159157954e-08, 9.4891388749738e-16, 0.00020359398491544,
1.9542110660398e-06, 8.8229427230445e-24, 3.9715925056443e-27,
2.6045198111088e-28, 3.8819641115984e-20, 1.0237769828158e-15,
0.00019562832342849, 6.4455095380046e-08, 1.8468752030971e-12,
0.0010099091367628, 1.9051035165106e-06, 8.8085966897635e-24,
3.9715925056443e-27, 2.594108048185e-28, 3.8819641115984e-20,
1.0237769828158e-15, 0.00019562832342849, 6.4455095380046e-08,
1.8468752030971e-12, 0.0010088638355194, 1.9051035165106e-06,
8.7096574467175e-24, 4.2987746909572e-27, 2.5231916788231e-28,
3.593647329558e-20, 1.9750692814982e-12, 0.00019705170257492,
1.9748966344895e-06, 1.7515881895994e-12, 2.1868296425817e-06,
1.8649940680806e-06, 8.7517439682173e-24, 4.3621551072316e-27,
2.553168170837e-28, 3.6469582463164e-20, 1.0032983660212e-15,
0.00019385229409318, 1.9830820164805e-06, 1.7760568361323e-12,
2.919419915209e-05, 1.8741284335866e-06, 2.8285944348148e-25,
4.1960751547207e-27, 7.8468215407139e-29, 8.0407329049747e-16,
1.9380328071065e-12, 0.00020004849911333, 1.9393279417733e-06,
5.9354475879597e-10, 6.4258355913627e-10, 2.6065221215415e-05
)), class = "data.frame", row.names = c(NA, -100L), .Names = c("run",
"repetition", "module", "configname", "packetByteLength", "numVehicles",
"dDistance", "time", "distanceToTx", "headerNoError", "receivedPower_dbm",
"snr", "frameId", "packetOkSinr", "snir", "ookSnirBer", "ookSnrBer"
))
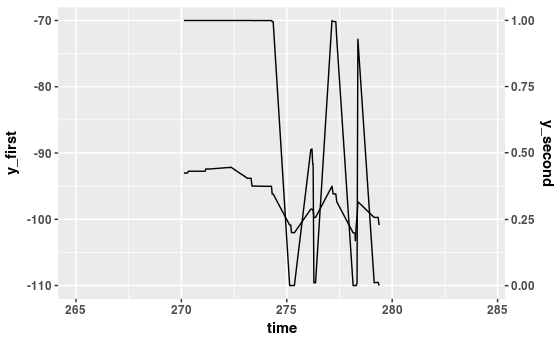
Нахождение функции преобразования
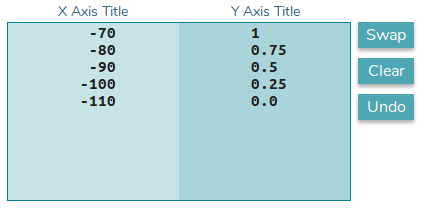
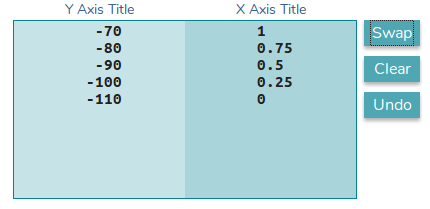
- y1 -> y2 Эта функция используется для преобразования данных вторичной оси y в "нормализацию" в соответствии с первой осью y
функция преобразования: f(y1) = 0.025*x + 2.75
- y2 -> y1 Эта функция используется для преобразования точек разрыва первой оси y в значения второй оси y. Обратите внимание, что ось поменялась местами.
функция преобразования: f(y1) = 40*x - 110
Заговор
Обратите внимание, как функции преобразования используются в ggplot вызов для преобразования данных "на лету"
ggplot(data=combined_80_8192 %>% filter (time > 270, time < 280), aes(x=time) ) +
stat_summary(aes(y=receivedPower_dbm ), fun.y=mean, geom="line", colour="black") +
stat_summary(aes(y=packetOkSinr*40 - 110 ), fun.y=mean, geom="line", colour="black", position = position_dodge(width=10)) +
scale_x_continuous() +
scale_y_continuous(breaks = seq(-0,-110,-10), "y_first", sec.axis=sec_axis(~.*0.025+2.75, name="y_second") )
Первый stat_summary call - это тот, который устанавливает базу для первой оси y. Второй stat_summary Вызов вызывается для преобразования данных. Помните, что все данные будут взяты за первую ось Y. Так что данные должны быть нормализованы для первой оси у. Для этого я использую функцию преобразования данных: y=packetOkSinr*40 - 110
Теперь для преобразования второй оси я использую противоположную функцию внутри scale_y_continuous вызов: sec.axis=sec_axis(~.*0.025+2.75, name="y_second"),
Всегда есть способ.
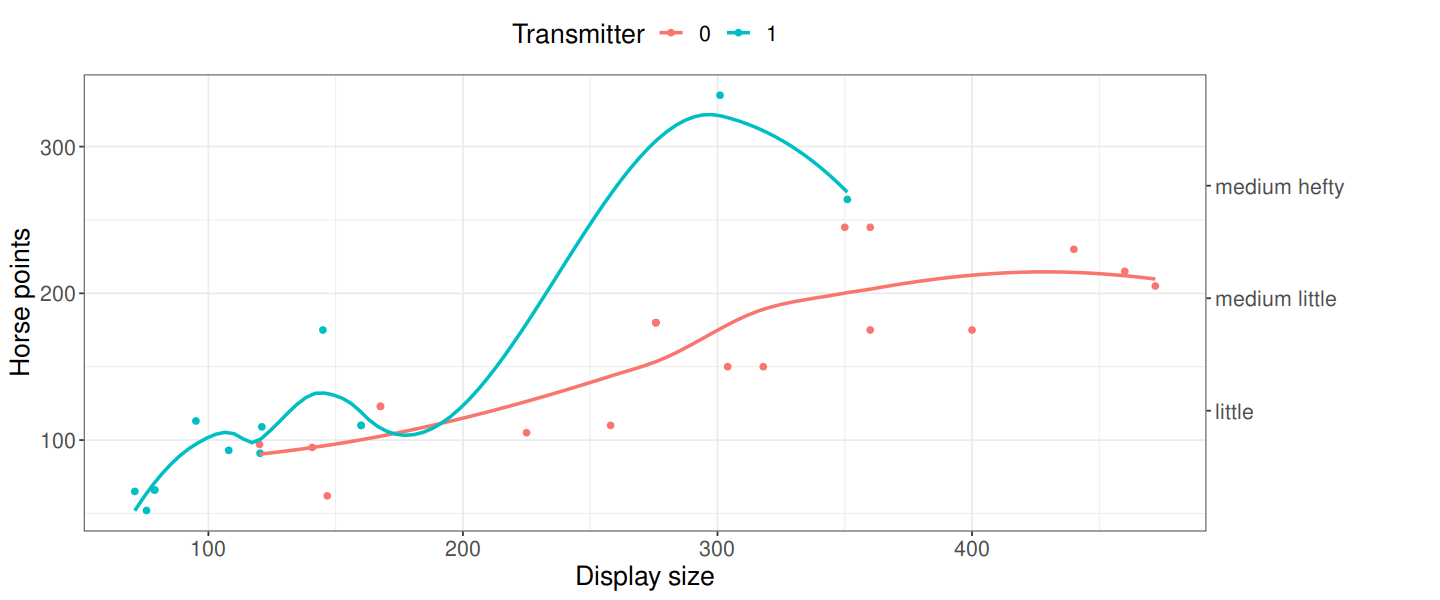
Вот решение, которое позволяет использовать абсолютно произвольные оси без изменения масштаба. Идея состоит в том, чтобы сгенерировать два графика, идентичных за исключением оси, и соединить их вместе с помощью
insert_yaxis_grobа также
get_y_axisфункции в
cowplotупаковка.
library(ggplot2)
library(cowplot)
## first plot
p1 <- ggplot(mtcars,aes(disp,hp,color=as.factor(am))) +
geom_point() + theme_bw() + theme(legend.position='top', text=element_text(size=16)) +
ylab("Horse points" )+ xlab("Display size") + scale_color_discrete(name='Transmitter') +
stat_smooth(se=F)
## same plot with different, arbitrary scale
p2 <- p1 +
scale_y_continuous(position='right',breaks=seq(120,173,length.out = 3),
labels=c('little','medium little','medium hefty'))
ggdraw(insert_yaxis_grob(p1,get_y_axis(p2,position='right')))
Мы определенно могли бы построить график с двумя осями Y, используя функцию base R plot,
# pseudo dataset
df <- data.frame(x = seq(1, 1000, 1), y1 = sample.int(100, 1000, replace=T), y2 = sample(50, 1000, replace = T))
# plot first plot
with(df, plot(y1 ~ x, col = "red"))
# set new plot
par(new = T)
# plot second plot, but without axis
with(df, plot(y2 ~ x, type = "l", xaxt = "n", yaxt = "n", xlab = "", ylab = ""))
# define y-axis and put y-labs
axis(4)
with(df, mtext("y2", side = 4))
Казалось бы, это простой вопрос, но он связан с двумя фундаментальными вопросами. A) Как работать с мультискалярными данными при представлении в сравнительной диаграмме, и, во-вторых, B) можно ли это сделать без некоторых практических правил программирования R, таких как i) плавление данных, ii) огранка, iii) добавление другой слой к существующему. Приведенное ниже решение удовлетворяет обоим вышеперечисленным условиям, поскольку оно обрабатывает данные без необходимости их масштабирования, и, во-вторых, упомянутые методы не используются.
Для тех, кто хочет узнать больше об этом методе, перейдите по ссылке ниже. Как построить 2-осевую диаграмму с столбцами рядом без повторного масштабирования данных
Ты можешь использовать facet_wrap(~ variable, ncol= ) на переменную, чтобы создать новое сравнение. Это не на одной оси, но это похоже.
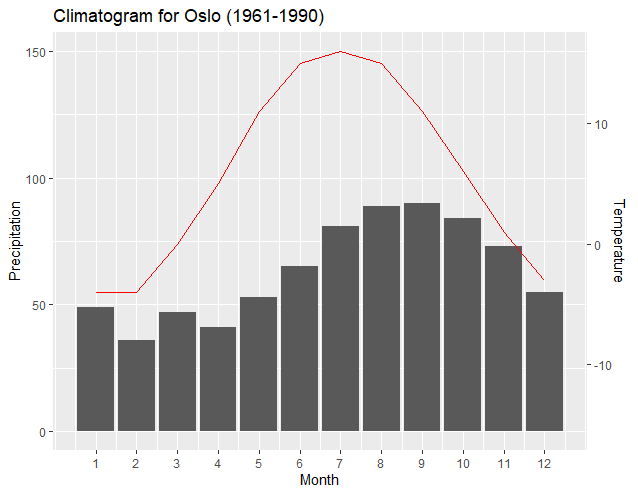
Следующее включает основные данные и программирование , улучшает стратегию по созданию «функции преобразования» для оптимального объединения графиков и оси данных и отвечает на примечание о том, что такая функция может быть создана в R .
#Climatogram for Oslo (1961-1990)
climate <- tibble(
Month = 1:12,
Temp = c(-4,-4,0,5,11,15,16,15,11,6,1,-3),
Precip = c(49,36,47,41,53,65,81,89,90,84,73,55))
#y1 identifies the position, relative to the y1 axis,
#the locations of the minimum and maximum of the y2 graph.
#Usually this will be the min and max of y1.
#y1<-(c(max(climate$Precip), 0))
#y1<-(c(150, 55))
y1<-(c(max(climate$Precip), min(climate$Precip)))
#y2 is the Minimum and maximum of the secondary axis data.
y2<-(c(max(climate$Temp), min(climate$Temp)))
#axis combines y1 and y2 into a dataframe used for regressions.
axis<-cbind(y1,y2)
axis<-data.frame(axis)
#Regression of Temperature to Precipitation:
T2P<-lm(formula = y1 ~ y2, data = axis)
T2P_summary <- summary(lm(formula = y1 ~ y2, data = axis))
T2P_summary
#Identifies the intercept and slope of regressing Temperature to Precipitation:
T2PInt<-T2P_summary$coefficients[1, 1]
T2PSlope<-T2P_summary$coefficients[2, 1]
#Regression of Precipitation to Temperature:
P2T<-lm(formula = y2 ~ y1, data = axis)
P2T_summary <- summary(lm(formula = y2 ~ y1, data = axis))
P2T_summary
#Identifies the intercept and slope of regressing Precipitation to Temperature:
P2TInt<-P2T_summary$coefficients[1, 1]
P2TSlope<-P2T_summary$coefficients[2, 1]
#Create Plot:
ggplot(climate, aes(Month, Precip)) +
geom_col() +
geom_line(aes(y = T2PSlope*Temp + T2PInt), color = "red") +
scale_y_continuous("Precipitation", sec.axis = sec_axis(~.*P2TSlope + P2TInt, name = "Temperature")) +
scale_x_continuous("Month", breaks = 1:12) +
theme(axis.line.y.right = element_line(color = "red"),
axis.ticks.y.right = element_line(color = "red"),
axis.text.y.right = element_text(color = "red"),
axis.title.y.right = element_text(color = "red")) +
ggtitle("Climatogram for Oslo (1961-1990)")
Наиболее примечательно то, что новая «функция преобразования» работает лучше всего с двумя точками данных из набора данных каждой оси - обычно с максимальным и минимальным значениями каждого набора. Результирующие наклоны и пересечения двух регрессий позволяют ggplot2 точно сопоставлять графики минимумов и максимумов каждой оси. Как отметил , две регрессии преобразуют каждый набор данных и график в другой. Один преобразует точки разрыва первой оси y в значения второй оси y. Второй преобразует данные вторичной оси y, чтобы они были «нормализованы» согласно первой оси y. Следующий вывод показывает, как ось выравнивает минимумы и максимумы каждого набора данных:
Соответствие максимумов и минимумов может быть наиболее подходящим; однако еще одно преимущество этого метода состоит в том, что график, связанный со вторичной осью, можно легко сместить, если это необходимо, путем изменения строки программирования, связанной с данными первичной оси. Выходные данные ниже просто изменяют ввод минимального количества осадков в строке программирования y1 на «0» и, таким образом, выравнивают минимальный уровень температуры с уровнем осадков «0».
От: y1 <- (c (max (климат $ Precip), min (климат $ Precip)))
Кому: y1 <- (c (max (климат $ Precip), 0))
Обратите внимание, как полученные новые регрессии и ggplot2 автоматически скорректировали график и ось, чтобы правильно выровнять минимальную температуру с новой «базой» уровня осадков «0». Точно так же можно легко поднять график температуры, чтобы он был более очевидным. Следующий график создается простым изменением указанной выше строки на:
"y1 <- (c (150, 55))"
Вышеупомянутая линия указывает, что максимум на графике температуры должен совпадать с уровнем осадков «150», а минимум на температурной линии - с уровнем осадков «55». Опять же, обратите внимание, как ggplot2 и полученные новые результаты регрессии позволяют графику поддерживать правильное выравнивание с осью.
Вышеупомянутое может быть нежелательным результатом; однако это пример того, как можно легко манипулировать графиком и при этом поддерживать правильные отношения между графиками и осью. Включение Дага Хьерманатемы Дага Хьерманастроятuser4786271баптистаuser4786271 улучшает идентификацию оси, соответствующей сюжету.
Я признаю и согласен с Хэдли (и другими), что отдельные y-шкалы "в корне ошибочны". Сказав это - я часто желаю ggplot2 была особенность - особенно, когда данные в широкоформатном формате, и я быстро хочу визуализировать или проверить данные (т.е. только для личного использования).
В то время как tidyverse библиотека позволяет довольно легко преобразовать данные в длинный формат (такой, что facet_grid() будет работать), процесс все еще не тривиален, как видно ниже:
library(tidyverse)
df.wide %>%
# Select only the columns you need for the plot.
select(date, column1, column2, column3) %>%
# Create an id column – needed in the `gather()` function.
mutate(id = n()) %>%
# The `gather()` function converts to long-format.
# In which the `type` column will contain three factors (column1, column2, column3),
# and the `value` column will contain the respective values.
# All the while we retain the `id` and `date` columns.
gather(type, value, -id, -date) %>%
# Create the plot according to your specifications
ggplot(aes(x = date, y = value)) +
geom_line() +
# Create a panel for each `type` (ie. column1, column2, column3).
# If the types have different scales, you can use the `scales="free"` option.
facet_grid(type~., scales = "free")
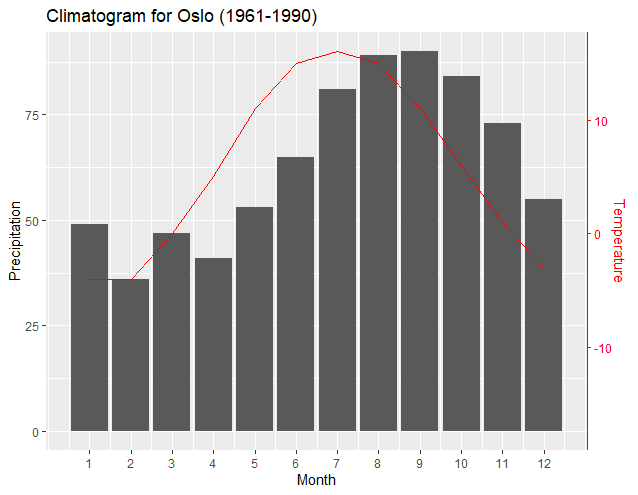
Я обнаружил, что этот ответ помог мне больше всего, но обнаружил, что были некоторые крайние случаи, которые, похоже, не обрабатывались правильно, в определенных отрицательных случаях, а также случай, когда мои пределы имели нулевое расстояние (что может произойти, если мы наши пределы от макс / мин данных). Тестирование показывает, что это работает стабильно.
Я использую следующий код. Здесь я предполагаю, что у нас есть [x1,x2], который мы хотим преобразовать в [y1,y2]. Я сделал это так, чтобы преобразовать [x1,x2] в [0,1] (достаточно простое преобразование), затем [0,1] в [y1,y2].
climate <- tibble(
Month = 1:12,
Temp = c(-4,-4,0,5,11,15,16,15,11,6,1,-3),
Precip = c(49,36,47,41,53,65,81,89,90,84,73,55)
)
#Set the limits of each axis manually:
ylim.prim <- c(0, 180) # in this example, precipitation
ylim.sec <- c(-4, 18) # in this example, temperature
b <- diff(ylim.sec)/diff(ylim.prim)
#If all values are the same this messes up the transformation, so we need to modify it here
if(b==0){
ylim.sec <- c(ylim.sec[1]-1, ylim.sec[2]+1)
b <- diff(ylim.sec)/diff(ylim.prim)
}
if (is.na(b)){
ylim.prim <- c(ylim.prim[1]-1, ylim.prim[2]+1)
b <- diff(ylim.sec)/diff(ylim.prim)
}
ggplot(climate, aes(Month, Precip)) +
geom_col() +
geom_line(aes(y = ylim.prim[1]+(Temp-ylim.sec[1])/b), color = "red") +
scale_y_continuous("Precipitation", sec.axis = sec_axis(~((.-ylim.prim[1]) *b + ylim.sec[1]), name = "Temperature"), limits = ylim.prim) +
scale_x_continuous("Month", breaks = 1:12) +
ggtitle("Climatogram for Oslo (1961-1990)")
Ключевыми частями здесь являются то, что мы трансформируем вторичную ось y с помощью ~((.-ylim.prim[1]) *b + ylim.sec[1]) а затем примените обратное к фактическим значениям y = ylim.prim[1]+(Temp-ylim.sec[1])/b). Мы также должны убедиться, чтоlimits = ylim.prim.
Ответ Хэдли дает интересную ссылку на отчет Стивена Фью " Двойные оси в графах". Являются ли они когда-либо лучшим решением?,
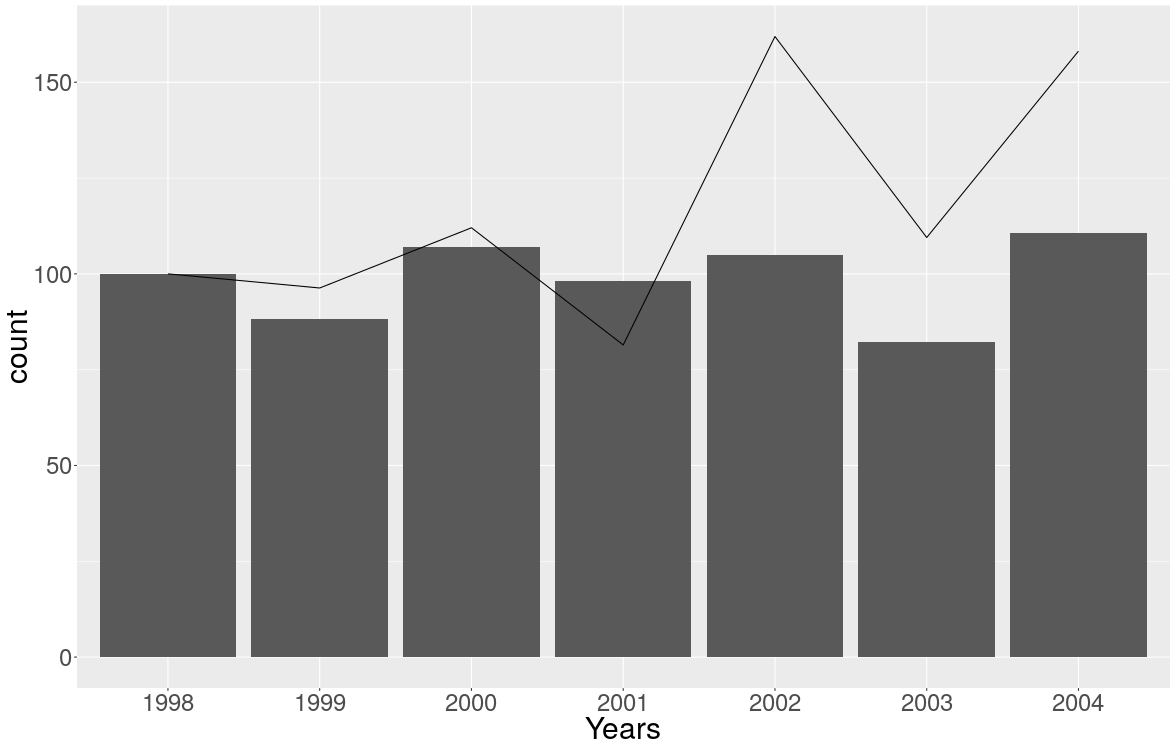
Я не знаю, что означает OP с "счетами" и "скоростью", но быстрый поиск дает мне " Счет и скорость", поэтому я получаю некоторые данные об авариях в североамериканском альпинизме 1:
Years<-c("1998","1999","2000","2001","2002","2003","2004")
Persons.Involved<-c(281,248,301,276,295,231,311)
Fatalities<-c(20,17,24,16,34,18,35)
rate=100*Fatalities/Persons.Involved
df<-data.frame(Years=Years,Persons.Involved=Persons.Involved,Fatalities=Fatalities,rate=rate)
print(df,row.names = FALSE)
Years Persons.Involved Fatalities rate
1998 281 20 7.117438
1999 248 17 6.854839
2000 301 24 7.973422
2001 276 16 5.797101
2002 295 34 11.525424
2003 231 18 7.792208
2004 311 35 11.254019
И затем я попытался сделать график, как предложили несколько на странице 7 вышеупомянутого отчета (и следуя запросу OP, чтобы построить график в виде гистограммы и ставок в виде линейного графика):
Другое менее очевидное решение, которое работает только для временных рядов, заключается в преобразовании всех наборов значений в общую количественную шкалу путем отображения процентных различий между каждым значением и справочным (или индексным) значением. Например, выберите конкретный момент времени, например, первый интервал, который отображается на графике, и выразите каждое последующее значение как процентную разницу между ним и начальным значением. Это делается путем деления значения в каждый момент времени на значение для начального момента времени, а затем умножения его на 100, чтобы преобразовать ставку в процент, как показано ниже.
df2<-df
df2$Persons.Involved <- 100*df$Persons.Involved/df$Persons.Involved[1]
df2$rate <- 100*df$rate/df$rate[1]
plot(ggplot(df2)+
geom_bar(aes(x=Years,weight=Persons.Involved))+
geom_line(aes(x=Years,y=rate,group=1))+
theme(text = element_text(size=30))
)
Но мне это не очень нравится, и я не могу легко поставить легенду...
1 УИЛЬЯМСОН, Джед и др. Аварии в североамериканском альпинизме 2005. Книги альпинистов, 2005.