Ближайшие точки на симплициальном комплексе
Для двух (низкоразмерных, возможно, двумерных) симплициальных комплексов P и Q существует ли эффективный алгоритм построения P', подмножества P, состоящего из всех точек в P, которые являются ближайшей точкой к некоторой точке q в Q?
Например, если бы P и Q были невырожденно пересекающимися отрезками, P'было бы их пересечением; если бы они не пересекались, P'была бы точкой или отрезком. Если бы P был отрезком линии, а Q - треугольником, P'была бы проекцией Q на P. Если бы P был треугольником, а Q была линией, пересекающей P, P' состояла бы из нескольких отрезков падающей линии, изнутри и / или внешность треугольника.
Некоторые примеры рисунков: (ОДИН С ПЕРЕСЕЧЕНИЕМ ТОЧКИ НЕПРАВИЛЬНО)
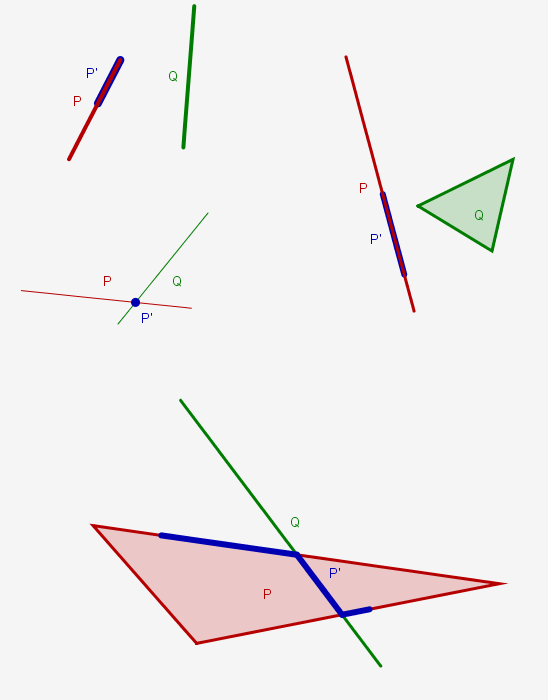
В общем, P', кажется, состоит из проекций Q на каждую грань (любой размерности) P, но это описание включает в себя большое количество граней, в которых преобладают грани более высокой размерности, и мне не ясно, как поступить с этим эффективно.