NLS оставить один сюжет в R

Question

Я пытаюсь сделать одну из перекрестных проверок нелинейной регрессии и построить оптимальное соответствие. Я чувствую, что мои функции loocv и plot абсолютно неверны. Кто-нибудь может уточнить, что я делаю не так?

data(Boston, package='MASS')
y <- Boston$nox
x <- Boston$dis
n <- length(x)
nla <- n
las <- seq(0, .85, length=nla)
cvs <- rep(0, nla)
for(j in 1:nla) {
  prs <- rep(0,n)
  for(i in 1:n) {
    yi <- y[-i]
    xi <- x[-i]
    d <- nls(y~ A + B * exp(C * x), start=list(A=0.5, B=0.5, C=-0.5))
    prs[i] <- predict(d, newdata=data.frame(xi=x[i]))
  }
 cvs[j] <- mean( (y - prs)^2 )
}
cvs[j]
plot(y~x, pch=19, col='gray', cex=1.5,xlab='dis', ylab='nox')
d <- nls(y~ A + B * exp(C * x), start=list(A=0.5, B=0.5, C=-0.5))
lines(predict(d)[order(x)]~sort(x), lwd=4, col='black')

Answer 1

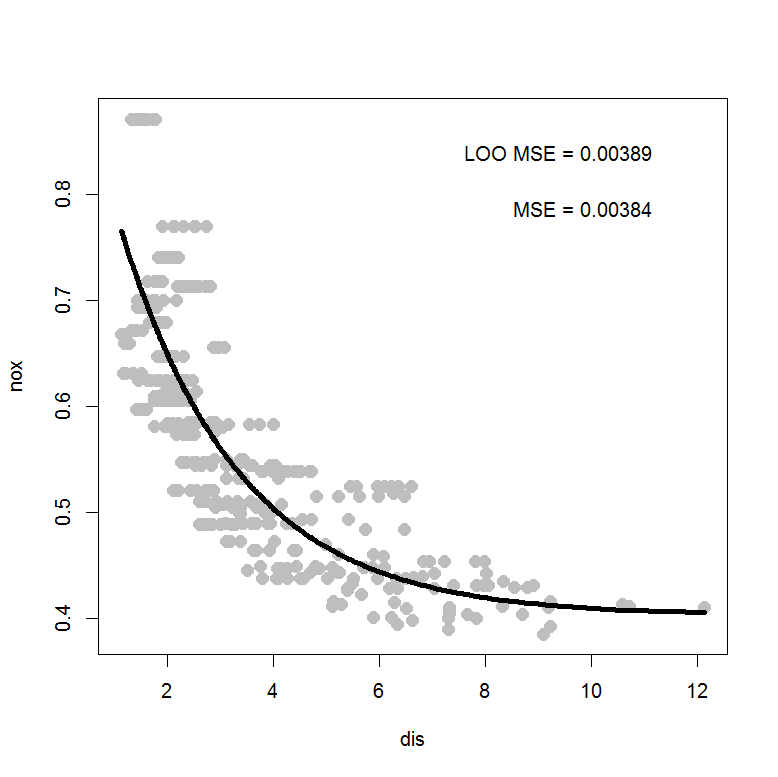
Вы, кажется, были близки, но в вашем цикле вы все еще вызывали полный набор данных x а также y, Насколько я могу судить, вам нужен только один цикл для подгонки модели к каждому сценарию "один на один". Таким образом, я не вижу необходимости в переменных las ни prs, Для справки, график показывает среднеквадратичную ошибку, оставленную без учета (LOO MSE), и среднеквадратичную ошибку невязок (MSE) для модели nls, подходящей для полного набора данных.

Автор сценария:

require(MASS)
data(Boston, package='MASS')
y <- Boston$nox
x <- Boston$dis
n <- length(x)

cvs <- rep(0, n)
for(j in seq(n)){
  ys <- y[-j]
  xs <- x[-j]
  d <- nls(ys ~ A + B * exp(C * xs), start=list(A=0.5, B=0.5, C=-0.5))
  cvs[j] <- (y[j] - predict(d, data.frame(xs=x[j])))^2
  print(paste0(j, " of ", n, " finished (", round(j/n*100), "%)"))
}

plot(y~x, pch=19, col='gray', cex=1.5, xlab='dis', ylab='nox')
d <- nls(y~ A + B * exp(C * x), start=list(A=0.5, B=0.5, C=-0.5))
lines(predict(d)[order(x)]~sort(x), lwd=4, col='black')
usr <- par("usr")
text(usr[1] + 0.9*(usr[2]-usr[1]), usr[3] + 0.9*(usr[4]-usr[3]), paste("LOO MSE", "=", round(mean(cvs), 5)), pos=2)
text(usr[1] + 0.9*(usr[2]-usr[1]), usr[3] + 0.8*(usr[4]-usr[3]), paste("MSE", "=", round(mean(resid(d)^2), 5)), pos=2)