Якобиан нелинейного ОДУ в MATLAB

Question

Я рассчитываю jacobian для задачи двух тел, которая определяется так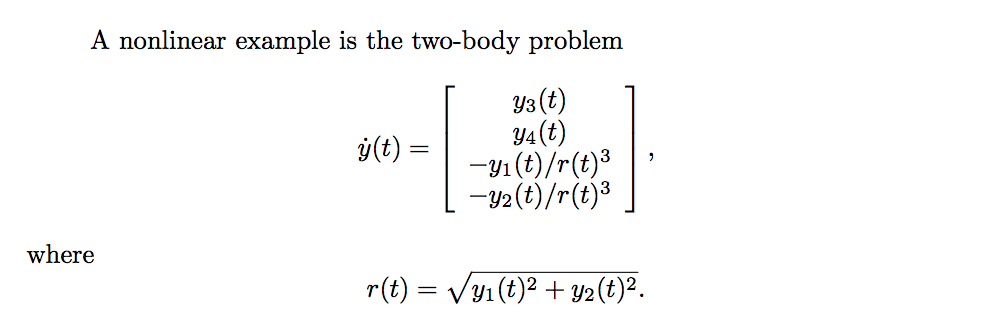

Я настроил свою систему уравнений следующим образом

syms y1(t) y2(t) y3(t) y4(t)

r = sqrt(y1^2 + y2^2)
y3 = diff(y1)
y4 = diff(y2)
yd = [y3; y4; -y1/r^3; -y2/r^3]

jacobian(yd, [y1 y2 y3 y4])

Тем не менее, когда я запускаю jacobian Функция я получаю следующую ошибку

Второй аргумент должен быть вектором переменных.

Что я делаю неправильно?

РЕДАКТИРОВАТЬ:

Я также пытался параметризовать y для т y(t) но безрезультатно.

Answer 1

Поскольку сообщение об ошибке предполагает, что вторым аргументом должен быть вектор переменных, тогда как в вашем случае это: [y1, y2, 1, 1],

Также нет необходимости инициализировать их как symfun класс т.е. y1(t), y2(t), y3(t) а также y4(t)Вы можете определить их как sym класс вместо то есть y1, y2, y3 а также y4

Итак, инициализируя их как sym и удаление строк, где вы делаете y3 а также y4 равно 1т.е.

syms y1 y2 y3 y4
r = sqrt(y1^2 + y2^2);
yd = [y3; y4; -y1/r^3; -y2/r^3];
jacobian(yd, [y1 y2 y3 y4])

вы получите этот вывод:

[                                                    0,                                                    0, 1, 0]
[                                                    0,                                                    0, 0, 1]
[ (3*y1^2)/(y1^2 + y2^2)^(5/2) - 1/(y1^2 + y2^2)^(3/2),                        (3*y1*y2)/(y1^2 + y2^2)^(5/2), 0, 0]
[                        (3*y1*y2)/(y1^2 + y2^2)^(5/2), (3*y2^2)/(y1^2 + y2^2)^(5/2) - 1/(y1^2 + y2^2)^(3/2), 0, 0]