Получите степень свободы для стандартизированного распределения T с MLE

Question

Прежде всего, я заранее благодарю всех за то, что прочитали это.

Я пытаюсь подогнать стандартизированное распределение T-Student (т. Е. T-Student со стандартным отклонением = 1) на серии данных; то есть: я хочу оценить степени свободы с помощью оценки максимального правдоподобия.

Пример того, чего мне нужно достичь, можно найти в следующем (простом) файле Excel, который я создал: https://www.dropbox.com/s/6wv6egzurxh4zap/Excel%20Implementation%20Example.xlsx?dl=0

Внутри файла Excel у меня есть изображение, которое содержит формулу, соответствующую вычислению функции логарифмического правдоподобия для стандартизированного распределения T по студентам. Формула была взята из книги финансов (Элементы управления финансовыми рисками - Питер Кристофферсен).

До сих пор я пробовал это с R:

copula.data <- read.csv(file.choose(),header = TRUE)
z1 <- copula.data[,1]

library(fitdistrplus)


ft1 = fitdist(z1, "t", method = "mle", start = 10)
df1=ft1$estimate[1]

df1
logLik(ft1)

df1 выдает число: 13.11855278779897

logLike (ft1) возвращает число: -3600.2918050056487

Тем не менее, файл Excel дает степени свободы: 8,2962365022727 и логарифмическая вероятность: -3588,8879 (что является правильным ответом).

Примечание. Файл.csv, который читает мой код, выглядит следующим образом: https://www.dropbox.com/s/nnh2jgq4fl6cm12/Data%20for%20T%20Copula.csv?dl=0

Есть идеи? Спасибо, люди!

Answer 1

Формула из вашей таблицы (с n, x заменил параметр df и данные)

= ГАММАНЛОГ ((п + 1) / 2) -GAMMALN(п / 2) -LN(ПИ ()) / 2-LN(п-2)/2-1/2*(1+ N)*LN(1+ х ^2/(п-2))

или возведения в степень,

Гамма ((n+1)/2) / (sqrt((n-2) pi) Гамма (n/2)) (1+x^2/(n-2))^-((n+1)/2)

?dt дает

f(x) = Гамма ((n+1)/2) / (sqrt(n pi) Гамма (n/2)) (1 + x^2/n)^-((n+1)/2)

Таким образом, разница заключается в тех, n-2 значения в двух местах в формуле. У меня недостаточно контекста, чтобы понять, почему автор определяет распределение t таким способом; может быть какая-то веская причина...

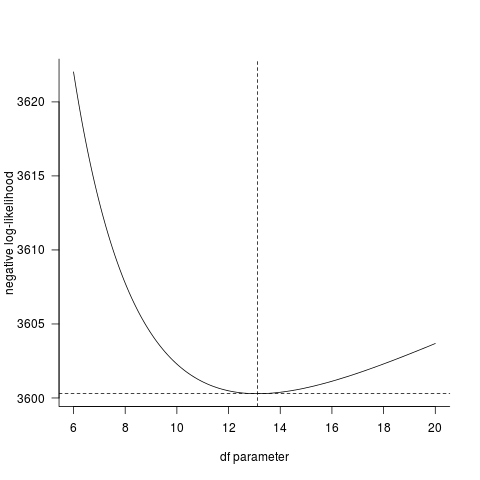
Если посмотреть на кривую отрицательного логарифмического правдоподобия напрямую, то, безусловно, fitdistrplus Ответ согласуется с прямым расчетом. (Было бы очень удивительно, если бы была ошибка в dt() функции, функции распределения R очень широко используются и тщательно протестированы.)

LL <- function(p,data=z1) {
    -sum(dt(data,df=p,log=TRUE))
}
pvec <- seq(6,20,by=0.05)
Lvec <- sapply(pvec,LL)
par(las=1,bty="l")
plot(pvec,Lvec,type="l",
     xlab="df parameter",ylab="negative log-likelihood")
## superimpose fitdistr results ...
abline(v=coef(ft1),lty=2)
abline(h=-logLik(ft1),lty=2)

Если вы не скажете нам что-то еще об определении проблемы, мне кажется, что R получает правильный ответ. (Среднее и sd данных, которые вы дали, не были точно равны 0 и 1 соответственно, но они были близки; центрирование и масштабирование дали еще большее значение для параметра.)