Алгоритм выбора равномерно распределенных точек
Предположим, что в отрезке линии есть 25 точек, и эти точки могут быть неравномерно (пространственно), как показано на следующем рисунке: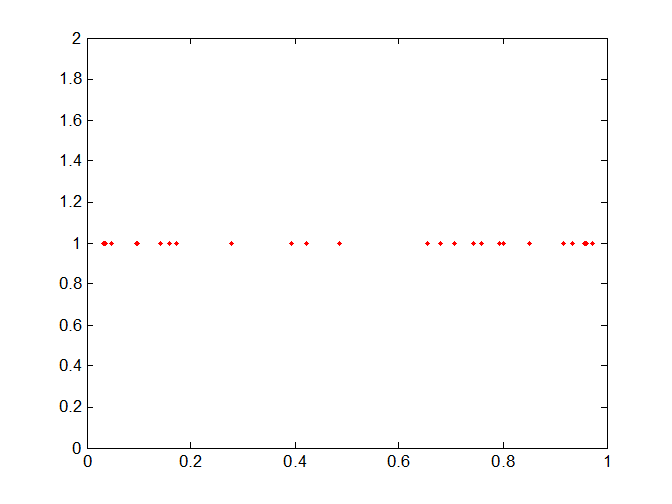
Мой вопрос заключается в том, как мы можем выбрать 10 баллов среди этих 25 баллов, чтобы эти 10 баллов могли быть как можно более равномерно распределены по пространству. В ситуации с идеями выбранные точки должны выглядеть примерно так: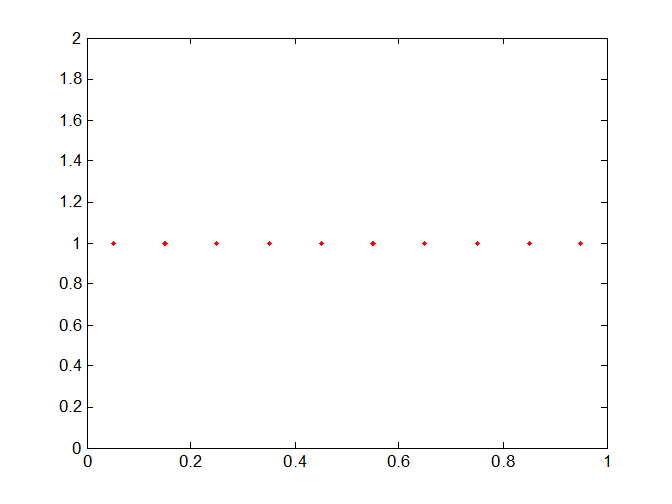
РЕДАКТИРОВАТЬ: Это правда, что этот вопрос может стать более элегантным, если я могу сказать критерий, который оправдывает "равномерное распределение". Что я знаю, так это мое ожидание по выбранным точкам: если я разделю отрезок на 10 равных отрезков. Я ожидаю, что должна быть одна точка на каждом небольшом отрезке. Конечно, может случиться так, что в некоторых небольших отрезках мы не сможем найти репрезентативные точки. В этом случае я прибегну к соседнему небольшому отрезку, который имеет репрезентативную точку. На следующем шаге я разделю выбранный соседний сегмент на две части: если каждая часть имеет репрезентативные точки, то проблема пустых репрезентативных точек будет решена. Если мы не можем найти репрезентативную точку в одном из маленьких отрезков, мы можем еще больше разделить ее на более мелкие части. Или мы можем прибегнуть к следующему соседнему сегменту линии.
РЕДАКТИРОВАТЬ: Используя динамическое программирование, возможное решение реализуется следующим образом:
#include <iostream>
#include <vector>
using namespace std;
struct Note
{
int previous_node;
double cost;
};
typedef struct Note Note;
int main()
{
double dis[25] =
{0.0344460805029088, 0.118997681558377, 0.162611735194631,
0.186872604554379, 0.223811939491137, 0.276025076998578,
0.317099480060861, 0.340385726666133, 0.381558457093008,
0.438744359656398, 0.445586200710900, 0.489764395788231,
0.498364051982143, 0.585267750979777, 0.646313010111265,
0.655098003973841, 0.679702676853675, 0.694828622975817,
0.709364830858073, 0.754686681982361, 0.765516788149002,
0.795199901137063, 0.823457828327293, 0.950222048838355, 0.959743958516081};
Note solutions[25];
for(int i=0; i<25; i++)
{
solutions[i].cost = 1000000;
}
solutions[0].cost = 0;
solutions[0].previous_node = 0;
for(int i=0; i<25; i++)
{
for(int j= i-1; j>=0; j--)
{
double tempcost = solutions[j].cost + std::abs(dis[i]-dis[j]-0.1);
if (tempcost<solutions[i].cost)
{
solutions[i].previous_node = j;
solutions[i].cost = tempcost;
}
}
}
vector<int> selected_points_index;
int i= 24;
selected_points_index.push_back(i);
while (solutions[i].previous_node != 0)
{
i = solutions[i].previous_node;
selected_points_index.push_back(i);
}
selected_points_index.push_back(0);
std::reverse(selected_points_index.begin(),selected_points_index.end());
for(int i=0; i<selected_points_index.size(); i++)
cout<<selected_points_index[i]<<endl;
return 0;
}
Результат показан на следующем рисунке, где выделенные точки обозначены зеленым цветом:

3 ответа
Пусть {x[i]} будет вашим множеством упорядоченных точек. Я думаю, что вам нужно сделать, это найти подмножество из 10 точек {y[i]}, которое минимизирует \sum{|y[i]-y[i-1]-0.1|} с y[-1] = 0,
Теперь, если вы видите конфигурацию в виде сильно связанного ориентированного графа, где каждый узел является одним из 25 двойных, а стоимость каждого ребра равна |y[i]-y[i-1]-0.1|, вы должны иметь возможность решить задачу в O(n^2 +nlogn) времени с помощью алгоритма Дейкстры.
Другая идея, которая, вероятно, приведет к лучшему результату, заключается в использовании динамического программирования: если элемент x [i] является частью нашего решения, общий минимум представляет собой сумму минимума, чтобы добраться до точки x [i] плюс минимум, чтобы получить конечную точку, так что вы можете написать минимальное решение для каждой точки, начиная с наименьшего и используя для следующего минимальное значение между его предшественниками.
Обратите внимание, что вам, вероятно, придется проделать дополнительную работу, чтобы выбрать из набора решений подмножество из тех, у кого есть 10 баллов.
РЕДАКТИРОВАТЬ
Я написал это в C#:
for (int i = 0; i < 25; i++)
{
for (int j = i-1; j > 0; j--)
{
double tmpcost = solution[j].cost + Math.Abs(arr[i] - arr[j] - 0.1);
if (tmpcost < solution[i].cost)
{
solution[i].previousNode = j;
solution[i].cost = tmpcost;
}
}
}
Я не проводил много испытаний, и может возникнуть некоторая проблема, если "дыры" в 25 элементах достаточно широки, что приведет к решениям короче 10 элементов... но это просто для того, чтобы дать вам некоторые идеи работа над:)
Пока хорошо, а наверное O(n^2) решение приходит, используйте это приближение:
Разделите диапазон на 10 бункеров одинакового размера. Выберите точку в каждой ячейке, ближайшую к центру каждой ячейки. Работа выполнена.
Если вы обнаружите, что одна из корзин пуста, выберите меньшее количество корзин и повторите попытку.
Без информации о научной модели, которую вы пытаетесь реализовать, трудно (а) предложить более подходящий алгоритм и / или (б) обосновать вычислительные усилия более сложного алгоритма.
Вы можете найти приближенное решение с помощью алгоритма адаптивного немаксимального подавления (ANMS), если точки взвешены. Алгоритм выбирает n лучших точек, сохраняя их пространственно хорошо распределенными (большинство распределено по пространству).
Я думаю, что вы можете назначить точечные веса на основе вашего критерия распределения - например, расстояние от равномерной решетки по вашему выбору. Я думаю, что решетка должна иметь n-1 бинов для оптимального результата.
Вы можете посмотреть следующие статьи, обсуждающие 2D случай (алгоритм может быть легко реализован в 1D):
Тюрк, Штеффен Гауглиц, Лука Фоскини, Мэтью и Тобиас Хёллер. " ЭФФЕКТИВНО ВЫБОР ПРОСТРАНСТВЕННО РАСПРЕДЕЛЕННЫХ КЛЮЧЕЙ ДЛЯ ВИЗУАЛЬНОГО ОТСЛЕЖИВАНИЯ".
Браун, Мэтью, Ричард Шелиски и Саймон Уиндер. " Сопоставление нескольких изображений с использованием многомасштабных ориентированных исправлений". Computer Vision и Pattern Recognition, 2005. CVPR 2005. IEEE Computer Society Conference on. Том 1. IEEE, 2005.
Второй документ менее связан с вашей проблемой, но он описывает основной алгоритм ANMS. Первые документы обеспечивают более быстрое решение. Я предполагаю, что оба сделают в 1D за умеренное количество очков (~10K).