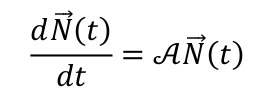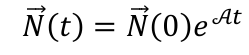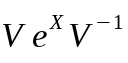Oj-Algo - матрица экспоненциальная

Question

Я решаю следующее уравнение:

Чтобы решить это, я хотел бы использовать экспоненциальную матрицу:

Я думал о 3 способах сделать это:

1. Я мог бы пропустить это, но у Oj-Algo мог быть простой способ вычислить exp(A) (я не нашел его в MatrixStore javadoc)
2. Я получаю матрицы D и V из методов EigenValue ([A] = [V] [D] [V]^-1), а затем вычисляю 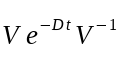Тогда возникает вопрос: как применить функцию x->exp(x*t) ко всем диагональным элементам D?
3. Последняя идея в основном такая же, как и 2. но я предварительно сохраняю скалярно-матричное произведение в новой матрице ([X] = [D]*(-t)), а затем вычисляю:

Можете ли вы помочь мне найти лучший способ / методы / класс, который я должен использовать? Спасибо

NB. Этот вопрос является "последующим вопросом": первый вопрос

РЕДАКТИРОВАТЬ: Это то, что я пытался на данный момент, это лучший способ сделать это?:

import static org.ojalgo.function.PrimitiveFunction.EXP;


public class SolveDifferentialEquationTest
{

    private static final PhysicalStore.Factory<Double, PrimitiveDenseStore> matrixFactory = PrimitiveDenseStore.FACTORY;

    public static void main(String[] args)
    {
        SparseStore<Double> matrix;
        final PhysicalStore<Double> diagMatrix;
        final PhysicalStore<Double> eigenVectorMatrix;
        final PhysicalStore<Double> inverseEigenVectorMatrix;
        final Eigenvalue<Double> eigenvalue;
        final int time = 100;
        PhysicalStore<Double> initialVector;
        final PhysicalStore<Double> finalVector;

        int dim = 2000;
        matrix = SparseStore.PRIMITIVE.make(dim, dim);
        initialVector = matrixFactory.makeZero(dim,1);

        // fill matrix and initialVector
        //...

        //Decompose matrix

        eigenvalue = Eigenvalue.PRIMITIVE.make(matrix);
        eigenvalue.decompose(matrix);
        diagMatrix = eigenvalue.getD().copy();
        eigenVectorMatrix = eigenvalue.getV().copy();
        InverterTask<Double> inverter = InverterTask.PRIMITIVE.make(eigenVectorMatrix);
        try {
            inverseEigenVectorMatrix = inverter.invert(eigenVectorMatrix).copy();
        } catch (RecoverableCondition e) {
            throw new RuntimeException(e);
        }

        // Construct exp(Dt)
        diagMatrix.multiply(time);
        diagMatrix.modifyDiagonal(EXP);

        // Compute
        finalVector = inverseEigenVectorMatrix.multiply(diagMatrix)
                                              .multiply(eigenVectorMatrix)
                                              .multiply(initialVector)
                                              .copy();
    }
}