Быстрый алгоритм для пересечения любых пересекающихся ребер в наборе многоугольников

Question

У меня есть несколько полигонов, каждый из которых представлен в виде списка точек. Я ищу быстрый алгоритм, чтобы пройти список полигонов и пересечь все скрещенные ребра, пока не останется скрещенных ребер.

Псудокод для текущей версии:

While True:
    For each pair of polygons:
         for edge1 in first_polygon:
             for edge2 in second_polygon:
                 if edges_cross(edge1,edge2): # Uses a line segment intersection test
                     uncross_edges(first_polygon,second_polygon,edge1,edge2)
    If no edges have been uncrossed:
        break

Это может быть улучшено путем замены цикла while рекурсией. Тем не менее, он все еще довольно плох с точки зрения производительности.

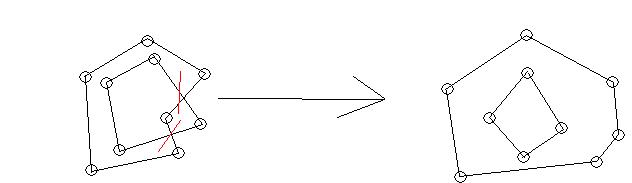
Ниже приведен простой пример распутывания *. На самом деле будет много полигонов и достаточное количество точек на каждый полигон (около 10-500). Красная линия показывает, какие два ребра не пересекаются. Результатом всегда должна быть серия плоских графиков, хотя и не уверен, есть ли несколько действительных результатов или только один.

Редактировать: на этот раз я сначала добавил линии, затем добавил точки и использовал более сложную форму. Притворись, что точки исправлены.

Answer 1

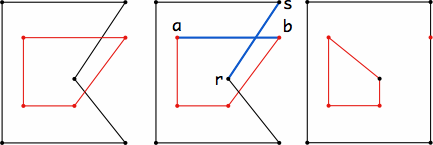
Во-первых, давайте проиллюстрируем, что вы хотите (если я правильно понял). Предположим, у вас есть два полигона, один из которых имеет ребро (a, b) который пересекается с ребром (s, r) другого. Эти полигоны также имеют ориентацию по часовой стрелке, поэтому вы знаете следующую вершину после bи следующая вершина после r, Поскольку края пересекаются, вы удаляете их обоих и добавляете четыре новых. Новые, которые вы добавляете: (a, r), (r, next(b)); (s, b), (b, next(r)), Итак, у вас снова есть два полигона. Это показано на следующем рисунке. Обратите внимание, что при первоначальном удалении только двух ребер (по одному от каждого многоугольника) все пересечения были разрешены.

Ускорение тривиальной реализации O(n^2) на итерацию не совсем легко, и 500 точек на многоугольник - это очень небольшое количество, о котором нужно беспокоиться. Если вы решите, что вам нужно улучшить это время, я бы предложил использовать алгоритм Бентли-Отмана каким-то разумным способом. Интеллектуальный способ заключается в запуске алгоритма, затем, когда вы найдете пересечение, выполните описанную выше процедуру для устранения пересечения, а затем обновите события, которыми руководствуется алгоритм. Надеюсь, что обрабатываемые события могут быть обновлены, не делая алгоритм бесполезным для этой ситуации, но у меня нет доказательств для этого.

Answer 2

Кажется, что вы хотите получить встроенный плоский многоугольник, вершины которого представляют собой именно тот набор точек. Желаемый "порядок" для точек - это то, что вы получите, обойдя границу многоугольника и перечислив вершины в порядке их появления.

Для данного набора точек в общем случае будет более одного встроенного многоугольника с этим свойством; для примера рассмотрим следующий список точек:

(-1,-1), (0,0), (1,0), (1,1), (0,1)

Этот список определяет полигон, отвечающий вашим критериям (если я правильно понимаю). Но так же следующий порядок этого списка:

(-1,-1), (1,0), (0,0), (1,1), (0,1)

Вот один алгоритм, который будет работать (я не знаю о быстром).

Сначала сортируйте ваши точки по x-координате (например, с быстрой сортировкой) в порядке возрастания (назовите этот список L).

Во-вторых, найдите выпуклый корпус (например, с быстрым корпусом); граница выпуклой оболочки будет содержать крайнюю левую и правую точки в отсортированном списке L (назовите их L[1] и L[n]); пусть S - подмножество точек на границе между L[1] и L[n].

Список, который вам нужен, это S в том порядке, в котором он появляется в L (который также будет в том порядке, в котором он появляется на границе выпуклой оболочки), за которым следуют другие элементы LS в обратном порядке, в котором они появляются в L.

Первые две операции обычно должны занимать время O(n log n) (наихудший случай O(n^2)); последнее займет время O(n). Полигон, который вы получите, будет нижней границей выпуклой оболочки (скажем, слева направо) вместе с остальными точками в виде "зигзага" над ними, идущими справа налево.