Построение нескольких радиальных базисных функций нейронной сети на одном графике?

Question

Я хочу построить RBFs Neural Nets на одном графике, например, если они имеют распределение Гаусса. Я попробовал этот код, например:

figure; hold on
N = 3.0;
x=linspace(-N, N);
y=x;
[X,Y]=meshgrid(x,y);
z=(1000/sqrt(2*pi).*exp(-(X.^2/2)-(Y.^2/2)));
surf(X,Y,z);
shading interp
axis tight
N = 3.0;
x=linspace(-N, N);
y=x;
[X,Y]=meshgrid(x,y);
z=(1000/sqrt(2*pi).*exp(-((X-N).^2/2)-((Y-N).^2/2)));
surf(3*X,3*Y,z);
shading interp
axis tight

Но это не заговор, что я ожидаю. Я приложил ожидаемый результат к этому вопросу. Я хочу построить несколько одинаковых RBF с одинаковым распределением Гаусса, но с разными центрами на одном графике. Буду признателен, если вы сможете мне помочь. Также у кого-нибудь есть идея, как построить другой график, также прикрепленный к этому письму, который представляет нечеткие базовые функции.

Базисные функции нейронных сетей:

Нечеткие базисные функции:

Я попытался для второй функции Гаусса теперь с surf(X,Y,z) а также с surf(X-N, Y-N, z) но я все еще вижу только часть сюжета в пределе [-N, N], Я приложил результаты. Первый использует surf(X, Y, z) и второе использование surf(X-N, y-N, z):

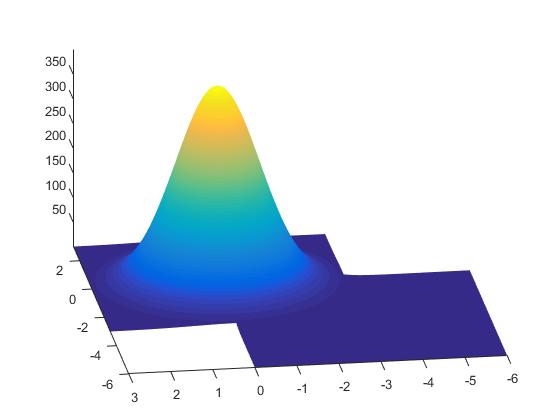
Редактировать 2: Теперь, если я добавлю

xlim([-6 6])
ylim([-6 6])

после команды прибоя это будет результат:

3.jpg

Answer 1

Хорошо, я нашел решение. Вот как это будет решено:

figure; hold on
N = 3.0;
x=linspace(-N, N);
y=x;
[X,Y]=meshgrid(x,y);
z=(500/sqrt(2*pi).*exp(-(X.^2/2)-(Y.^2/2)));
surf(X,Y,z);
shading interp
axis tight

N = 3.0;
x1=linspace(-2*N, 0);
y1=x1;
[X1,Y1]=meshgrid(x1,y1);
z=(500/sqrt(2*pi).*exp(-((X1-N).^2/2)-((Y1-N).^2/2)));
z1=(500/sqrt(2*pi).*exp(-((X1+N).^2/2)-((Y1+N).^2/2)));

surf(X1,Y1,z);
surf(X1,Y1,z1);

xlim([-6 6])
ylim([-6 6])
shading interp
axis tigh

Результат в: 4.jpg