Почему поэлементное сложение намного быстрее в отдельных циклах, чем в комбинированном цикле?
Предполагать a1, b1, c1, а также d1 указать на кучу памяти и мой числовой код имеет следующий основной цикл.
const int n = 100000;
for (int j = 0; j < n; j++) {
a1[j] += b1[j];
c1[j] += d1[j];
}
Этот цикл выполняется 10000 раз через другой внешний for петля. Чтобы ускорить его, я изменил код на:
for (int j = 0; j < n; j++) {
a1[j] += b1[j];
}
for (int j = 0; j < n; j++) {
c1[j] += d1[j];
}
Скомпилированный на MS Visual C++ 10.0 с полной оптимизацией и включенным SSE2 для 32-разрядных на Intel Core 2 Duo (x64), первый пример занимает 5,5 секунды, а пример с двойной петлей - всего 1,9 секунды. Мой вопрос: (Пожалуйста, обратитесь к моему перефразированному вопросу внизу)
PS: я не уверен, если это поможет:
Разборка для первого цикла в основном выглядит следующим образом (этот блок повторяется примерно пять раз в полной программе):
movsd xmm0,mmword ptr [edx+18h]
addsd xmm0,mmword ptr [ecx+20h]
movsd mmword ptr [ecx+20h],xmm0
movsd xmm0,mmword ptr [esi+10h]
addsd xmm0,mmword ptr [eax+30h]
movsd mmword ptr [eax+30h],xmm0
movsd xmm0,mmword ptr [edx+20h]
addsd xmm0,mmword ptr [ecx+28h]
movsd mmword ptr [ecx+28h],xmm0
movsd xmm0,mmword ptr [esi+18h]
addsd xmm0,mmword ptr [eax+38h]
Каждый цикл в примере с двойным циклом создает этот код (следующий блок повторяется примерно три раза):
addsd xmm0,mmword ptr [eax+28h]
movsd mmword ptr [eax+28h],xmm0
movsd xmm0,mmword ptr [ecx+20h]
addsd xmm0,mmword ptr [eax+30h]
movsd mmword ptr [eax+30h],xmm0
movsd xmm0,mmword ptr [ecx+28h]
addsd xmm0,mmword ptr [eax+38h]
movsd mmword ptr [eax+38h],xmm0
movsd xmm0,mmword ptr [ecx+30h]
addsd xmm0,mmword ptr [eax+40h]
movsd mmword ptr [eax+40h],xmm0
Вопрос оказался неактуальным, так как поведение сильно зависит от размеров массивов (n) и кэша ЦП. Так что, если есть дальнейший интерес, я перефразирую вопрос:
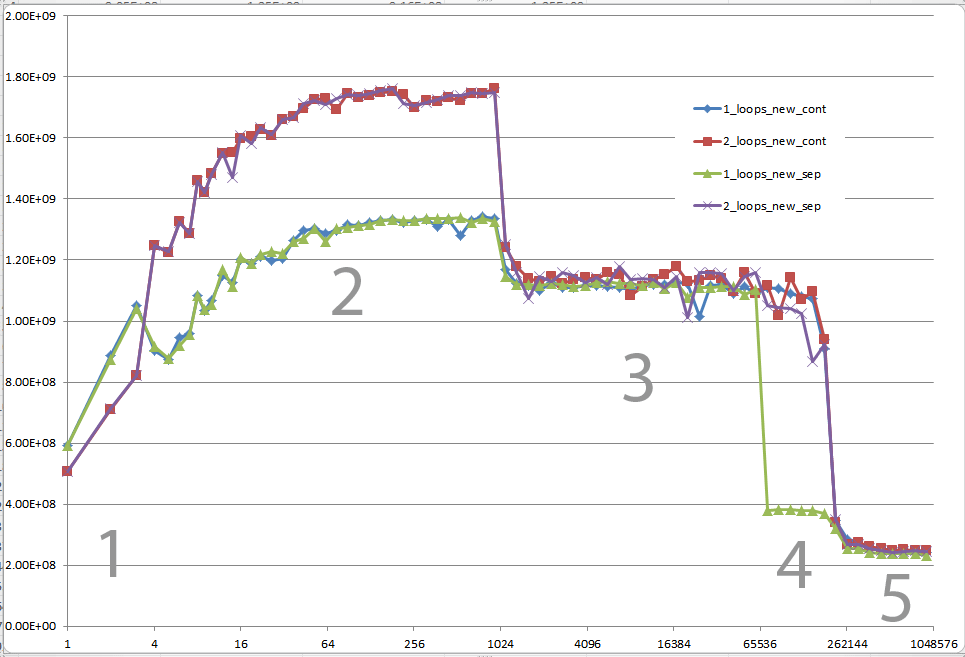
Не могли бы вы дать некоторое подробное представление о деталях, которые приводят к разным поведениям кэша, как показано пятью областями на следующем графике?
Также было бы интересно указать на различия между архитектурами ЦП и кэш-памяти, предоставляя подобный график для этих ЦП.
PPS: вот полный код. Он использует TBB Tick_Count для синхронизации с более высоким разрешением, которую можно отключить, не определяя TBB_TIMING Macro:
#include <iostream>
#include <iomanip>
#include <cmath>
#include <string>
//#define TBB_TIMING
#ifdef TBB_TIMING
#include <tbb/tick_count.h>
using tbb::tick_count;
#else
#include <time.h>
#endif
using namespace std;
//#define preallocate_memory new_cont
enum { new_cont, new_sep };
double *a1, *b1, *c1, *d1;
void allo(int cont, int n)
{
switch(cont) {
case new_cont:
a1 = new double[n*4];
b1 = a1 + n;
c1 = b1 + n;
d1 = c1 + n;
break;
case new_sep:
a1 = new double[n];
b1 = new double[n];
c1 = new double[n];
d1 = new double[n];
break;
}
for (int i = 0; i < n; i++) {
a1[i] = 1.0;
d1[i] = 1.0;
c1[i] = 1.0;
b1[i] = 1.0;
}
}
void ff(int cont)
{
switch(cont){
case new_sep:
delete[] b1;
delete[] c1;
delete[] d1;
case new_cont:
delete[] a1;
}
}
double plain(int n, int m, int cont, int loops)
{
#ifndef preallocate_memory
allo(cont,n);
#endif
#ifdef TBB_TIMING
tick_count t0 = tick_count::now();
#else
clock_t start = clock();
#endif
if (loops == 1) {
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++){
a1[j] += b1[j];
c1[j] += d1[j];
}
}
} else {
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
a1[j] += b1[j];
}
for (int j = 0; j < n; j++) {
c1[j] += d1[j];
}
}
}
double ret;
#ifdef TBB_TIMING
tick_count t1 = tick_count::now();
ret = 2.0*double(n)*double(m)/(t1-t0).seconds();
#else
clock_t end = clock();
ret = 2.0*double(n)*double(m)/(double)(end - start) *double(CLOCKS_PER_SEC);
#endif
#ifndef preallocate_memory
ff(cont);
#endif
return ret;
}
void main()
{
freopen("C:\\test.csv", "w", stdout);
char *s = " ";
string na[2] ={"new_cont", "new_sep"};
cout << "n";
for (int j = 0; j < 2; j++)
for (int i = 1; i <= 2; i++)
#ifdef preallocate_memory
cout << s << i << "_loops_" << na[preallocate_memory];
#else
cout << s << i << "_loops_" << na[j];
#endif
cout << endl;
long long nmax = 1000000;
#ifdef preallocate_memory
allo(preallocate_memory, nmax);
#endif
for (long long n = 1L; n < nmax; n = max(n+1, long long(n*1.2)))
{
const long long m = 10000000/n;
cout << n;
for (int j = 0; j < 2; j++)
for (int i = 1; i <= 2; i++)
cout << s << plain(n, m, j, i);
cout << endl;
}
}
(Показывает FLOP/s для разных значений n.)
11 ответов
После дальнейшего анализа этого, я полагаю, что это (по крайней мере частично) вызвано выравниванием данных четырех указателей. Это приведет к некоторому уровню конфликтов банка / пути кеша.
Если я правильно угадал, как вы размещаете свои массивы, они , скорее всего, будут выровнены по строке страницы.
Это означает, что все ваши обращения в каждом цикле будут попадать в один и тот же путь кеша. Тем не менее, процессоры Intel некоторое время имели 8-стороннюю ассоциативность кэш-памяти L1. Но на самом деле производительность не совсем одинакова. Доступ к 4-сторонним каналам все еще медленнее, чем, скажем, к 2-сторонним.
РЕДАКТИРОВАТЬ: На самом деле это выглядит так, как будто вы распределяете все массивы отдельно. Обычно, когда запрашиваются такие большие выделения, распределитель запрашивает свежие страницы из ОС. Следовательно, существует высокая вероятность того, что большие выделения появятся с тем же смещением от границы страницы.
Вот тестовый код:
int main(){
const int n = 100000;
#ifdef ALLOCATE_SEPERATE
double *a1 = (double*)malloc(n * sizeof(double));
double *b1 = (double*)malloc(n * sizeof(double));
double *c1 = (double*)malloc(n * sizeof(double));
double *d1 = (double*)malloc(n * sizeof(double));
#else
double *a1 = (double*)malloc(n * sizeof(double) * 4);
double *b1 = a1 + n;
double *c1 = b1 + n;
double *d1 = c1 + n;
#endif
// Zero the data to prevent any chance of denormals.
memset(a1,0,n * sizeof(double));
memset(b1,0,n * sizeof(double));
memset(c1,0,n * sizeof(double));
memset(d1,0,n * sizeof(double));
// Print the addresses
cout << a1 << endl;
cout << b1 << endl;
cout << c1 << endl;
cout << d1 << endl;
clock_t start = clock();
int c = 0;
while (c++ < 10000){
#if ONE_LOOP
for(int j=0;j<n;j++){
a1[j] += b1[j];
c1[j] += d1[j];
}
#else
for(int j=0;j<n;j++){
a1[j] += b1[j];
}
for(int j=0;j<n;j++){
c1[j] += d1[j];
}
#endif
}
clock_t end = clock();
cout << "seconds = " << (double)(end - start) / CLOCKS_PER_SEC << endl;
system("pause");
return 0;
}
Результаты тестов:
РЕДАКТИРОВАТЬ: Результаты на компьютере с архитектурой Core 2:
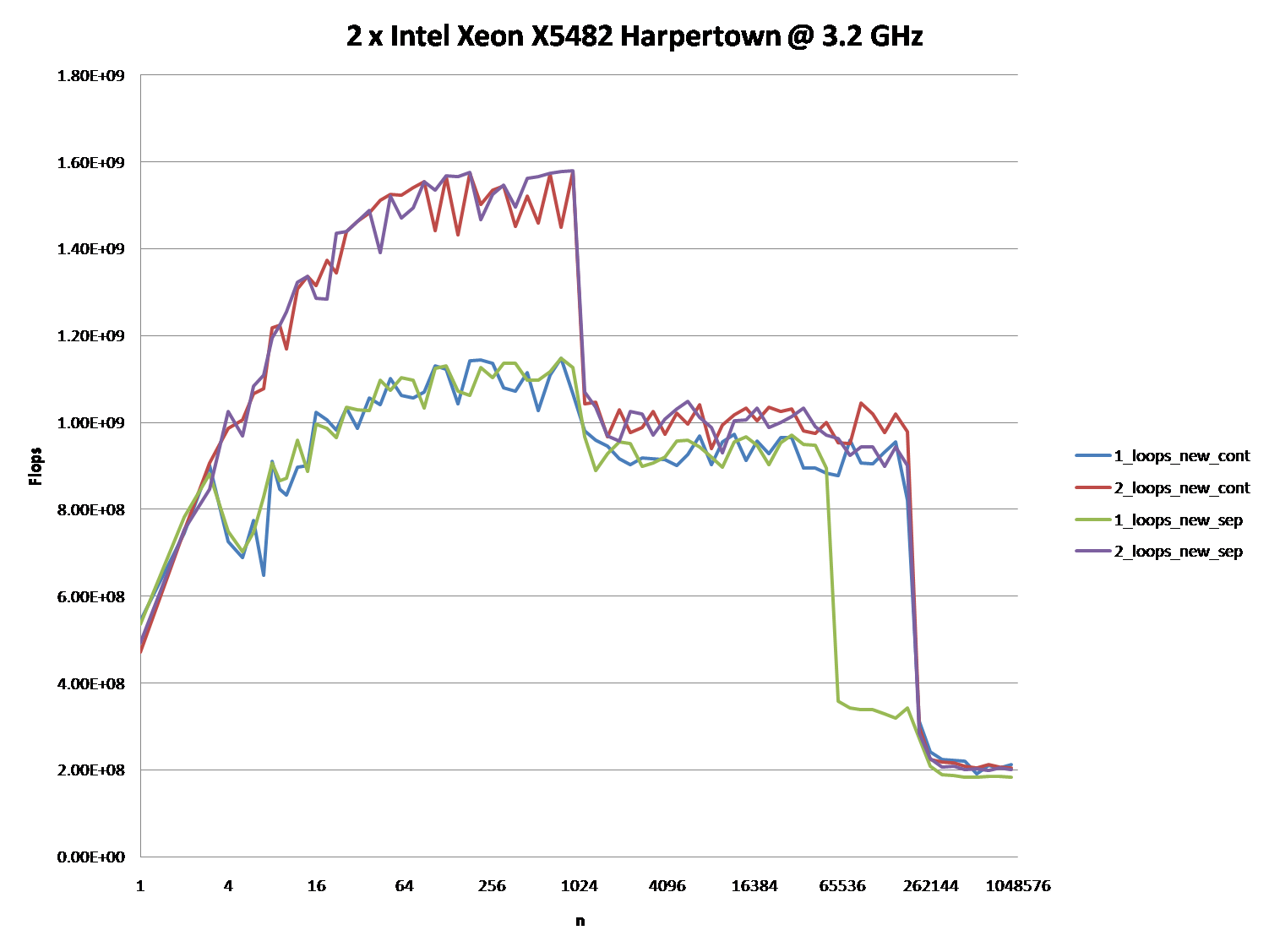
2 x Intel Xeon X5482 Harpertown @ 3,2 ГГц:
#define ALLOCATE_SEPERATE
#define ONE_LOOP
00600020
006D0020
007A0020
00870020
seconds = 6.206
#define ALLOCATE_SEPERATE
//#define ONE_LOOP
005E0020
006B0020
00780020
00850020
seconds = 2.116
//#define ALLOCATE_SEPERATE
#define ONE_LOOP
00570020
00633520
006F6A20
007B9F20
seconds = 1.894
//#define ALLOCATE_SEPERATE
//#define ONE_LOOP
008C0020
00983520
00A46A20
00B09F20
seconds = 1.993
Замечания:
6,206 секунды с одной петлей и2,116 секунды с двумя петлями. Это точно воспроизводит результаты ОП.
В первых двух тестах массивы выделяются отдельно. Вы заметите, что все они имеют одинаковое выравнивание по отношению к странице.
Во вторых двух тестах массивы упакованы вместе, чтобы нарушить это выравнивание. Здесь вы заметите, что обе петли быстрее. Кроме того, второй (двойной) цикл теперь стал медленнее, чем вы обычно ожидаете.
Как отмечает @Stephen Cannon в комментариях, очень вероятно, что это выравнивание приведет кложному наложению псевдонимов в блоках загрузки / хранения или в кеше. Я поиграл по этому поводу и обнаружил, что у Intel на самом деле есть аппаратный счетчик для киосковчастичного адреса:
5 регионов - объяснения
Регион 1:
Это легко. Набор данных настолько мал, что в производительности преобладают издержки, такие как циклы и ветвления.
Регион 2:
Здесь при увеличении размеров данных количество относительных накладных расходов уменьшается, а производительность "насыщается".Здесь два цикла медленнее, потому что он имеет в два раза больше циклов и ветвлений.
Я точно не знаю, что здесь происходит... Выравнивание может сыграть свою роль, поскольку Agner Fog упоминает о конфликтах банков кеша. (Эта ссылка о Sandy Bridge, но идея должна быть применима и к Core 2.)
Регион 3:
На этом этапе данные больше не помещаются в кэш L1. Таким образом, производительность ограничена пропускной способностью кэша L1 <-> L2.
Регион 4:
Мы наблюдаем падение производительности в одном цикле. И, как уже упоминалось, это связано с выравниванием, которое (наиболее вероятно) вызывает ложные смещения псевдонимов в блоках загрузки / хранения процессора.
Однако для того, чтобы произошло ложное наложение, между наборами данных должен быть достаточно большой шаг. Вот почему вы не видите этого в регионе 3.
Регион 5:
На данный момент в кеш ничего не помещается. Таким образом, вы ограничены пропускной способностью памяти.
ОК, правильный ответ определенно должен что-то делать с кешем процессора. Но использовать аргумент кеша довольно сложно, особенно без данных.
Есть много ответов, которые привели к большому обсуждению, но давайте посмотрим правде в глаза: проблемы с кэшем могут быть очень сложными и не одномерными. Они сильно зависят от размера данных, поэтому мой вопрос был несправедливым: он оказался в очень интересном месте на графике кеша.
Ответ @Mysticial убедил многих людей (в том числе и меня), вероятно, потому, что он был единственным, кто, казалось, полагался на факты, но это была только одна "точка данных" правды.
Вот почему я объединил его тест (используя непрерывное или раздельное распределение) и совет Ответа @James.
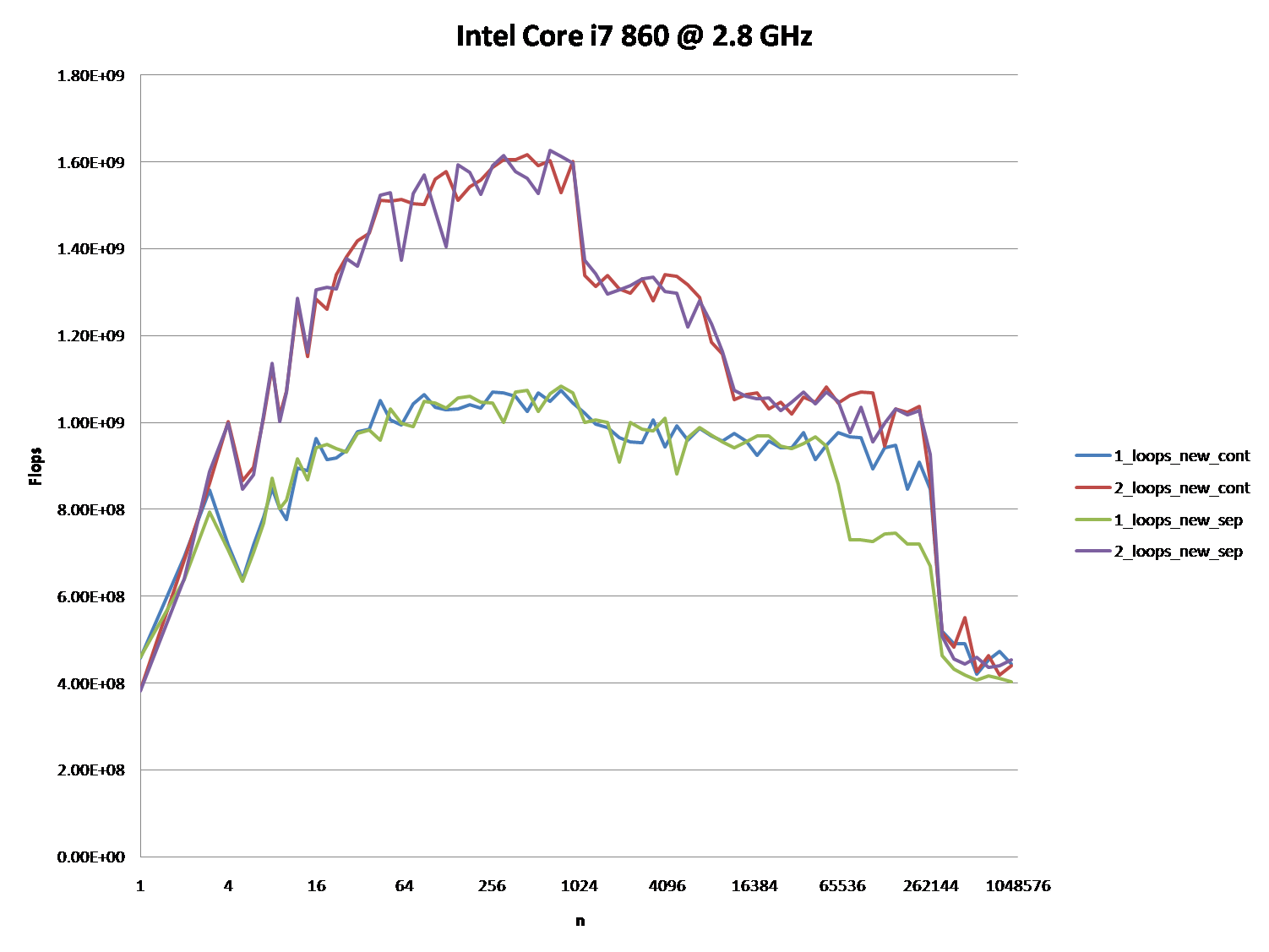
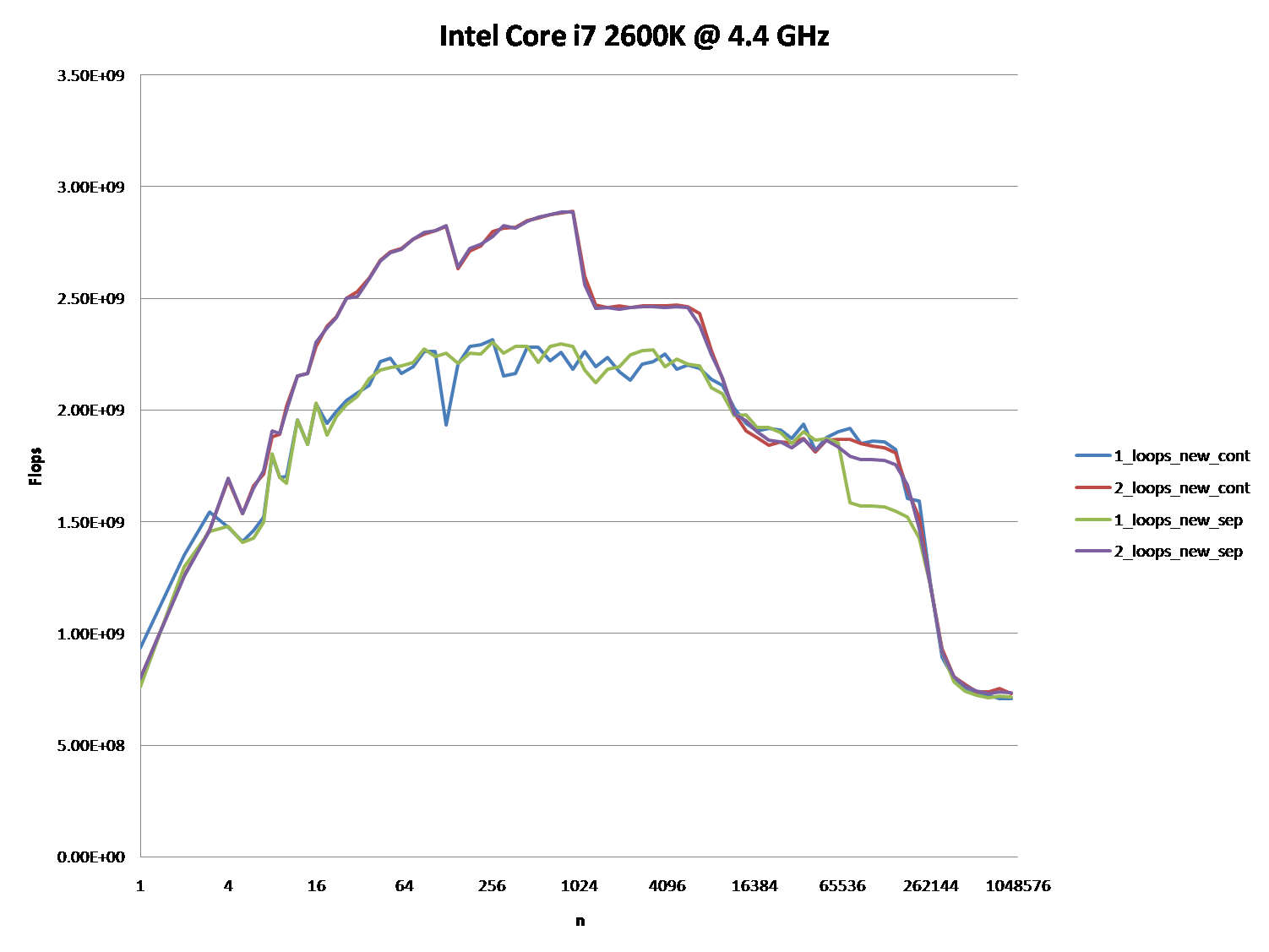
Приведенные ниже графики показывают, что большинство ответов и особенно большинство комментариев к вопросу и ответам можно считать совершенно неправильными или верными в зависимости от конкретного сценария и используемых параметров.
Обратите внимание, что мой первоначальный вопрос был при n = 100.000. Эта точка (случайно) демонстрирует особое поведение:
Он обладает наибольшим расхождением между версией с одним и двумя циклами (почти в три раза)
Это единственная точка, где однопетлевая (а именно с непрерывным распределением) превосходит двухконтурную версию. (Это сделало возможным ответ Mysticial.)
Результат с использованием инициализированных данных:
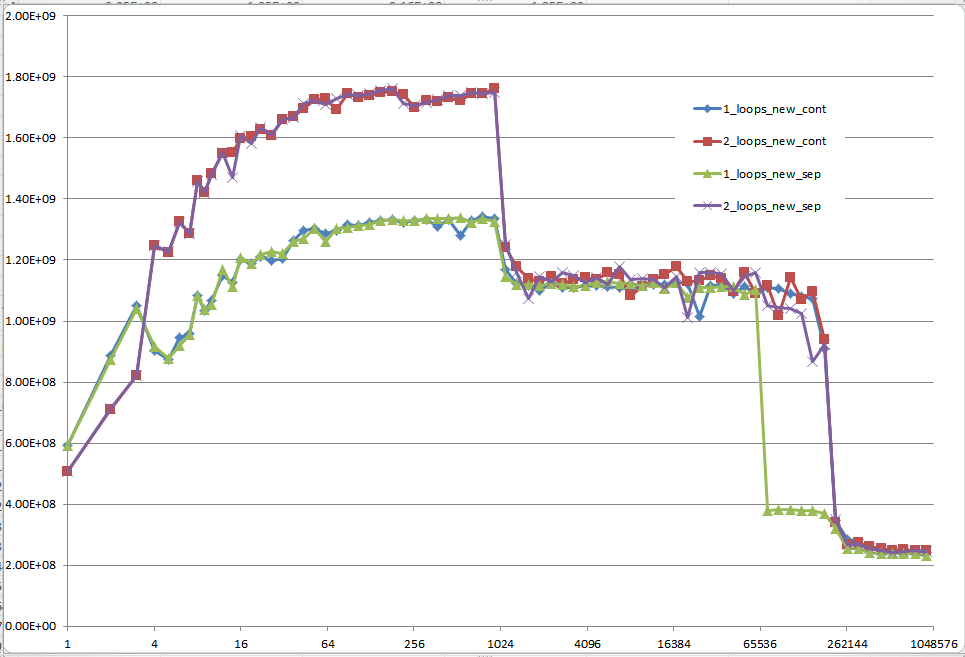
Результат с использованием неинициализированных данных (это то, что проверил Mysticial):
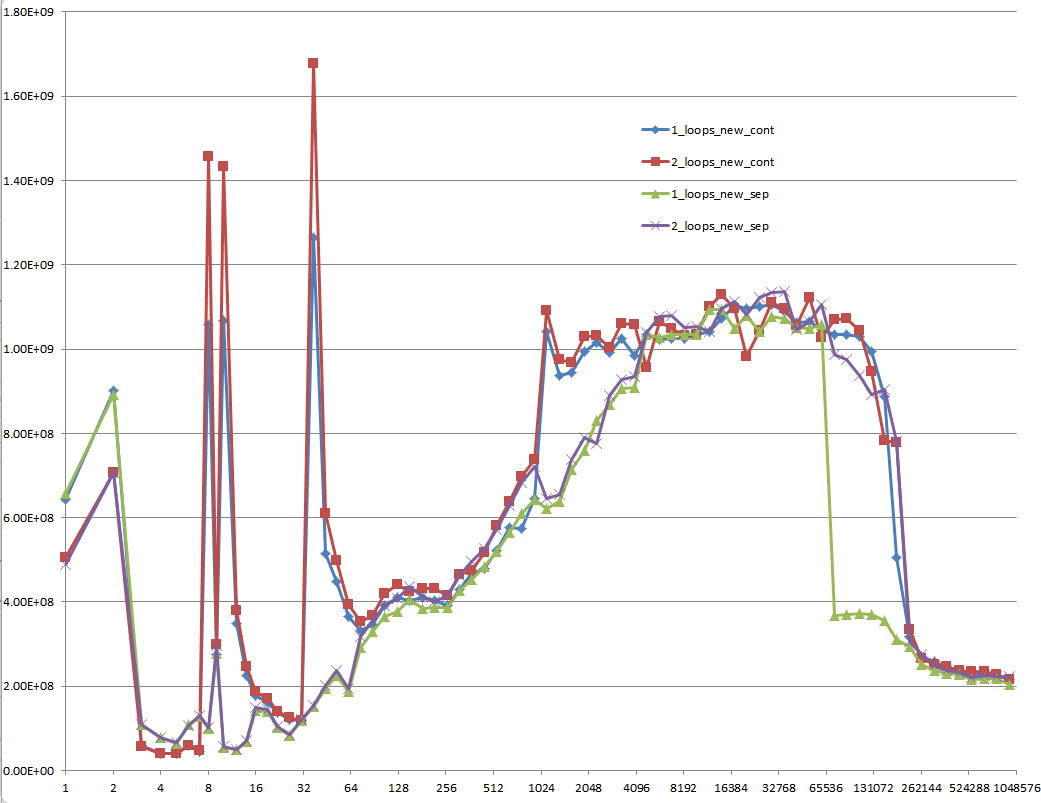
И это трудно объяснить: инициализированные данные, которые выделяются один раз и используются повторно для каждого следующего теста с разным размером вектора:
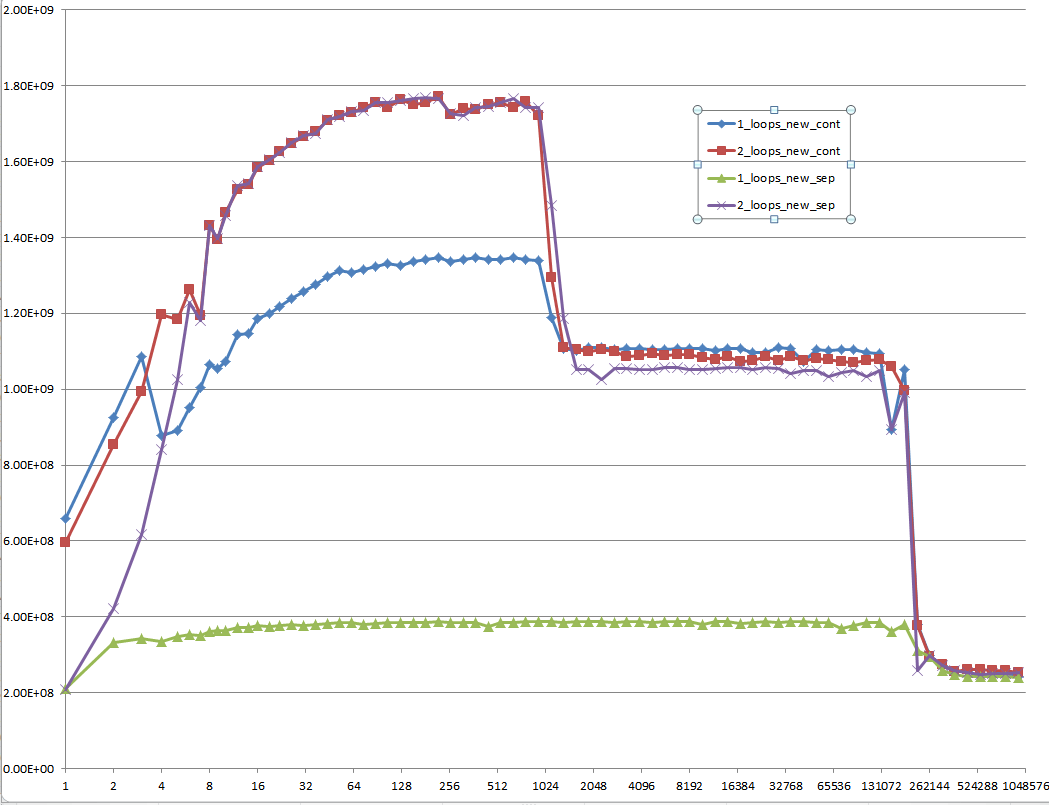
Предложение
Каждый вопрос низкого уровня производительности, касающийся переполнения стека, должен требовать предоставления информации MFLOPS для всего диапазона размеров данных, связанных с кэшем! Это пустая трата времени на то, чтобы думать об ответах и особенно обсуждать их с другими без этой информации.
Второй цикл включает в себя гораздо меньшую активность кеша, поэтому процессору легче справляться с требованиями к памяти.
Представьте, что вы работаете на машине, где n это было просто правильное значение для того, чтобы иметь возможность хранить два ваших массива в памяти одновременно, но общего объема доступной памяти посредством кэширования на диске все еще было достаточно для хранения всех четырех.
Предполагая простую политику кэширования LIFO, этот код:
for(int j=0;j<n;j++){
a[j] += b[j];
}
for(int j=0;j<n;j++){
c[j] += d[j];
}
будет в первую очередь вызвать a а также b быть загруженным в ОЗУ, а затем работать полностью в ОЗУ. Когда начинается второй цикл, c а также d затем будет загружен с диска в оперативную память и запущен.
другой цикл
for(int j=0;j<n;j++){
a[j] += b[j];
c[j] += d[j];
}
будет выводить два массива и страницу в двух других каждый раз вокруг цикла. Это, очевидно, будет намного медленнее.
Вы, вероятно, не видите кеширование диска в своих тестах, но вы, вероятно, видите побочные эффекты какой-либо другой формы кеширования.
Кажется, здесь есть небольшая путаница / недоразумение, поэтому я попытаюсь немного уточнить на примере.
Сказать n = 2 и мы работаем с байтами. Таким образом, в моем сценарии у нас всего 4 байта оперативной памяти, а остальная часть памяти значительно медленнее (скажем, в 100 раз больше доступа).
Предполагая довольно глупую политику кеширования, если байт не находится в кеше, поместите его туда и получите следующий байт, пока мы на нем, вы получите сценарий примерно такой:
С
for(int j=0;j<n;j++){ a[j] += b[j]; } for(int j=0;j<n;j++){ c[j] += d[j]; }кэш
a[0]а такжеa[1]затемb[0]а такжеb[1]и установитьa[0] = a[0] + b[0]в кеше - теперь в кеше четыре байта,a[0], a[1]а такжеb[0], b[1], Стоимость = 100 + 100.- задавать
a[1] = a[1] + b[1]в кеше Стоимость = 1 + 1. - Повторите для
cа такжеd, Общая стоимость =
(100 + 100 + 1 + 1) * 2 = 404С
for(int j=0;j<n;j++){ a[j] += b[j]; c[j] += d[j]; }кэш
a[0]а такжеa[1]затемb[0]а такжеb[1]и установитьa[0] = a[0] + b[0]в кеше - теперь в кеше четыре байта,a[0], a[1]а такжеb[0], b[1], Стоимость = 100 + 100.- выталкивать
a[0], a[1], b[0], b[1]из кеша и кешаc[0]а такжеc[1]затемd[0]а такжеd[1]и установитьc[0] = c[0] + d[0]в кеше Стоимость = 100 + 100. - Я подозреваю, что вы начинаете видеть, куда я иду.
- Общая стоимость =
(100 + 100 + 100 + 100) * 2 = 800
Это классический сценарий трэша кеша.
Это не из-за другого кода, а из-за кеширования: ОЗУ медленнее, чем регистры ЦП, а кэш-память находится внутри ЦП, чтобы избежать записи в ОЗУ каждый раз, когда переменная изменяется. Но кэш не такой большой, как оперативная память, следовательно, он отображает только ее часть.
Первый код изменяет адреса удаленной памяти, чередуя их в каждом цикле, таким образом, постоянно требуя аннулировать кэш.
Второй код не чередуется: он просто передается по соседним адресам дважды. Это заставляет всю работу завершаться в кэше, аннулируя ее только после запуска второго цикла.
Я не могу повторить результаты, обсуждаемые здесь.
Я не знаю, виноват ли плохой тестовый код, или что, но эти два метода находятся в пределах 10% друг от друга на моей машине, используя следующий код, и один цикл обычно немного быстрее, чем два - как вы ожидать.
Размеры массивов варьировались от 2^16 до 2^24 с использованием восьми циклов. Я был осторожен, чтобы инициализировать исходные массивы, чтобы += задание не просило FPU добавить мусор памяти, интерпретируемый как double.
Я играл с различными схемами, такими как сдача задания b[j], d[j] в InitToZero[j] внутри петель, а также с использованием += b[j] = 1 а также += d[j] = 1и я получил довольно последовательные результаты.
Как и следовало ожидать, инициализация b а также d внутри цикла, используя InitToZero[j] дал комбинированный подход преимущество, так как они были сделаны вплотную перед заданиями a а также c, но все же в пределах 10%. Пойди разберись.
Аппаратное обеспечение - Dell XPS 8500 с процессором 3 Core i7 @ 3,4 ГГц и 8 ГБ памяти. Для 2^16 до 2^24, используя восемь циклов, совокупное время было 44,987 и 40,965 соответственно. Visual C++ 2010, полностью оптимизирован.
PS: я изменил циклы для обратного отсчета до нуля, и комбинированный метод был немного быстрее. Почесывая голову Обратите внимание на новый размер массива и количество циклов.
// MemBufferMystery.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
#include <iostream>
#include <cmath>
#include <string>
#include <time.h>
#define dbl double
#define MAX_ARRAY_SZ 262145 //16777216 // AKA (2^24)
#define STEP_SZ 1024 // 65536 // AKA (2^16)
int _tmain(int argc, _TCHAR* argv[]) {
long i, j, ArraySz = 0, LoopKnt = 1024;
time_t start, Cumulative_Combined = 0, Cumulative_Separate = 0;
dbl *a = NULL, *b = NULL, *c = NULL, *d = NULL, *InitToOnes = NULL;
a = (dbl *)calloc( MAX_ARRAY_SZ, sizeof(dbl));
b = (dbl *)calloc( MAX_ARRAY_SZ, sizeof(dbl));
c = (dbl *)calloc( MAX_ARRAY_SZ, sizeof(dbl));
d = (dbl *)calloc( MAX_ARRAY_SZ, sizeof(dbl));
InitToOnes = (dbl *)calloc( MAX_ARRAY_SZ, sizeof(dbl));
// Initialize array to 1.0 second.
for(j = 0; j< MAX_ARRAY_SZ; j++) {
InitToOnes[j] = 1.0;
}
// Increase size of arrays and time
for(ArraySz = STEP_SZ; ArraySz<MAX_ARRAY_SZ; ArraySz += STEP_SZ) {
a = (dbl *)realloc(a, ArraySz * sizeof(dbl));
b = (dbl *)realloc(b, ArraySz * sizeof(dbl));
c = (dbl *)realloc(c, ArraySz * sizeof(dbl));
d = (dbl *)realloc(d, ArraySz * sizeof(dbl));
// Outside the timing loop, initialize
// b and d arrays to 1.0 sec for consistent += performance.
memcpy((void *)b, (void *)InitToOnes, ArraySz * sizeof(dbl));
memcpy((void *)d, (void *)InitToOnes, ArraySz * sizeof(dbl));
start = clock();
for(i = LoopKnt; i; i--) {
for(j = ArraySz; j; j--) {
a[j] += b[j];
c[j] += d[j];
}
}
Cumulative_Combined += (clock()-start);
printf("\n %6i miliseconds for combined array sizes %i and %i loops",
(int)(clock()-start), ArraySz, LoopKnt);
start = clock();
for(i = LoopKnt; i; i--) {
for(j = ArraySz; j; j--) {
a[j] += b[j];
}
for(j = ArraySz; j; j--) {
c[j] += d[j];
}
}
Cumulative_Separate += (clock()-start);
printf("\n %6i miliseconds for separate array sizes %i and %i loops \n",
(int)(clock()-start), ArraySz, LoopKnt);
}
printf("\n Cumulative combined array processing took %10.3f seconds",
(dbl)(Cumulative_Combined/(dbl)CLOCKS_PER_SEC));
printf("\n Cumulative seperate array processing took %10.3f seconds",
(dbl)(Cumulative_Separate/(dbl)CLOCKS_PER_SEC));
getchar();
free(a); free(b); free(c); free(d); free(InitToOnes);
return 0;
}
Я не уверен, почему было решено, что MFLOPS был релевантным показателем. Хотя идея заключалась в том, чтобы сосредоточиться на доступе к памяти, поэтому я попытался минимизировать время вычислений с плавающей запятой. Я оставил в +=, но я не уверен почему.
Прямое назначение без вычислений было бы более точным тестом времени доступа к памяти и создало бы тест, который был бы равномерным независимо от числа циклов. Может быть, я что-то упустил в разговоре, но об этом стоит подумать дважды. Если плюс не входит в задание, совокупное время почти одинаково и составляет 31 секунда.
Это связано с тем, что в процессоре не так много промахов кэша (когда ему приходится ждать получения данных массива из микросхем ОЗУ). Было бы интересно непрерывно корректировать размер массивов, чтобы вы превышали размеры кэша 1-го уровня (L1), а затем кэша 2-го уровня (L2) вашего ЦП и отображали время, необходимое для вашего кода. выполнить по размерам массивов. График не должен быть прямой линией, как вы ожидаете.
Первый цикл чередует запись в каждой переменной. Второй и третий только делают небольшие скачки размера элемента.
Попробуйте написать две параллельные линии по 20 крестиков с помощью ручки и бумаги, разделенных на 20 см. Попробуйте один раз закончить одну, а затем другую строку и попробуйте другой раз, поочередно записывая крестик в каждой строке.
Оригинальный вопрос
Почему один цикл намного медленнее двух?
Заключение:
Случай 1 - это классическая проблема интерполяции, которая оказывается неэффективной. Я также думаю, что это было одной из главных причин того, почему многие машинные архитектуры и разработчики закончили создавать и проектировать многоядерные системы с возможностью выполнения многопоточных приложений, а также параллельного программирования.
Рассматривая это с помощью такого подхода, не затрагивая, как аппаратное обеспечение, ОС и компилятор (-ы) работают вместе для выделения кучи, которая включает в себя работу с ОЗУ, кэш-памятью, файлами подкачки и т. Д.; математика, лежащая в основе этих алгоритмов, показывает нам, какой из этих двух вариантов является лучшим решением. Мы можем использовать аналогию, где Boss или же Summation это будет представлять For Loop который должен путешествовать между рабочими A & B мы можем легко видеть, что Случай 2 по крайней мере на 1/2 быстрее, если не чуть больше, чемСлучай 1 из-за разницы в расстоянии, необходимом для перемещения, и времени, затрачиваемом между работниками. Эта математика почти виртуально и идеально соответствует как Bench Mark Times, так и разнице в инструкциях по сборке.
Теперь я начну объяснять, как все это работает ниже.
Оценивая проблему
Код ОП:
const int n=100000;
for(int j=0;j<n;j++){
a1[j] += b1[j];
c1[j] += d1[j];
}
А также
for(int j=0;j<n;j++){
a1[j] += b1[j];
}
for(int j=0;j<n;j++){
c1[j] += d1[j];
}
Рассмотрение
Рассматривая оригинальный вопрос ОП о двух вариантах циклов for и его исправленный вопрос о поведении кэшей, а также множество других превосходных ответов и полезных комментариев; Я хотел бы попытаться сделать что-то другое здесь, используя другой подход к этой ситуации и проблеме.
Подход
Учитывая два цикла и все дискуссии о кешировании и хранении страниц, я бы хотел использовать другой подход, чтобы взглянуть на это с другой точки зрения. Тот, который не включает кеш и файлы подкачки, ни выполнения для выделения памяти, на самом деле этот подход вообще не касается реального оборудования или программного обеспечения.
Перспектива
Посмотрев некоторое время на код, стало совершенно очевидно, в чем проблема и что ее генерирует. Давайте разберем это в алгоритмической задаче и рассмотрим ее с точки зрения использования математических обозначений, а затем применим аналогию к математическим задачам, а также к алгоритмам.
Что мы знаем
Мы знаем, что его цикл будет выполняться 100000 раз. Мы также знаем, чтоa1,b1, c1& d1являются указателями на 64-битную архитектуру. В C++ на 32-разрядной машине все указатели имеют размер 4 байта, а на 64-разрядной машине они имеют размер 8 байтов, поскольку указатели имеют фиксированную длину. Мы знаем, что у нас есть 32 байта для выделения в обоих случаях. Единственное отличие состоит в том, что мы выделяем 32 байта или 2 набора по 2-8 байт на каждую итерацию, тогда как во 2-м случае мы выделяем 16 байтов для каждой итерации для обоих независимых циклов. Таким образом, оба цикла по-прежнему равны 32 байта в общем распределении. С этой информацией давайте продолжим и покажем общую математику, алгоритм и аналогию. Мы знаем, сколько раз один и тот же набор или группа операций должны быть выполнены в обоих случаях. Мы знаем объем памяти, который должен быть выделен в обоих случаях. Мы можем оценить, что общая рабочая нагрузка распределений между обоими случаями будет примерно одинаковой.
Что мы не знаем
Мы не знаем, сколько времени это займет для каждого случая, если только мы не установим счетчик и не проведем тест. Однако контрольные показатели уже были включены в исходный вопрос, а также в некоторые ответы и комментарии, и мы можем видеть существенную разницу между этими двумя вопросами, и в этом заключается полное обоснование этого вопроса для этой проблемы и для ответа на него в начинается с.
Давайте расследовать
Уже очевидно, что многие уже сделали это, взглянув на распределение кучи, тесты производительности, на RAM, Cache и Page Files. Рассмотрение конкретных точек данных и конкретных итерационных индексов также было включено, и различные разговоры об этой конкретной проблеме заставили многих людей начать сомневаться в других связанных с этим вещах. Итак, как нам начать смотреть на эту проблему, используя математические алгоритмы и применяя к ней аналогию? Начнем с того, что сделаем пару утверждений! Затем мы строим наш алгоритм оттуда.
Наши утверждения:
- Мы позволим нашему циклу и его итерациям быть суммированием, которое начинается с 1 и заканчивается на 100000 вместо того, чтобы начинаться с 0, как в циклах, поскольку нам не нужно беспокоиться о схеме индексации адресации памяти 0, так как нас просто интересует сам алгоритм.
- В обоих случаях у нас есть 4 функции для работы и 2 вызова функций с 2 операциями, выполняемыми для каждого вызова функции. Таким образом, мы установим их как функции и вызовы функций, чтобы
F1(),F2(),f(a),f(b),f(c)а такжеf(d),
Алгоритмы:
1-й случай:- только одно суммирование, но два независимых вызова функций.
Sum n=1 : [1,100000] = F1(), F2();
F1() = { f(a) = f(a) + f(b); }
F2() = { f(c) = f(c) + f(d); }
2-й случай:- Два суммирования, но у каждого свой вызов функции.
Sum1 n=1 : [1,100000] = F1();
F1() = { f(a) = f(a) + f(b); }
Sum2 n=1 : [1,100000] = F1();
F1() = { f(c) = f(c) + f(d); }
Если вы заметилиF2()существует только вSumгде оба Sum1 а также Sum2 только содержит F1(), Это также станет очевидным позже, когда мы начнем делать вывод, что со вторым алгоритмом происходит своего рода оптимизация.
Итерации по первому случаюSumзвонкиf(a)что добавит к себе f(b) тогда это вызывает f(c) это будет делать то же самое, но добавить f(d) себе для каждого 100000 iterations, Во втором случае мы имеем Sum1 а также Sum2И оба действуют одинаково, как если бы они были одной и той же функцией, вызываемой дважды подряд. В этом случае мы можем лечить Sum1 а также Sum2 просто старый Sum где Sum в этом случае выглядит так: Sum n=1 : [1,100000] { f(a) = f(a) + f(b); } и теперь это выглядит как оптимизация, где мы можем просто считать, что это та же самая функция.
Резюме с аналогией
С тем, что мы видели во втором случае, это выглядит почти так, как будто есть оптимизация, так как оба цикла имеют одинаковую точную сигнатуру, но это не настоящая проблема. Проблема не в работе, которая выполняетсяf(a),f(b), f(c)&f(d)в обоих случаях и при сравнении между ними разница в расстоянии, которую должно пройти суммирование в обоих случаях, дает вам разницу во времени выполнения.
Думать оFor Loopsкак являющийсяSummationsчто делает итерации как Boss то есть приказывает двум людям A & B и что их работа на мясо C & D соответственно и забрать у них посылку и вернуть. По аналогии здесь итерации цикла или суммирования и проверки самих условий на самом деле не представляют Boss, Что на самом деле представляет Boss здесь не из фактических математических алгоритмов напрямую, но из фактической концепции Scopeа также Code Block внутри подпрограммы или подпрограммы, метода, функции, единицы перевода и т. д. Первый алгоритм имеет 1 область действия, где 2-й алгоритм имеет 2 последовательных области действия.
В первом случае при каждом вызове Bossидет кAи дает заказ и A уходит, чтобы получить B's пакет тогда Boss идет к C и дает приказы сделать то же самое и получить посылку от D на каждой итерации.
Во втором случаеBossработает напрямую сAпойти и принести B's пакет, пока все пакеты не будут получены. Тогда Boss работает с C сделать то же самое для получения всех D's пакеты.
Поскольку мы работаем с 8-байтовым указателем и занимаемся распределением кучи, давайте рассмотрим эту проблему здесь. Допустим, что Bossв 100 футах отAи это A 500 футов от C, Нам не нужно беспокоиться о том, как далеко Boss изначально из Cиз-за порядка казней. В обоих случаях Boss изначально путешествует из A сначала потом B, Эта аналогия не говорит о том, что это расстояние является точным; это всего лишь сценарий использования теста, чтобы показать работу алгоритмов. Во многих случаях при распределении кучи и работе с кешем и файлами подкачки эти расстояния между адресами могут не сильно различаться или могут очень сильно зависеть от характера типов данных и размеров массива.
Тестовые случаи:
Первый случай: на первой итерацииBossдолжен сначала пройти 100 футов, чтобы сдать ордерA а также A уходит и делает свое дело, но тогда Boss должен пройти 500 футов до C отдать ему свой заказ. Затем на следующей итерации и на каждой другой итерации после Boss должен идти вперед и назад 500 футов между двумя.
Второй случай:The Bossдолжен пройти 100 футов на первой итерацииA, но после этого он уже там и просто ждетA чтобы вернуться, пока не заполнены все промахи. Тогда Bossдолжен пройти 500 футов на первой итерации C так как C 500 футов от A с этого Boss( Summation, For Loop ) вызывается сразу после работы с A а потом просто ждет, как он сделал с A пока все C's заказ бланки сделаны.
Разница в пройденных расстояниях
const n = 100000
distTraveledOfFirst = (100 + 500) + ((n-1)*(500 + 500);
// Simplify
distTraveledOfFirst = 600 + (99999*100);
distTraveledOfFirst = 600 + 9999900;
distTraveledOfFirst = 10000500;
// Distance Traveled On First Algorithm = 10,000,500ft
distTraveledOfSecond = 100 + 500 = 600;
// Distance Traveled On Second Algorithm = 600ft;
Сравнение произвольных значений
Мы легко видим, что 600 - это гораздо меньше, чем 10 миллионов. Теперь это не точно, потому что мы не знаем фактической разницы в расстоянии между тем, какой адрес ОЗУ или из какого Cache или файла подкачки каждый вызов на каждой итерации будет вызван многими другими невидимыми переменными, но это просто оценка ситуации, которую нужно знать, и попытка взглянуть на нее с наихудшего сценария.
Таким образом, по этим числам это будет выглядеть так, как будто Алгоритм Один должен быть на 99% медленнее, чем Алгоритм Два; тем не менее, это только The Boss'sчасть или ответственность алгоритмов, и это не учитывает фактических работниковA, B, C& Dи что они должны делать на каждой итерации цикла. Таким образом, работа боссов составляет только около 15 - 40% всей выполняемой работы. Таким образом, основная часть работы, выполняемой рабочими, оказывает чуть большее влияние на поддержание соотношения разности скоростей примерно до 50-70%.
Наблюдение:-Различия между двумя алгоритмами
В этой ситуации это структура процесса выполняемой работы, и он показывает, чтовариант 2 более эффективен как при частичной оптимизации, так и при наличии аналогичного объявления функции и определения, где только переменные различаются по имени., И мы также видим, что общее расстояние, пройденное в случае 1, намного больше, чем в случае 2, и мы можем считать это расстояние пройденным нашим Фактором времени между двумя алгоритмами. Дело 1 требует гораздо больше работы, чем дело 2. Это также было видно в свидетельстве ASMэто было показано между обоими случаями. Даже с учетом того, что уже было сказано об этих случаях, это также не учитывает тот факт, что вслучае 1 босс должен ждать обоих A&C чтобы вернуться, прежде чем он сможет вернуться к A снова на следующей итерации, и это также не учитывает тот факт, что если A или же B занимает очень много времени, то оба Boss и другие работники также ожидают простоя. В случае 2 бездействует только Bossпока работник не вернется. Так что даже это влияет на алгоритм.
Измененные вопросы ОП
РЕДАКТИРОВАТЬ: Вопрос оказался неактуальным, так как поведение сильно зависит от размеров массивов (n) и кэш-памяти ЦП. Так что, если есть дальнейший интерес, я перефразирую вопрос:
Не могли бы вы дать некоторое подробное представление о деталях, которые приводят к разным поведениям кэша, как показано пятью областями на следующем графике?
Также было бы интересно указать на различия между архитектурами ЦП и кэш-памяти, предоставляя подобный график для этих ЦП.
Относительно этих вопросов
Без сомнения, я продемонстрировал, что существует проблема, лежащая в основе еще до того, как аппаратное и программное обеспечение подключается. Теперь что касается управления памятью и кэшированием вместе с файлами подкачки и т. Д., Которые все работают вместе в интегрированном наборе систем между: The Architecture {Аппаратное обеспечение, прошивка, некоторые встроенные драйверы, ядра и наборы инструкций ASM}, The OS{Системы управления файлами и памятью, драйверы и реестр}, The Compiler {Единицы перевода и оптимизации исходного кода}, и даже Source Code сам с его набором (-ами) отличительных алгоритмов; мы уже можем видеть, что существует узкое место, которое происходит в первом алгоритме, прежде чем мы даже применим его к любой машине с любым произвольным Architecture, OS, а также Programmable Language по сравнению со вторым алгоритмом. Таким образом, уже существовала проблема, прежде чем задействовать внутренние особенности современного компьютера.
Конечные результаты
Тем не мение; Нельзя сказать, что эти новые вопросы не важны, потому что они сами по себе и играют роль в конце концов. Они действительно влияют на процедуры и общую эффективность, и это видно из различных графиков и оценок от многих, которые дали свои ответы и / или комментарии. Если обратить внимание на аналогию Boss и двое рабочих A & B кто должен был пойти и получить пакеты от C & D соответственно и рассматривая математические обозначения этих двух алгоритмов, вы можете видеть, что даже без участия компьютера Case 2 примерно на 60% быстрее, чем Case 1 и когда вы смотрите на графики и диаграммы после того, как эти алгоритмы были применены к исходному коду, скомпилированы и оптимизированы и выполнены с помощью ОС для выполнения операций на данном оборудовании, вы даже увидите немного большее снижение различий в этих алгоритмах.
Теперь, если набор "данных" довольно мал, на первый взгляд может показаться, что разница не такая уж плохая Case 1 около 60 - 70% медленнее чем Case 2 мы можем посмотреть на рост этой функции как на разницу во времени выполнения:
DeltaTimeDifference approximately = Loop1(time) - Loop2(time)
//where
Loop1(time) = Loop2(time) + (Loop2(time)*[0.6,0.7]) // approximately
// So when we substitute this back into the difference equation we end up with
DeltaTimeDifference approximately = (Loop2(time) + (Loop2(time)*[0.6,0.7])) - Loop2(time)
// And finally we can simplify this to
DeltaTimeDifference approximately = [0.6,0.7]*(Loop2(time)
И это приближение является средней разницей между этими двумя циклами как алгоритмически, так и машинными операциями, включающими оптимизацию программного обеспечения и машинные инструкции. Поэтому, когда набор данных растет линейно, увеличивается и разница во времени между ними. Алгоритм 1 имеет больше выборок, чем алгоритм 2, что очевидно, когда Boss пришлось путешествовать туда и обратно на максимальное расстояние между A & C для каждой итерации после первой итерации, в то время как алгоритм 2 Boss пришлось ехать в A один раз и потом, сделав A он должен был проехать максимальное расстояние только один раз, когда A в C,
Так что пытаясь иметь Boss сосредоточение на выполнении двух одинаковых вещей одновременно и жонглирование ими взад и вперед вместо того, чтобы концентрироваться на похожих последовательных задачах, к концу дня заставит его сильно рассердиться, потому что он должен был путешествовать и работать вдвое больше. Поэтому не теряйте масштаб ситуации, позволяя вашему боссу попасть в интерполированное узкое место, потому что супруга и дети босса этого не оценят.
Это может быть старый C++ и оптимизации. На моем компьютере я получил почти такую же скорость:
Один цикл: 1,577 мс
Два цикла: 1,507 мс
Я использую Visual Studio 2015 на процессоре E5-1620 с частотой 3,5 ГГц и 16 ГБ ОЗУ.
Чтобы этот код выполнялся быстро, процессору потребуется выполнить предварительную выборку из кэша. По сути, ЦП узнает, что вы получаете доступ к последовательным данным, и считывает данные из ОЗУ до того, как они действительно понадобятся.
Двойной цикл имеет два входных и два выходных потока, поэтому для быстрой работы требуется четыре отдельных операции предварительной выборки. Вторым циклам нужны только две отдельные операции предварительной выборки. Если вы запустите этот код на процессоре, который может автоматически выбирать две, но не четыре строки кэша, первая версия будет медленнее.
На улучшенном процессоре проблема исчезнет. В этом случае вы можете изменить код, добавив три массива к четвертому, и, вероятно, более мощный процессор сможет выполнить предварительную выборку 4, но не восьми потоков и покажет тот же эффект.