Вороной Тесселяция в Python

Question

Проблема с назначением узла

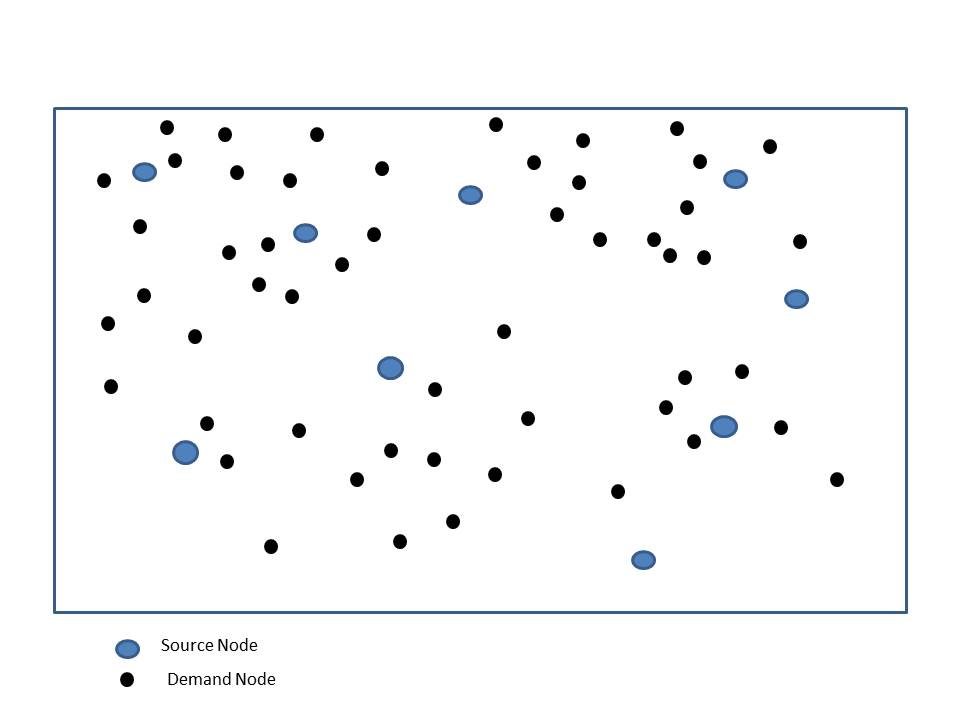
Проблема, которую я хочу решить, состоит в том, чтобы создать тесселяцию карты, заданной синими узлами (исходными узлами) в качестве заданных входных точек. После того, как я смогу это сделать, я хотел бы увидеть, сколько черных узлов (узлов спроса) попадает в каждую ячейку, и назначьте его Синему Узлу, связанному с этой ячейкой.

Я хотел бы знать, есть ли более простой способ сделать это без использования алгоритма Fortune. Я столкнулся с этой функцией в Mahotas, которая называется Mahotas.segmentation.gvoronoi (image) source. Но я не уверен, что это решит мою проблему.

Также, пожалуйста, предложите мне, если есть лучший способ сделать эту сегментацию (кроме тесселяции Вороного). Я не уверен, что алгоритмы кластеризации будут хорошим выбором. Я новичок в программировании.

Answer 1

Вот альтернативный подход к использованию тесселяции Вороного:

Постройте дерево kd поверх исходных узлов. Затем для каждого узла спроса используйте дерево kd, чтобы найти ближайший узел источника и увеличить счетчик, связанный с этим соседним узлом источника.

Реализация дерева kd, найденного по адресу http://code.google.com/p/python-kdtree/ должна быть полезной.

Answer 2

Я просто искал то же самое и нашел это:

https://github.com/Softbass/py_geo_voronoi

Answer 3

На вашей диаграмме не так много точек. Это говорит о том, что для каждого узла спроса можно просто выполнить итерацию по всем исходным узлам и найти ближайший.

Возможно это:

def distance(a, b):
    return sum((xa - xb) ** 2 for (xa, xb) in zip(a, b))

def clusters(sources, demands):
    result = dict((source, []) for source in sources)
    for demand in demands:
        nearest = min(sources, key=lambda s: distance(s, demand))
        result[nearest].append(demand)
    return result

Этот код даст вам словарь, отображающий исходные узлы в список всех узлов спроса, которые находятся ближе к этому исходному узлу, чем любой другой.

Это не особенно эффективно, но очень просто!

Answer 4

Я думаю, что ответ по пространственному индексу по wye.bee (например, kd-дерево) является самым простым решением вашей проблемы.

Кроме того, вы также спросили, есть ли более простая альтернатива алгоритму Фортуны, и на этот конкретный вопрос я вам отвечаю: самый простой алгоритм реализации диаграммы Вороного?

Answer 5

Запустите этот код в Mathematica. Это впечатляюще! (Да, я знаю, что это не Python, но...)

pts3 = RandomReal[1, {50, 3}];
ListDensityPlot[pts3, 
    InterpolationOrder -> 0, ColorFunction -> "SouthwestColors", Mesh -> All]

Answer 6

Вы не сказали, почему хотели избежать алгоритма Фортуны. Я предполагаю, что вы имели в виду, что вы просто не хотели реализовывать это самостоятельно, но это уже было реализовано в сценарии Биллом Саймонсом и Карстоном Фармером, поэтому вычисление диаграммы вороного не должно быть сложным.

Основываясь на их сценарии, я сделал его еще проще в использовании и загрузил его в PyPi под именем Pytess. Таким образом, вы можете использовать функцию pytess.voronoi(), основанную на синих точках, в качестве входных данных, возвращая исходные точки с их вычисленными полигонами вороной. Затем вам нужно будет назначить каждую черную точку с помощью тестирования точки в полигоне, которое вы можете использовать на http://geospatialpython.com/2011/08/point-in-polygon-2-on-line.html.