Описание тега lcs

Источник: http://en.wikipedia.org/wiki/Longest_common_subsequence_problem

О

lcs или самой длинной общей подпоследовательности - это проблема при поисковой оптимизации: для заданных двух строк найти общую подпоследовательность в данных строках с максимальной длиной. Задача может быть решена за полиномиальное время с использованием подхода динамического программирования. Алгоритм решения этой проблемы является рекурсивным и дает следующую рекурсивную формулу.

Если i == 0 или j == 0, то C[i][j] = 0
   Если i,j > 0 и x _i == y _i,                      то C[i][j] = c[i-1,j-1]+1
   Если i,j > 0 и x _i! = Y _i,                       то C[i][j] = max(c[i,j-1],c[i-1,j ])

Псевдокод

 p = A.length
 q = B.length
 for i = 1 to p
     c[i,0] = 0
 for i = 1 to q
     c[0,j] = 0
 for i = 1 to p
     for j = 1 to q
          if i ==0 or j == 0
              c[i][j] = 0
          else if(A[i] == B[j] ) 
              c[i][j] = c[i-1][j-1] + 1; 
          else 
              if(c[i][j-1]>c[i-1][j])
                   c[i][j] = c[i][j-1];
              else
                   c[i][j] = c[i-1][j];
  return c

заявка

В биоинформатике сравнение двух цепей ДНК и сходство в этих цепях осуществляется с помощью этого алгоритма путем вычисления самой длинной общей подпоследовательности.

пример

• A = ATGCGTCGAT
• B = ATGTGACTAG

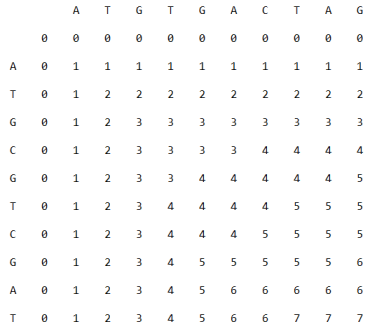
Самая длинная общая подпоследовательность состоит из 7 символов и это ATGTGAT.