График BER MATLAB калибровка
Я делаю 16QAM системы (передатчик, канал и приемник) и кривые BER и PER результатов. Однако у меня возникли некоторые проблемы с шумом в приемнике. Я запускаю систему в двух циклах: для всех значений Eb/No и для всех пакетов, и я отправил 200 символов и 1000 пакетов, но это все еще происходит. Я хотел бы проверить, является ли результат из этого кода правильным или нет:
clear all
clc
numPkts=1000;
N = 200; % number of symbols
M = 16; % constellation size
k = log2(M); % bits per symbol
pv=4; %prefix length
% defining the real and imaginary PAM constellation
% for 16-QAM
alphaRe = [-(2*sqrt(M)/2-1):2:-1 1:2:2*sqrt(M)/2-1];
alphaIm = [-(2*sqrt(M)/2-1):2:-1 1:2:2*sqrt(M)/2-1];
k_16QAM = 1/sqrt(10);
Eb_N0_dB = [0:15]; % multiple Es/N0 values
Es_N0_dB = Eb_N0_dB + 10*log10(k);
erTot=zeros(1,length(Eb_N0_dB));
% Mapping for binary <--> Gray code conversion
ref = [0:k-1];
map = bitxor(ref,floor(ref/2));
[tt ind] = sort(map);
for ii = 1:length(Eb_N0_dB)
for pktX=1:numPkts
% symbol generation
% ------------------
ipBit = rand(1,N*k,1)>0.5; % random 1's and 0's
ipBitReshape = reshape(ipBit,k,N).';
bin2DecMatrix = ones(N,1)*(2.^[(k/2-1):-1:0]) ; % conversion from binary to decimal
% real
ipBitRe = ipBitReshape(:,[1:k/2]);
ipDecRe = sum(ipBitRe.*bin2DecMatrix,2);
ipGrayDecRe = bitxor(ipDecRe,floor(ipDecRe/2));
% imaginary
ipBitIm = ipBitReshape(:,[k/2+1:k]);
ipDecIm = sum(ipBitIm.*bin2DecMatrix,2);
ipGrayDecIm = bitxor(ipDecIm,floor(ipDecIm/2));
% mapping the Gray coded symbols into constellation
modRe = alphaRe(ipGrayDecRe+1);
modIm = alphaIm(ipGrayDecIm+1);
% complex constellation
mod = modRe + j*modIm;
s1 = k_16QAM*mod; % normalization of transmit power to one
s=[s1(length(s1)-pv+1:end) s1]; %add prefix
% noise
% -----
EsNo=10^(Es_N0_dB(ii)/10);
stanDevNoise=sqrt((1)/(2*EsNo));
n =stanDevNoise *[randn(1,length(s)) + j*randn(1,length(s))]; % white guassian noise, 0dB variance
h=(1/sqrt(2))*(randn+j*randn);
y1= conv(s,h) + n; % additive white gaussian noise
%removes prefix
y1(1:pv) = [];
y=y1/h;
% demodulation
% ------------
y_re = real(y)/k_16QAM; % real part
y_im = imag(y)/k_16QAM; % imaginary part
% rounding to the nearest alphabet
ipHatRe = 2*floor(y_re/2)+1;
ipHatRe(find(ipHatRe>max(alphaRe))) = max(alphaRe);
ipHatRe(find(ipHatRe<min(alphaRe))) = min(alphaRe);
ipHatIm = 2*floor(y_im/2)+1;
ipHatIm(find(ipHatIm>max(alphaIm))) = max(alphaIm);
ipHatIm(find(ipHatIm<min(alphaIm))) = min(alphaIm);
% Constellation to Decimal conversion
ipDecHatRe = ind(floor((ipHatRe+4)/2+1))-1; % LUT based
ipDecHatIm = ind(floor((ipHatIm+4)/2+1))-1; % LUT based
% converting to binary string
ipBinHatRe = dec2bin(ipDecHatRe,k/2);
ipBinHatIm = dec2bin(ipDecHatIm,k/2);
% converting binary string to number
ipBinHatRe = ipBinHatRe.';
ipBinHatRe = ipBinHatRe(1:end).';
ipBinHatRe = reshape(str2num(ipBinHatRe).',k/2,N).' ;
ipBinHatIm = ipBinHatIm.';
ipBinHatIm = ipBinHatIm(1:end).';
ipBinHatIm = reshape(str2num(ipBinHatIm).',k/2,N).' ;
% counting errors for real and imaginary
nBitErr(pktX) = size(find([ipBitRe- ipBinHatRe]),1) + size(find([ipBitIm - ipBinHatIm]),1) ;
end
erTot(ii)=erTot(ii)+sum(nBitErr); %total errors in all packets
simBer(ii)=(erTot(ii)/(N*k*numPkts)); %bit error rate
totPktErRate(ii)=(erTot(ii)/(numPkts));
end
theoryBer = (1/k)*3/2*erfc(sqrt(k*0.1*(10.^(Eb_N0_dB/10))));
close all; figure
semilogy(Eb_N0_dB,theoryBer,'bs-','LineWidth',2);
hold on
semilogy(Eb_N0_dB,simBer,'mx-','LineWidth',2);
axis([0 15 10^-5 1])
grid on
legend('theory', 'simulation');
xlabel('Eb/No, dB')
ylabel('Bit Error Rate')
title('Bit error probability curve for 16-QAM modulation')
Спасибо!
1 ответ
Приведенный код делает следующие предположения:
- 16-QAM модуляция с использованием битового отображения с серым кодированием
- плоская медленная / блочная модель канала Рэлея с замиранием.
- когерентное декодирование при оценке информации о идеальном состоянии канала
Из-за его сходства с каналом Additive-White-Gaussian-Noise (AWGN) логическим первым шагом в понимании и калибровке производительности системы в соответствии с вышеизложенными допущениями является оценка ее производительности без затухания (то есть замена модели канала на AWGN). канал по настройке h=1 в предоставленном коде).
Канал AWGN
Вы можете захотеть проверить калибровку производительности Symbol-Error-Rate (SER), поскольку это может оказать большое влияние на производительность (BER), и кривые SER легко доступны для когерентного декодирования некодированного созвездия 16-QAM (см., Например, dsplog, эти слайды лекций, эта книга и т. д.) Эти ссылки также включают следующее приближение к SER 16-QAM:
1.5 * ERFC (SQRT (EsN0/10))
где EsN0 = 10.^(0.1*EsN0_dB),
Обратите внимание, что результаты могут быть эквивалентно представлены в терминах либо Es/N0 (средняя энергия на символ), либо Eb/N0 (средняя энергия на бит). Для созвездия сигнала k-битов (размер созвездия 2 k) соотношение между Es / N0 и Eb / N0 задается как
Es/N0 = k*Eb/N0
Таким образом, для 16-QAM Es/N0 = 4Eb/N0 (или Es / N0 дБ = Eb/N0 дБ + 6 дБ).
Для схемы с серым кодом приближение BER для достаточно высокого Eb / N0 может быть затем получено из того факта, что ошибка символа в большинстве случаев приводит к ошибке в 1 бит (из k-битов в символе), таким образом, BER ~ SER/k (или снова для 16-QAM: BER ~ SER/4).
Es/N0 (dB) Eb/N0 (dB) SER BER approx
15 9 1.8e-2 4.5e-3
16 10 7.0e-3 1.8e-3
18 12 5.5e-4 1.4e-4
20 14 1.2e-5 3.0e-6
25 19 2.7e-15 6.7e-16
В качестве примечания следует, что доверительный интервал результатов моделирования с использованием 2 000 000 символов при значениях SER ниже примерно 10 -5 может стать весьма значительным. В качестве иллюстрации следующий график показывает SER 16-QAM синим цветом с ожидаемым 95% -ным доверительным интервалом моделирования 2 000 000 символов красным цветом: 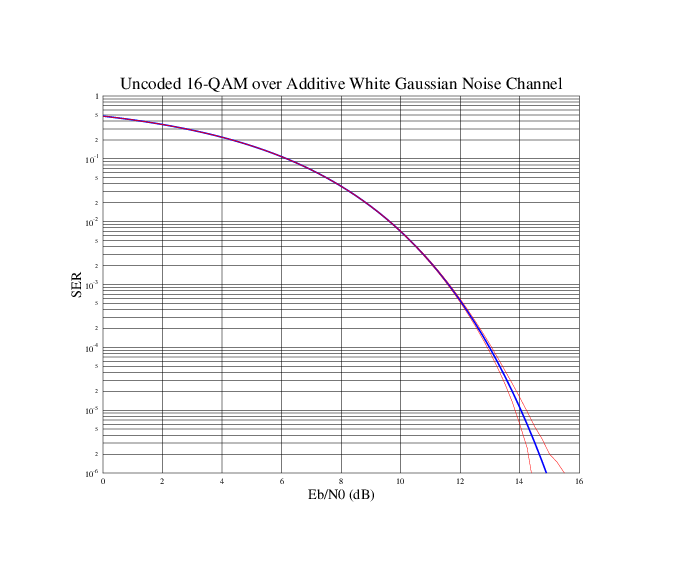
Релеевский блок затухания канала
Как только калибровка производительности была установлена для канала AWGN, мы можем вернуться к каналу замирания блока Рэлея, который используется в размещенном коде.
Предполагая точную оценку информации о состоянии канала в приемнике и, если бы не было шума, можно точно масштабировать принятый сигнал обратно на исходные передаваемые символы, используя преобразование:
у = у1 / ч;
Когда присутствует шум, это преобразование, к сожалению, также масштабирует шум. К счастью, шум остается белым и гауссовым, так что базовый вывод уравнений канала AWGN может быть повторно использован с некоторой работой. По независимым пакетам статистическое распределение масштабирования abs(h) следует распределению Рэлея (с параметром сигма 2 = 1/2). Таким образом, чтобы получить средний эффект этого масштабирования для SER, можно вычислить взвешенную сумму (где вес - функция плотности вероятности распределения Рэлея) эффектов во всем диапазоне возможных значений масштабирования, используя интеграл: 
Это можно сделать численно с помощью MATLAB, используя:
function SER = AwgnSer(EsN0)
SER = 1.5*erfc(sqrt(0.1*EsN0));
end
function f = WeightedAwgnSer(x)
weight = 2*x.*exp(-x.*conj(x));
f = weight*AwgnSer(EsN0*x.*conj(x));
end
function SER = BlockRayleighFadingSer(EsN0)
for ii=1:length(EsN0)
SER(ii) = quad(inline('WeightedAwgnSer(EsN0(ii),s)','s'), 0, inf);
end
end
Аналогичный вывод может быть получен для BER:
function BER = AwgnBer(EsN0)
x = sqrt(0.1*EsN0);
q1 = 0.5*erfc(x);
q3 = 0.5*erfc(3*x);
q5 = 0.5*erfc(5*x);
BER = (12*q1+8*q3-4*q5 - q1*(q1+q3-2*q5)+(q3-q5)*q5)/16;
end
function f = WeightedAwgnBer(x)
weight = 2*x.*exp(-x.*conj(x));
f = weight*AwgnBer(EsN0*x.*conj(x));
end
function SER = BlockRayleighFadingBer(EsN0)
for ii=1:length(EsN0)
SER(ii) = quad(inline('WeightedAwgnBer(EsN0(ii),s)','s'), 0, inf);
end
end
Обратите внимание, что я использую точную формулу для BER, так как на средневзвешенное значение обычно влияет низкое отношение сигнал / шум, когда приближение не очень хорошее. Это не имеет большого значения для кривой (~0,3 дБ при Eb/N0=10 дБ), но это не то, о чем я хочу беспокоиться при калибровке кривых производительности.
Это дает следующие кривые производительности: 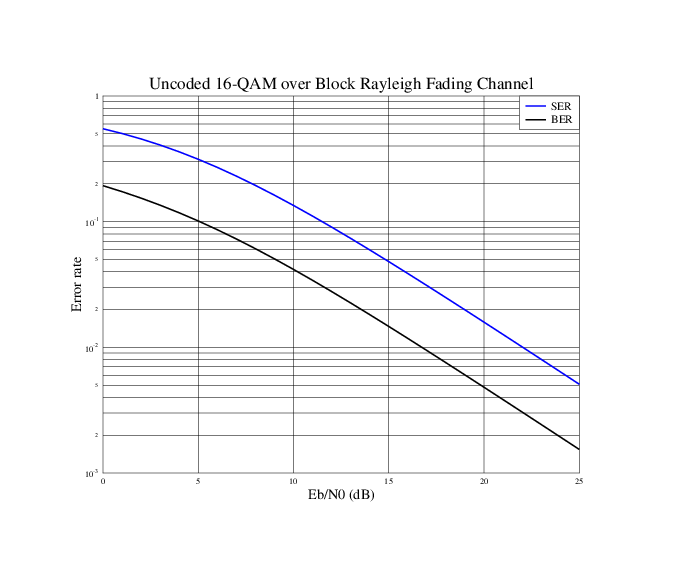
Другие соображения
На производительность декодирования может влиять ряд других факторов, которые выходят за рамки этого ответа. Таким образом, нижеследующее лишь кратко затрагивает несколько распространенных и ссылки на внешние ссылки, которые могут использоваться для получения дополнительной информации.
Декодер в размещенном коде использует явное знание эффекта замирания (как видно из строки y=y1/h;). Как правило, это не так, и сначала нужно оценить затухание. Оценка эффекта канала в приемнике выходит за рамки этого ответа, но, как правило, несовершенная оценка приводит к некоторой потере производительности. Кривые производительности совершенных знаний часто используются в качестве практического ориентира для сравнения производительности при несовершенной оценке канала.
Канальное кодирование часто делается для улучшения производительности системы. Общие критерии, используемые для кодированной модуляции по каналу AWGN:
- Пропускная способность канала Шеннона
- Верхняя граница объединения (например, примечания к этим лекциям) и множество других границ, найденных в исследовательской литературе
- Некодированная производительность модуляции (которую мы вывели здесь)
Аналогично для кодированной модуляции по каналу Рэлея с замиранием в виде плоских блоков обычно используются следующие критерии:
- Вероятность выхода из строя (см. Раздел 5.4.1 этой книги)
- Некодированная производительность модуляции (которую мы вывели здесь)