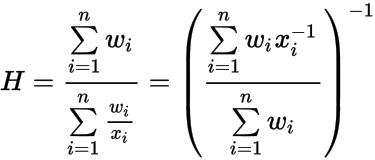Среднее гармоническое, когда присутствует сигнал постоянного тока
У меня есть выход из шумного сигнала, сохраненный в виде набора косинусов.
У меня есть набор частот от 0 в x Гц (х - большое число) и набор одинаковых размеров амплитуд.
Я хочу определить среднее гармоническое для частот, присутствующих, когда взвешивание частоты является величиной соответствующей амплитуды.
Например: если у меня есть набор частот[ 1 , 2 , 3] и амплитуды [ 10, 100, 1000 ] (такой, что косинус с частотой 1 имеет амплитуду 10, так далее.). Тогда среднее гармоническое частот 2.8647,
Тем не менее, я сталкиваюсь с проблемами, когда у меня нулевая частота (компонент "DC") - среднее значение гармоники равно нулю!
Проблема реальной жизни - очень большой набор косинусов, начиная с нулевой частоты и доходя до нескольких ГГц. Большая часть сигнала взвешена в части спектра, и я хочу сравнить простое взвешенное среднее спектра с гармоническим средним.
Способ обойти это (кажется дешевым способом) - игнорировать нулевую частоту - это только одна частота из десятков тысяч. Но есть ли правильный способ сделать это?
1 ответ
Ниже приведено уравнение для взвешенного среднего гармонического:
Применительно к вашему примеру это:
x = 1:3;
w = logspace(1,3,3); % [10 100 1000]
sum(w)/sum(w./x); % 2.8220
Вы можете увидеть, что если один из x значения 0сумма в знаменателе будет бесконечной. Если вы вручную установите вес этого значения в 0, вы бы 0/0 Сценарий в нижней сумме (которая оценивает NaN). Технически говоря - вы не можете иметь x из 0 в вычислении этого типа среднего без получения результата 0,
Я думаю, что совершенно ясно, что это не тот инструмент для обработки сигнала постоянного тока. Несколько вещей приходят на ум, чтобы получить значимую информацию:
- Разумно игнорировать сигнал постоянного тока обоими способами.
- Возможно, вам было бы лучше игнорировать его для целей гармонического среднего и добавить его впоследствии для совместимости с простым средним.
В конце дня вам нужно решить, что вы хотите сказать, и затем обработать данные соответствующим образом.